Into Math Grade 7 Module 11 Lesson 2 Answer Key Derive and Apply Formulas for Surface Areas of Cubes and Right Prisms

We included HMH Into Math Grade 7 Answer Key PDF Module 11 Lesson 2 Derive and Apply Formulas for Surface Areas of Cubes and Right Prisms to make students experts in learning maths.

HMH Into Math Grade 7 Module 11 Lesson 2 Answer Key Derive and Apply Formulas for Surface Areas of Cubes and Right Prisms

I Can derive and apply the formulas for surface area of any right prism.

Spark Your Learning

Sara is wrapping a gift box with dimensions 10 inches by 14 inches by 5 inches with wrapping paper. What is the least amount of wrapping paper she will need to cover the gift box without any overlap?

Answer:
520 in²
Explanation:
Dimensions: l = 10 inches, w = 14 inches, h = 5 inches
Surface area: A
A = 2(l x w + w x h x h x l)
A = 2(10×14 + 14×5 + 5×10)
A = 2(140 + 70 + 50)
A = 2(260)
A = 520 in²

Turn and Talk What is the difference between area and surface area?
Answer:
180 inches
Explanation:
Surface area: A
A = 2(l x w + w x h x h x l)
A = 2(10×14 + 14×5 + 5×10)
A = 2(140 + 70 + 50)
A = 2(260)
A = 520 in²
Volume: V = (l).(w).(h)
V = 10 x 14 x 5 = 700 in³

Build Understanding

Question 1.
A wooden toy box is represented by the net shown with it.

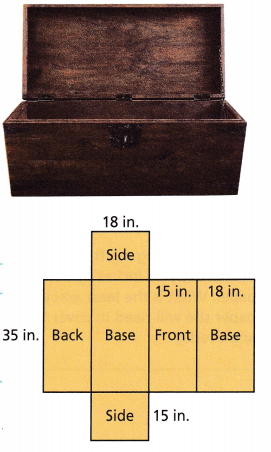
A. How many faces make up the toy box? What does the net show about these faces?
Answer:
6 faces

B. Are any of the faces congruent? If so, which ones?
Answer:
Base and base are congruent
Front and Back are congruent

C. What is the shape of the two bases? What is their combined area?
Answer:
Rectangle

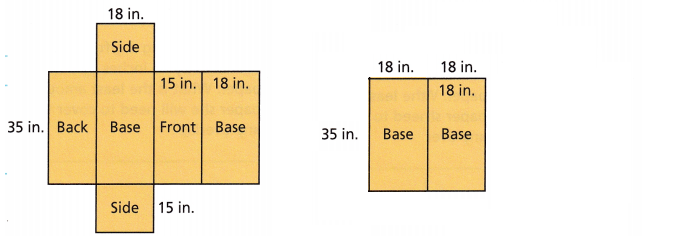
Combined area
A = Length x width
A = (18+18) x 35
A = 36 x 35
A = 1236 in²

D. What is the combined area of the front and back faces?
Answer:
1050 in²
Explanation:
Area A = length x width
A = 2(15 x 35 )
A = 2(525) = 1050 in²

E. What is the combined area of the left and right faces?
Answer:
540 in²
Explanation:
Area A = length x width
A = 2(15 x 18 )
A = 2(270) = 540 in²

F. How can you find the total surface area of the toy box? What is this value?
Answer:
2850 in²
Explanation:
Dimensions: l = 35 inches, w = 15 inches, h = 18 inches
Surface area: A
A = 2(l x w + w x h x h x l)
A = 2(35 × 15 + 15 x 18 + 18 x 35)
A = 2(525 + 270 + 630)
A = 2(1425)
A = 2850 in²

G. Use the net to derive a formula for surface area of a box with length l, width w, and height h:

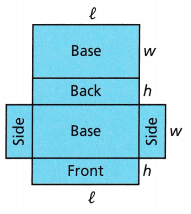
Surface area = 2lw + +
Since lw is the area of a _________, replace lw with B: 2B + 2lh + 2wh.
Both parts of the expression 2lh + 2wh contain an h, so factor it out: 28 + h( + ).
Since 2l + 2w represents the ____________ of the base, replace 2l + 2w with P:
Surface Area = 2B + h
Answer:
Surface area = 2lw + 2wh + 2hl
Since lw is the area of a Base, replace lw with B: 2B + 2lh + 2wh.
Both parts of the expression 2lh + 2wh contain an h, so factor it out: 2B + h(2l + 2w).
Since 2l + 2w represents the P of the base, replace 2l + 2w with P:
Surface Area = 2B + Ph

Turn and Talk How could you change the surface area formula for a cube to make it simpler?
Answer:
6s²
Explanation:
s is the side of a cube.
Surface area cube of same length, width and height= 2sxs + 2sxs + 2sxs = 6s²
Surface area = 2lw + 2wh + 2hl
l = s, w = s, h = s
Since s x s is the area of a Base, replace s x s with B: 2B + 2s.s + 2s.s.
Both parts of the expression 2s.s + 2s.s contain an h, so factor it out: 2B + s(2s + 2s).
Since 2s+ 2s represents the P of the base, replace 2s + 2s with P:
Surface Area = 2s.s + Ps
Step It Out

The surface area of a right prism is S = 2B + Ph, where B is the base area, P is the base perimeter, and h is the height of the prism.

Question 2.
A foundation has the water bottles shown as giveaways for its annual fundraiser. What is the approximate surface area of the water bottle, treating the top surface as flat and ignoring the spout?

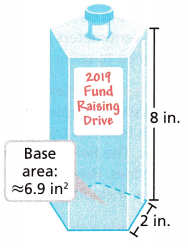
A. From the picture, the area of the base is approximately square inches and the height is inches.
The perimeter of the base is × = inches.
Answer:
A. From the picture, the area of the base is approximately 6.9 square inches and the height is 8 inches.
The perimeter of the base is 2 × 5 = 10 inches.
Explanation:
The surface area of a right prism is S = 2B + Ph, where B is the base area, P is the base perimeter, and h is the height of the prism
B= 6.9 sq in
The perimeter of the base is 2 × 5 = 10 inches.

B. Find the approximate surface area.
S = 2B + Ph
S = 2 + ()
S = +
S =
The surface area of the water bottle is approximately square inches.
Answer:
S = 2B + Ph
S = 2 (6.9) + 10 (8)
S = 13.8 + 80
S = 93.8 square inches.
The surface area of the water bottle is approximately 94 square inches.
Explanation:
Given, base = 6.9; perimeter = 10; height = 8
S = 2B + Ph
S = 2 (6.9) + 10 (8)
S = 13.8 + 80
S = 93.8 square inches.

Check Understanding

Question 1.
A couch cushion needs to be covered with fabric. The dimensions of the cushion are 1.5 feet long by 1.5 feet wide by 0.5 foot high. What is the least amount of fabric that will be needed to cover the couch cushion?
Answer:
7.5 in²
Explanation:
length 1.5 feet, width 1.5 feet and height = 0.5 feet
Surface area: A
A = 2(l x w + w x h x h x l)
A = 2(1.5×1.5 + 1.5 x 0.5 + 0.5×1.5)
A = 2(2.25 + 0.75 + 0.75)
A = 2(3.75)
A = 7.5 in²

Question 2.
Bobby is sanding a five-sided storage chest with the dimensions shown. The base is a regular pentagon. If he sands only the outside of the chest, approximately how much area must he sand?

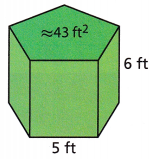
Answer:
236 square feet.
Explanation:
The surface area of a right prism is S = 2B + Ph,
where B is the base area, P is the base perimeter, and h is the height of the prism.
P = perimeter of base = 5×5 = 25
B area of base = 43sq ft
S = 2B + Ph
S = 2 (43) + 25 (6)
S = 86 + 150
S = 236 square feet.

Question 3.
A photographer’s darkroom needs a new coat of black paint on all surfaces of the room, including the ceiling and the floor. The room is a cube with edge length 11 feet. How much surface area must be painted?
Answer:
726 sq ft
Explanation:
6 s x s = 6 (11 x 11) = 6 x 121 = 726 sq ft
or
B= 121 sq ft
P = 44 ft
S = 2B + Ph
S = 2 (121) + 44 (11) = 242 + 484 = 726 sq feet

On Your Own

Question 4.
Lily is using wrapping paper to cover a box with dimensions 7 centimeters by 10 centimeters by 5 centimeters. What is the least amount of paper Lily will need to cover the box?
Answer:
310 square cm.
Explanation:
The surface area of a rectangular prism is S = 2B + Ph,
where B is the base area, P is the base perimeter, and h is the height of the prism.
length l = 7cm, width w = 10 cm and height h = 5 cm
P = perimeter of base = 2(7+10) = 34 cm
B area of base = 7 x 10 = 70 sq cm
S = 2B + Ph
S = 2 (70) + 34 (5)
S = 140 + 170
S = 310 square cm.

Question 5.
Use Structure Gavin is making a scale replica of a tent for his social studies project. The replica is in the shape of a triangular prism. It has an isosceles triangle base with side lengths 6 inches, 5 inches, and 5 inches. The height of the triangle is 4 inches, and the depth of the tent is 7 inches. How much fabric will Gavin need to make the outside of the replica, including the “floor”?
Answer:
88 square in.
Explanation:
The surface area of a triangular prism is S = 2B + Ph,
where B is the base area, P is the base perimeter, and h is the height of the prism
h= 4in; P = perimeter of base = 6 + 5 + 5 = 16 in
B area of base = 1/2(4 x 6) = 12 sq in
S = 2B + Ph
S = 2 (12) + 16 (4)
S = 24 + 64
S = 88 square in.

Question 6.
Blake made a storage bin out of poles in the shape of a regular hexagonal prism, as shown. He wants to cover the surface area of the prism, including the floor, with a tarp to protect his things from the weather. What is the approximate surface area that the tarp will cover? Explain.

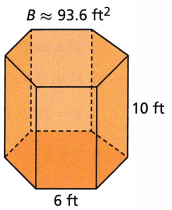
Answer:
547.2 square feet.
Explanation:
The surface area of a regular hexagonal prism is S = 2B + Ph,
where B is the base area, P is the base perimeter, and h is the height of the prism
P = perimeter of base = 6 x 6 = 36sq feet
B area of base = 93.6sq ft
S = 2B + Ph
S = 2 (93.6) + 36 (10)
S = 187.2 + 360
S = 547.2 square feet.

Find the surface area of each prism.

Question 7.

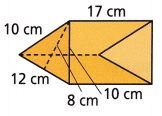
Answer:
352 square cm.
Explanation:
The formula for the surface area of triangular prism is:
Surface area = (Perimeter of the base × Length of the prism) + (2 × Base Area)
SA = (S₁ +S₂ + S₃)L + bh
P = perimeter of base = 12+10+10 = 32 cm
B area of base = (8×6) = 48 sq cm
S = 2B + Ph
S = 2 (48) + 32 (8)
S = 96 + 256
S = 352 square cm.

Question 8.

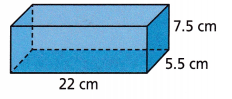
Answer:
924 square cm.
Explanation:
The surface area of a rectangular prism is S = 2B + Ph,
where B is the base area, P is the base perimeter, and h is the height of the prism
length l = 22cm, width w = 5.5 cm and height h = 7.5 cm
P = perimeter of base = 2(22+5.5) = 242 cm
B area of base = 22×10 = 220 sq cm
S = 2B + Ph
S = 2 (220) + 242 (7.5)
S = 440 + 484
S = 924 square cm.

Question 9.

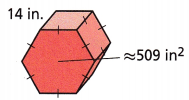
Answer:
2194 sq in
Explanation:
B= 509 sq in
P = 6 x 14 =84 in
S = 2B + Ph
S = 2 (509) + 84 (14)
= 1018 + 1176 = 2194 sq in

Question 10.

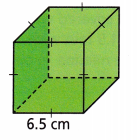
Answer:
253.5 sq cm
Explanation:
B= 6.5 x 6.5 = 42.25 sq cm
P = 4 x 6.5 = 26 cm
S = 2B + Ph
S = 2 (42.25) + 26 (6.5) = 84.5 + 169 = 253.5 sq cm
or
6 x side x side = 6 x 6.5 x 6.5 = 253.5 sq cm

I’m in a Learning Mindset!

How does using the formulas for surface area of right prisms help me find surface area more efficiently?
Answer:
Surface area = Bl + Ph
B base area and L is length
P is the perimeter of the base
h is the height of the triangle
the formulas for surface area of right prisms help me find surface area more efficiently and easy

Lesson 11.2 More Practice/Homework

Question 1.
Use Structure Melissa baked a cake. The box for the cake is ¡n the shape of a cube with edges 9 centimeters in length. Draw a supporting picture and find how many square centimeters of cardboard are needed to make the box.

Answer:
486 sq cm
Explanation:
B= 9 x 9 = 81 sq cm
P = 4 x 9 = 36 cm
S = 2B + Ph
S = 2 (81) + 36 (9) = 162 + 324 = 486 sq cm
or
6 x side x side = 6 x 9 x 9 = 486 sq cm

Question 2.
Sue is upholstering a rectangular ottoman that measures 21 centimeters by 18 centimeters by 15 centimeters. What will be the total square centimeters of fabric that Sue must use to cover all faces of the ottoman?
Answer:
1926 square cm.
Explanation:
The surface area of a rectangular prism is S = 2B + Ph,
where B is the base area, P is the base perimeter, and h is the height of the prism
length l = 21cm, width w = 18 cm and height h = 15 cm
P = perimeter of base = 2(21 + 18) = 2 x 39 = 78 cm
B area of base = 21 x 18 = 378 sq cm
S = 2B + Ph
S = 2 (378) + 78 (15)
S = 756 + 1170
S = 1926 square cm.

Question 3.
A drawing of the attic in a house is shown. It needs insulation on all sides. How many square feet of insulation are needed?

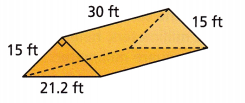
Answer:
1761 ft²
Explanation:
Surface area = (Perimeter of the base × Length of the prism) + (2 × Base Area)
SA = (S₁ +S₂ + S₃)L + bh
P = perimeter of base = 21.2 + 15 + 15 = 51.2 ft
B area of base = (15 x 15) = 225 ft²
SA = (S₁ +S₂ + S₃)L + bh
SA = 51.2 x 30 + 225
S = 1536 +225 = 1761 ft²

For Problems 4-7, find the surface area of each prism. Round to the nearest tenth if necessary.

Question 4.
Math on the Spot

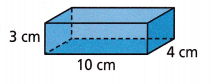
Answer:
164 square cm.
Explanation:
The surface area of a rectangular prism is S = 2B + Ph,
where B is the base area, P is the base perimeter, and h is the height of the prism
length l = 10 cm, width w = 4 cm and height h = 3 cm
P = perimeter of base = 2(10 + 4) = 2 x 14 = 28 cm
B area of base = 10 x 4 = 40 sq cm
S = 2B + Ph
S = 2 (40) + 28 (3)
S = 80 + 84
S = 164 square cm.

Question 5.

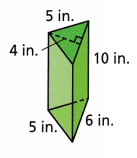
Answer:
84 sq cm
Explanation:
The formula for the surface area of triangular prism is:
Surface area = (Perimeter of the base × Length of the prism) + (2 × Base Area)
SA = (S₁ +S₂ + S₃)L + bh
P = perimeter of base = 5 + 5 + 6 = 16 cm
B area of base = (4×3) = 12 sq cm
S = 2B + Ph
S = 2 x12 + 16 x 4
S = 24 + 64
S = 84 sq cm
Question 6.
Regular pentagon base 7.
B ≈ 61.94 cm²

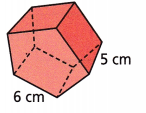
Answer:
273.88 cm²
Explanation:
B = 61.94 cm²
P = 6 x 5 = 30 cm
S = 2B + Ph
S = 2 (61.94) + 30 (5)
= 123.88 + 150 = 273.88 cm²

Question 7.

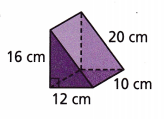
Answer:
672 cm²
Explanation:
Surface area = (Perimeter of the base × Length of the prism) + (2 × Base Area)
SA = (S₁ +S₂ + S₃)L + bh
P = perimeter of base = 16 + 12 + 20 = 48 cm
B area of base = (16 x 12) = 192 cm²
SA = (S₁ +S₂ + S₃)L + bh
SA = 48 x 10 + 192
S = 480 +192 = 672 cm²
Test Prep

Question 8.
Find the surface area of the figure.

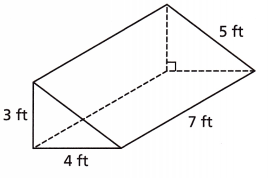
(A) 41 ft²
(B) 69 ft²
(C) 75 ft²
(D) 96 ft²
Answer:
Option(D)
Explanation:
Base = 4; height = 3; length = 7
Surface Area = 2(4×3)/2 + (4×7) + (3×7)+ 7×5
= 12 + 28 + 21 + 35 = 96 ft²

Question 9.
Mark bought a jewelry box in the shape of a cube. The jewelry box has edge lengths of 6 inches. What is the total surface area of the jewelry box?
(A) 36 in²
(B) 108 in²
(C) 216 in²
(D) 1,296 in²
Answer:
Option (C)
Explanation:
Surface area of cube = 6 x side x side
= 6 x 6 x 6 = 216 in²

Question 10.
Find the surface area of a rectangular prism with length of 4.7 inches, width of 6.4 inches, and height of 8.2 inches. Round to the nearest tenth.
Answer:
242.2 in²
Explanation:
length 4.7 inches, width of 6.4 inches, and height of 8.2 inches
Surface area: A
A = 2(l x w + w x h x h x l)
A = 2(4.7 x 6.4 + 6.4 x 8.2 + 8.2 x 4.7)
A = 2(30.08 +52.48 + 38.54)
A = 2(121.1)
A = 242.2 in²

Question 11.
Find the surface area of a regular hexagonal prism with side length 4.2 millimeters, height 3.9 millimeters, and base area of approximately 45.8 square millimeters. Round to the nearest tenth.
Answer:
189.88 square millimeters.
The surface area of a regular hexagonal prism is S = 2B + Ph, where B is the base area,
P is the base perimeter, and h is the height of the prism
P = perimeter of base = 6 x 4.2 = 25.2 square millimeters
B area of base = 45.8 square millimeters
height = 3.9 millimeters
S = 2B + Ph
S = 2 (45.8) + 25.2 (3.9)
S = 91.26 + 98.28
S = 189.88 square millimeters.

Spiral Review

Question 12.
Identify the two-dimensional figure that results from slicing a cylinder parallel to its base.

Answer:
Rectangle

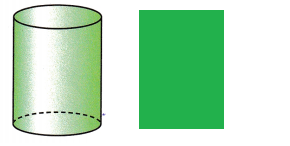
Explanation:
When the two-dimensional figure slice a cylinder parallel to its base the result is recctangle.

Question 13.
Find the area of the composite figure.

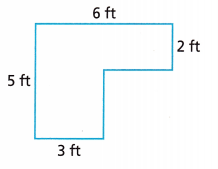
Answer:
21 sq ft
Explanation:

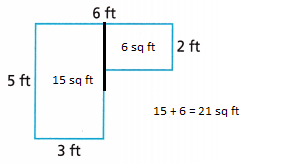
5 x 3 = 15 sq ft
2 x 3 = 6 sq ft
total surface area = 15 + 6 = 21 sq ft