Into Math Grade 7 Module 11 Lesson 3 Answer Key Derive and Apply a Formula for the Volume of a Right Prism

We included HMH Into Math Grade 7 Answer Key PDF Module 11 Lesson 3 Derive and Apply a Formula for the Volume of a Right Prism to make students experts in learning maths.

HMH Into Math Grade 7 Module 11 Lesson 3 Answer Key Derive and Apply a Formula for the Volume of a Right Prism

I Can accurately apply the formula to find the volume of right prisms.

Spark Your Learning

Use unit cubes or graph paper to find how many 1-inch cubes could fit into a rectangular prism with edge lengths shown. Describe how you found your answer.

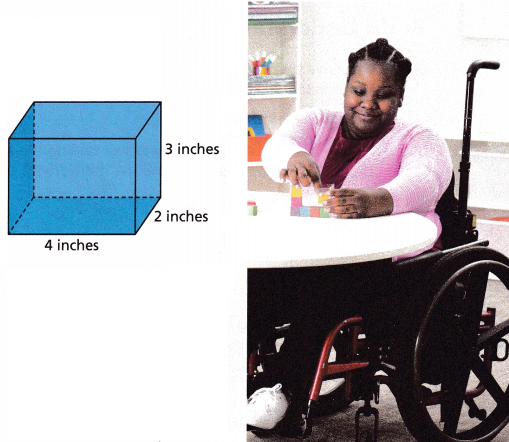
Answer:
24 inches
Explanation:
The volume is found using the formula:
Volume = Length × Width ×  Height
Which is usually shortened to:
V = l × w × h
V = 4 x 2 x 3 = 24
24 numbers of 1-inch cubes could fit into a rectangular prism

Turn and Talk How are the dimensions of the box related to the number of unit cubes required to fill it?
Answer:
Total volume size is calculated first, then sub dividing the total volume by the unit cube shows the number of unit cubes required to fill it.

Build Understanding

Question 1.
To derive the formula for volume of any right prism, imagine filling a right rectangular prism with 1-inch cubes.

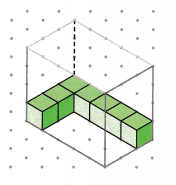
A. How many 1-inch cubes can be placed along the length of the prism shown here? The width of the prism?
Answer:
1-inch cubes can be placed along the length is 5
1-inch cubes can be placed along the width is 3
Explanation:
Count the cubes of the length to find the width of the prism.

B. How many cubes are needed to make one horizontal layer in the prism? Explain how you found your answer.
Answer:
15 cubes are needed to make one horizontal layer in the prism
Explanation:
Horizontal prism = length x width
length = 5; width = 3
p = 5 x 3 = 15 cubes

C. How is completing the first layer like finding the area of a rectangle or a cross-section of the prism? How is it different?
Answer:
1-inch cubes can be placed along the length is 5
1-inch cubes can be placed along the width is 3
Explanation:
area = length x width
area = 5 x 3 = 15

D. How will the number of cubes needed to make the first layer compare to the number of cubes needed to complete any other layer?
Answer:
15 cubes
Explanation:
area = length x width
area = 5 x 3 = 15
by placing each cube of one unit in each place
15 cubes can fill the first layer

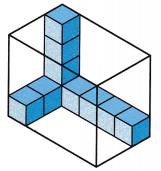
E. How many layers will it take to fill the prism shown? How did you find your answer?

Answer:
4 layers
Explanation:
There are 4 cubes can be placed vertically as layer by layer, then it require 4 layers to fill the prism.

F. Using the concept of “layers,” how can you determine the number of cubes it will take to fill up the entire volume of the prism? What is the volume of the prism?
Answer:
volume of the prism = total number of layers x the cubes in the each layer

G. Using Parts A through F, complete the statements to derive the formula for the volume V of a right prism.
V = (length × __________) × _____________
V = area of the __________ × _____________
Answer:
V = (length × width) × height
V = area of the rectangle × height

Turn and Talk Using what you know about the formulas for area of triangles and trapezoids, will this same formula work for other types of prisms?
Answer:
Yes, the formulas for area of triangles and trapezoids have the same formula work for other types of prisms.
Explanation:
Trapezoid has bases a and b, and the altitude h.
Its area is (a + b/2) x h
parallelogram: a = b => area is (a + a/2) x h = a x h
Triangle: b = 0, => area is 1/2 (a x h)

Step It Out

The formula for volume, V = Bh, is the area of the base (b) of a prism multiplied by its height (h).

Question 2.
Find the volume of the tent shown.

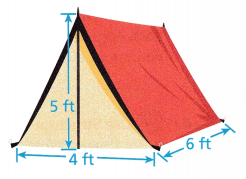
A. Since the tent is shaped like a prism, the base of the prism is a (triangle / rectangle).
Answer:
Triangle
Explanation:
A triangle is a three-sided polygon that consists of three edges and three vertices.

B. Write an expression for the area of the base of the prism.
B = () () ()
Answer:
B = 1/2 x Base x Height
Explanation:
The formula for the surface area of a prism is obtained by taking the sum of twice the base area and the lateral surface area of the prism.
The surface area of a prism is given as S = (2 × Base Area) + (Base perimeter × height) where “S” is the surface area of the prism.

C. The length of the tent is feet. This represents the (base / height) of the prism.
Answer:
length = 6 feet
height of the prism

D. Use the formula.
V = Bh
V = ( • • ) = ft³
Answer:
60 ft³
Explanation:
V = (1/2 x 4 x 5 ) x 6
V = 10 x 6
V = 60 ft³

Question 3.
A hexagonal prism has a volume of 60 cubic centimeters. The hexagonal base has an area of 12 square centimeters. Find the height of the prism.

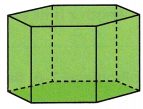
A. The base of this prism is a (hexagon / rectangle).
Answer:
Hexagon
Explanation:
A hexagon can be defined as a closed two-dimensional polygon with six sides.
Hexagon has 6 vertices and 6 angles also.

B. Use the formula.
V = Bh
= h
= h
The height of the hexagonal prism is centimeters.
Answer:
5 cm
Explanation:
60 = 12 h
dividing by 12 on both sides
60 : 12 = h
h = 5 cm
The height of the hexagonal prism is 5 centimeters.

Check Understanding

Question 1.
A rectangular sandbox measures 4 feet by 7 feet by 2 feet. How many cubic feet of sand can the sandbox hold?
Answer:
56 cubic feet
Explanation:
V =length x width x height
V = Bh
V = (4×7)x2
V= 56 ft³

Question 2.
A triangular prism has a base length of 1.5 centimeters, a base height of 3 centimeters, and a height of 12 centimeters.
A. Find the volume of the prism.
Answer:
27cm³
Explanation:
V = Bh
V = (1/2 x 3 x 1.5 ) x 12
V = 2.25 x12
V = 27cm³

B. A pentagonal prism has the same volume as the triangular prism in Part A. Its base has an area of centimeters. Find its height.
Answer:
6 cm
Explanation:
V = 27 cm³
V = Bh
base area = (1/2 x 3 x 1.5 ) = 2.25 cm²
27 = 2.25 x h
dividing by 2.25 on both sides
27 : 2.25 = h
h = 6 cm

On Your Own

Question 3.
Leah is filling a cube-shaped box with packing material and gift items. Each edge length of the box is 20 inches. What is the greatest possible volume of all the presents and packing material inside the cube?
Answer:
8000 in³
Explanation:
V=Bh = (l x w) x h
V = 20 x 20 x 20 = 8000 in³

Question 4.
Use Structure A lantern is represented by the pentagonal prism shown. What is the area of the base of the lantern? Explain your reasoning. Round to the nearest tenth.

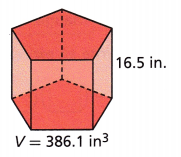
Answer:
23 sq in
Explanation:
V = Bh
386.1 = B x 16.5
dividing by 16.5 on both sides
386.1 : 16.5 = B
B = 23.4
Question 5.
A rectangular water tank can hold 142.5 cubic meters of water. Its base is 9.5 meters by 5 meters. What is its height?
Answer:
3 meters
Explanation:
V = 142.5 cu meters
B =9.5 x 5 = 47.5 sq meters
V = Bh
142.5 = 47.5 x h
dividing by 47.5 on both sides
47.5 : 142.5 = h
h = 3 meters

Question 6.
A triangular prism has the dimensions shown. What is the length x if its volume is 72 cubic feet?

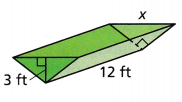
Answer:
4 ft
Explanation:
B = 1/2 x 3 x x
V = Bh
72 = 1/2 x 3 x x x 12
x = 72 /( 18) = 4 ft

For Problems 7-8, find the volume of each figure.

Question 7.

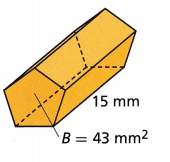
Answer:
645 mm³
Explanation:
V =Bh
V = 43 x 15
V = 645 mm³

Question 8.

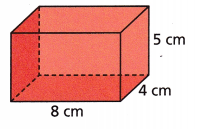
Answer:
160 cm³
Explanation:
V =Bh
V = (8 x 4) x 5
V = 160 cm³

I’m in a Learning Mindset!

Did I manage my time well when I applied the formulas for volumes of right prisms? What can I do to manage my time better?
Answer:
Yes, by using formulas to manage time in finding the Volume and area is better idea.
Explanation:
To find the volume of a rectangular prism, multiply its 3 dimensions: length x width x height.
The volume is expressed in cubic units.
Multiply the length, width and height to get the volume.

Lesson 11.3 More Practice/Homework

Question 1.
The Trust family rented the cabin shown in the shape of a triangular prism. The cabin is 30 feet deep. What is its volume?

Answer:
5625 ft³
Explanation:
V = Bh
V = (1/2 x 25 x 15) x 30
V = 187.5 x  30
V = 5625 ft³

Question 2.
A piece of copper tubing is in the shape of a hexagonal prism. The area of the base of the prism is 3 square centimeters. The volume of the prism is 51 cubic centimeters. What is the height of the tubing?
Answer:
17 cm
Explanation:
B = 3 sq cm
V = 51 cq cm
V = B h
51 = 3h
h = 51/3 = 17cm

Question 3.
Open-Ended A restaurant’s walk-in commercial refrigerator has a capacity of 120 cubic feet. It is a rectangular prism 6 feet tall. Using graph paper, model the possible dimensions of the length and width of the refrigerator’s footprint. (Hint: Have each square on the graph paper represent one square foot.) Are your answers reasonable? Explain.
Answer:
20 feet

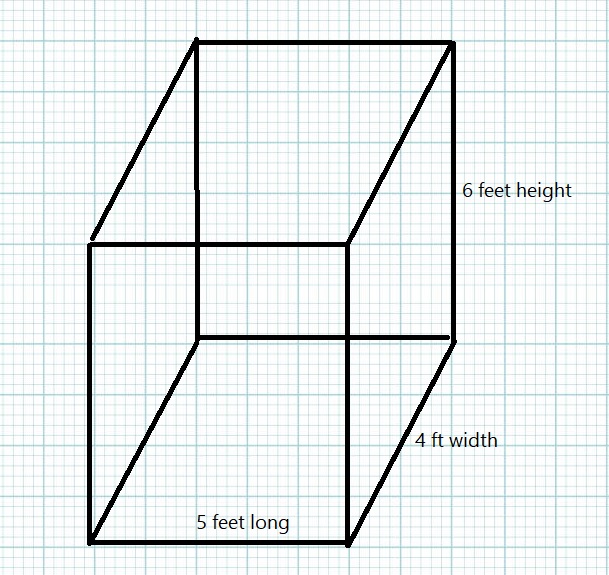
Explanation:
V = 120 cu ft
h = 6 ft
120 = 6 x l x b
l x b = 20
5 x 4 = 20

Question 4.
Math on the Spot Find the volume of the triangular prism.

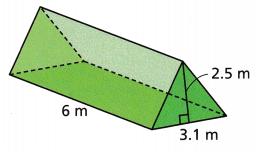
Answer:
23.25cq m
Explanation:
Volume = 1/2 Base x height
V = 1/2 (3.1 x 2.5) x 6
V = 3.875 x 6
V = 23.25sq m

Find the volume of each figure.

Question 5.

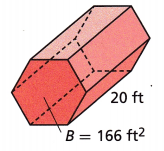
Answer:
3320 ft³
Explanation:
V = Bh
V = 166 x 20
V = 3320 ft³

Question 6.

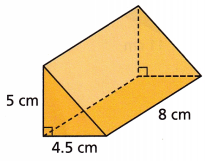
Answer:
90 cm³
Explanation:
V = Bh
V = (1/2 x 5 x 4.5) x 8
V = 11.25 x 8
V = 90 cm³

Test Prep

Question 7.
Jerome photographed an aquarium that measured 12 inches by 18 inches by 24 inches. Lim photographed an aquarium that was 12 inches by 30 inches by 12 inches. Both aquariums are rectangular prisms. How much more volume does Jerome’s aquarium have than Lim’s?
Answer:
864 cu in more volume does Jerome’s aquarium have than Lim’s
Explanation:
Jerome photographed an aquarium that measured 12 inches by 18 inches by 24 inches.
V = Bh = (lxw)xh
V = (12×18)x24
V = 216 x 24
V1 = 5184 cu inches
Lim photographed an aquarium that was 12 inches by 30 inches by 12 inches.
V = Bh = (lxw)xh
V = (12×30)x12
V = 360 x 12
V2 = 4320 cu inches
V = V1 – V2
V = 5184 – 4320 = 864 cu in
864 cu in more volume does Jerome’s aquarium have than Lim’s

Question 8.
An attic for a dollhouse is represented by a triangular prism with the dimensions shown. What is the volume of the attic?

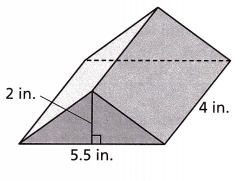
(A) 11.5 in³
(B) 22 in³
(C) 44 in³
(D) 88 in³
Answer:
Option(B)
Explanation:
V = Bh
V = (1/2 x 2 x 5.5) x 4
V = 22 in³

Question 9.
The volume of an octagonal prism is 1,260 cubic meters. The base has an area of 28 square meters. Write and solve an equation to find the height of the prism.
Answer:
45 mtrs
Explanation:
V = Bh
1260 = 28 h
h = 45 mtrs

Question 10.
A rectangular prism has a volume of 98 cubic feet, a width of 2 feet, and a length of 7 feet. Find the height of the rectangular prism.
Answer:
7ft
Explanation:
V = Bh
98 = 2×7 x h
h = 98/14
h = 7 ft

Spiral Review

Question 11.
Use geometry software to draw a quadrilateral with two pairs of parallel sides and four right angles. What is the quadrilateral?
Answer:
Square or Rectangle

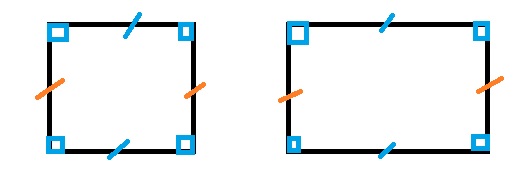
Explanation:
A quadrilateral with two pairs of parallel sides and four right angles is square or rectangle.
Square has four sides with four angles.
Rectangle has two pairs of parallel sides with four right angles.

Question 12.
Find the surface area of the right triangular prism.

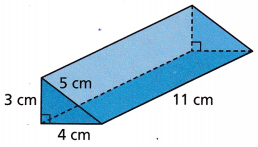
Answer:
198 sq cm
Explanation:
SA = Bh + Pl
SA = (1/2 x 3 x 4) x 11 + (4+3+5) 11
SA = 66 + 132
SA = 198 sq cm

Question 13.
Find the approximate surface area of the regular pentagonal prism.

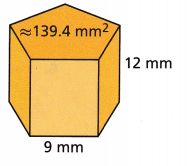
Answer:
2212.8 sq mm
Explanation:
SA = Bh + Pl
SA = 139.4 x 12 + 9×5 x 12
SA = 1672.8 + 540
SA = 2212.8 sq mm