Into Math Grade 6 Module 8 Lesson 4 Answer Key Interpret and Evaluate Algebraic Expressions

We included HMH Into Math Grade 6 Answer Key PDF Module 8 Lesson 4 Interpret and Evaluate Algebraic Expressions to make students experts in learning maths.

HMH Into Math Grade 6 Module 8 Lesson 4 Answer Key Interpret and Evaluate Algebraic Expressions

I Can interpret and evaluate algebraic expressions using the order of operations.

Step It Out

You can evaluate an expression with a variable by substituting a known value for the variable.

Question 1.
Evaluate each expression for the given value of the variable.

A. The area of a rug can be represented by the expression 6w.
Find the area when w = 4 feet.
Substitute 4 for w. 6()
Multiply.
When w = 4 ft, 6w = square feet.
Answer:
Given,
w = 4 feet
Now we have to substitute 4 for w.
Area of the rectangle = l × w
A = 6 × 4
6 × 4 = 24
When w = 4 ft, 6w = 24 square feet.

B. Evaluate 18y when y = \(\frac{2}{3}\).
Substitute \(\frac{2}{3}\) for y. 18
Multiply.
When y = \(\frac{2}{3}\), 18y = .
Answer:
Given,
18y when y = \(\frac{2}{3}\)
18 × \(\frac{2}{3}\) = 6 × 2 = 12
When y = \(\frac{2}{3}\), 18y = 12

C. Evaluate x – 12 when x = 18.6.
Substitute 18.6 for x. – 12
Subtract.
When x = 18.6, x – 12 = .
Answer:
x – 12 when x = 18.6
We have to substitute 18.6 for x.
18.6 – 12 = 6.6
x – 12 = 6.6

Turn and Talk For the expression in Part A. how is the value of the expression related to the value of the variable? Explain.
Answer:
The shape of the rug is in the form of a rectangle.
By seeing the figure we can say that the width is less than the length of the rug.
Area of the rectangle = l × w
A = 6 × 4
6 × 4 = 24
When w = 4 ft, 6w = 24 square feet.

Sometimes expressions have more than one variable.

Question 2.
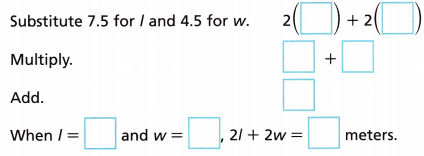
The perimeter of a rectangular swimming pool can be written as 2l + 2w, where l is the length and w is the width. Find the perimeter when l = 7.5 meters and w = 4.5 meters.


Answer:
Given,
l = 7.5 meters and w = 4.5 meters
The perimeter of a rectangular swimming pool can be written as 2l + 2w,
where l is the length and w is the width.
Substitute 7.5 for l and 4.5 for w.
P = 2(7.5 + 4.5)
P = 2 (12)
P = 24
Thus when l = 7.5 and w = 4.5, 2l + 2w = 24 meters

Question 3.
Evaluate each expression for the given values of the variables.
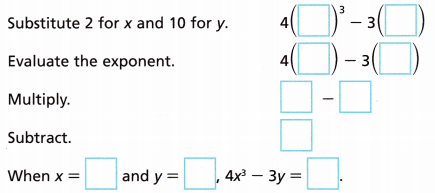
A. Evaluate 4x³ – 3y when x = 2 and y = 10.

Answer:
4x³ – 3y when x = 2 and y = 10
Substitute x = 2 and y = 10
4(2)³ – 3(10)
4(8) – 30
32 – 30 = 2
So, when x = 2 and y = 10, 4x³ – 3y = 2.

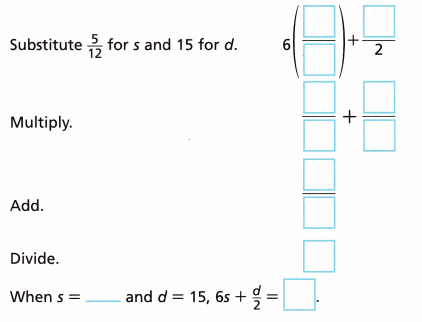
B. Evaluate 6s + \(\frac{d}{2}\) when s = \(\frac{5}{12}\) and d = 15.

Answer:
6s + \(\frac{d}{2}\)
when s = \(\frac{5}{12}\) and
d = 15
6 (\(\frac{5}{12}\)) + \(\frac{15}{2}\)
\(\frac{5}{2}\) + \(\frac{15}{2}\) = \(\frac{20}{2}\) = 10
So, when s = \(\frac{5}{12}\) and d = 15
6s + \(\frac{d}{2}\) = 10

Turn and Talk How is evaluating algebraic expressions similar to evaluating numerical expressions? How is it different? Explain.
Answer:

C. Evaluate 4x²y when x = 3 and y = 0.5.
Substitute 3 for x and 0.5 for y. 4()² ()
Evaluate the exponent. 4()()
Multiply.
When x = and y = 0.5, 4x²y = .
Answer:
4x²y when x = 3 and y = 0.5
Substitute 3 for x and 0.5 for y
4(3)².0.5 = 4(9) × 0.5
= 36 × 0.5
= 18
So, When x = 2 and y = 0.5, 4x²y = 18.

Question 4.
The expression 1 .8C + 32 gives the temperature in degrees Fahrenheit (°F) for a given temperature C in degrees Celsius (°C). Find the temperature in degrees Fahrenheit that is equivalent to 30 °C.

Substitute 30 for C. 1.8( ) + 32
Multiply. + 32
Add.
30°C = °F
Answer:
Substitute 30 for C.
1.8( 30) + 32
54 + 32 = 86
30°C = 86 °F

Check Understanding

Question 1.
Evaluate the expression \(\frac{6x}{5}\) when x = 20.

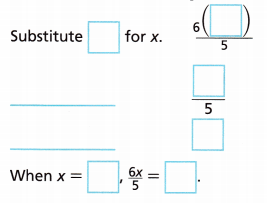
Answer:
\(\frac{6x}{5}\) when x = 20
\(\frac{6(20)}{5}\) = \(\frac{120}{5}\) = 60
So, when x = 20, \(\frac{6x}{5}\) = 60

Question 2.
The expression \(\frac{k}{8}\) shows the cost per person of splitting a restaurant bill k among 8 people. Evaluate the expression when k = 72 dollars.

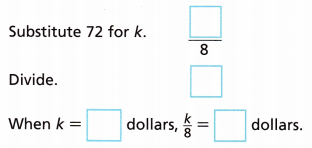
Answer:
Given,
The expression \(\frac{k}{8}\) shows the cost per person of splitting a restaurant bill k among 8 people.
Substitute 72 for k.
\(\frac{k}{8}\) = \(\frac{72}{8}\) = 9
So, when k = 72 dollars, \(\frac{k}{8}\) = 9

For Problems 3-6, evaluate the expression when x = 4 and y = 3.

Question 3.
3x – 4y
Answer:
Given,
3x – 4y, when x = 4 and y = 3
Substitute 4 for x and 3 for y
3(4) – 4(3) = 12 – 12 = 0
3x – 4y = 0

Question 4.
2x²
Answer:
Given,
2x²
when x = 4
Substitute 4 for x in 2x²
2 (4²) = 2 × 16 = 32
2x² = 32

Question 5.
\(\frac{30}{y}\)
Answer:
Given,
\(\frac{30}{y}\)
Substitute 3 for y
\(\frac{30}{y}\) = \(\frac{30}{3}\) = 10
So, \(\frac{30}{y}\) = 10

Question 6.
\(\frac{3x}{4y}\)
Answer:
Given,
\(\frac{3x}{4y}\)
Substitute 4 for x and 3 for y
\(\frac{3x}{4y}\) = \(\frac{3(4)}{4(3)}\) = \(\frac{12}{12}\) = 1
\(\frac{3x}{4y}\) = 1

On Your Own

Question 7.
The volume of a right rectangular prism is found by multiplying length by width by height, or lwh. What is the volume of a right rectangular prism with length 6 inches, width 4 inches, and height \(\frac{3}{4}\) inch?

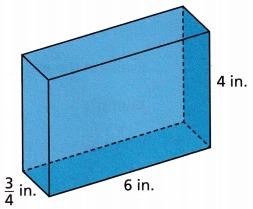
Substitute 6 for l, 4 for w, and \(\frac{3}{4}\) for h. (_______) (________) (_________)
Multiply. __________
Answer:
Given,
The volume of a right rectangular prism is found by multiplying the length by width by height, or lwh.
Substitute 6 for l, 4 for w, and \(\frac{3}{4}\) for h.
V = l . w . h
V = 6 × 4 × \(\frac{3}{4}\)
V = 6 × 3
V = 18 cubic in.

Question 8.
Jasper needs wood for a rectangular sandbox. The sandbox will be 8 feet by 4.5 feet. He knows the perimeter is found using the expression 2l + 2w, or 2(1 + w). How many feet of wood should Jasper use?
Answer:
Given,
Jasper needs wood for a rectangular sandbox.
The sandbox will be 8 feet by 4.5 feet.
He knows the perimeter is found using the expression 2l + 2w, or 2(1 + w).
P = 2(8 + 4.5)
P = 2(12.5)
P = 25 feet.

Question 9.
A cube has an edge length, s, of 5 centimeters. The expression 6s² gives the surface area of the cube and the expression s³ gives the volume. What are the volume and surface area of the cube?
surface area = cm²
volume = cm³
Answer:
A cube has an edge length, s, of 5 centimeters.
The expression 6s² gives the surface area of the cube
s = 5 cm
surface area = 6(5)² = 6 × 25 = 150 sq. cm
the expression s³ gives the volume.
Volume = 6(5)³ = 6 × 125 = 750 cubic centimeters

Question 10.
Use Structure A right triangle has a base, b, that is 6 inches. The area of the triangle, with h representing the height, is given by the expression \(\frac{bh}{2}\). Complete the table to show how the area of the triangle changes with height:

How does the area change as the height increases? Why do you think this happens?
Answer:
Given,
A right triangle has a base, b, that is 6 inches.
The area of the triangle, with h representing the height, is given by the expression \(\frac{bh}{2}\).
b = 6 in.
h = 4 in
Area = \(\frac{bh}{2}\)
Area = \(\frac{6.4}{2}\) = \(\frac{24}{2}\) = 12 sq. in.
b = 6 in.
h = 5 in
Area = \(\frac{bh}{2}\)
Area = \(\frac{6.5}{2}\) = \(\frac{30}{2}\) = 15 sq. in.
b = 6 in.
h = 6 in
Area = \(\frac{bh}{2}\)
Area = \(\frac{6.6}{2}\) = \(\frac{36}{2}\) = 18 sq. in.
b = 6 in.
h = 7 in
Area = \(\frac{bh}{2}\)
Area = \(\frac{6.7}{2}\) = \(\frac{42}{2}\) = 21 sq. in.
b = 6 in.
h = 8 in
Area = \(\frac{bh}{2}\)
Area = \(\frac{6.8}{2}\) = \(\frac{48}{2}\) = 24 sq. in.

In Problems 11—14, evaluate the expression for n = 0.75.

Question 11.
4n
Answer:
Given,
n = 0.75
4 × 0.75 = 3

Question 12.
6 – n
Answer:
Given,
6 – n
n = 0.75
6 – 0.75 = 5.25

Question 13.
n + 12.5
Answer:
Given,
n + 12.5
n = 0.75
0.75 + 12.5 = 13.25

Question 14.
0.5n
Answer:
Given,
0.5n
n = 0.75
0.5 × 0.75 = 0.375

Question 15.
Critique Reasoning Bill and Tia are trying to evaluate the expression 5×2 when x = 3. They both agree that 3 should be substituted for x. Tia says they should multiply 3 by 5, and then square the result. Bill says they should square 3 and then multiply by 5. Who is correct and why? What is the value of the expression?
Answer:
Given,
Bill and Tia are trying to evaluate the expression 5x² when x = 3. They both agree that 3 should be substituted for x.
Tia says they should multiply 3 by 5, and then square the result.
Bill says they should square 3 and then multiply by 5.
5x² when x = 3
5(3)² = 5(9) = 45
So, Bill is correct

Question 16.
STEM The expression (F – 32)\(\frac{5}{9}\) gives the temperature in degrees Celsius (°C) for a given temperature F in degrees Fahrenheit (°F).
A. Find the temperature in degrees Celsius that is equivalent to 77 °F.
Answer:
Given,
(F – 32)\(\frac{5}{9}\)
F = 77 °F
(77 – 32)\(\frac{5}{9}\)
45\(\frac{5}{9}\) = 5 × 5 = 25°C

B. Water freezes at 32 °F. At what temperature does water freeze in degrees Celsius?
Answer:
Given,
(F – 32)\(\frac{5}{9}\)
F = 32 °F
(32 – 32)\(\frac{5}{9}\)
0\(\frac{5}{9}\) = 0°C

Question 17.
To find approximately how many pounds are equivalent to a given number of kilograms, use the expression 2.2k, where k represents kilograms. How many pounds are equivalent to 6.5 kilograms?
Answer:
Given expression is 2.2k
where k = 6.5 kilograms
2.2k = 2.2(6.5) = 14.3 pounds
Therefore 14.3 pounds are equivalent to 6.5 kilograms.

Question 18.
To find the perimeter of a regular octagon, use the expression 8s, where s represents side length. If the side length of a regular octagon is 1.5 feet, what is its perimeter in feet?

Answer:
Given,
length of a regular octagon is 1.5 feet
The perimeter of the octagon = 8s
P = 8 × 1.5
P = 12 feet
Thus the perimeter of the octagon is 12 feet.

Question 19.
A rectangle is twice as long as it is wide. If the width is w, the length is 2w. The area of the rectangle can be found using the expression 2w². If the rectangle is 10 centimeters wide, what is its area in square centimeters?
Answer:
Given,
A rectangle is twice as long as it is wide. If the width is w, the length is 2w.
The area of the rectangle can be found using the expression 2w².
w = 10 cm
length = 2w = 2 × 10 = 20 cm
Area of the rectangle = 2w² = 2(10)² = 2 × 100 = 200 sq. cm

For Problems 20-25, evaluate the expression for the given value.

Question 20.
6w; w = 0.1
Answer:
Given,
6w
w = 0.1
6 × 0.1 = 0.6
6w = 0.6

Question 21.
x + 5\(\frac{1}{4}\); x = 3\(\frac{1}{2}\)
Answer:
Given,
x + 5\(\frac{1}{4}\)
x = 3\(\frac{1}{2}\)
3\(\frac{1}{2}\) + 5\(\frac{1}{4}\)
Add whole numbers
3 + 5 = 8
Add fractions
\(\frac{1}{2}\) + \(\frac{1}{4}\) = \(\frac{3}{4}\)
8 + \(\frac{3}{4}\) = 8\(\frac{3}{4}\)

Question 22.
1.4y; y = 5
Answer:
Given,
1.4y
y = 5
1.4 × 5 = 7
1.4y = 7

Question 23.
\(\frac{48}{k}\), k = 3
Answer:
Given,
\(\frac{48}{k}\),
k = 3
\(\frac{48}{3}\) = 16
\(\frac{48}{k}\) = 16

Question 24.
z⁵; z = 2
Answer:
Given,
z⁵; z = 2
2⁵ = 2 × 2 × 2 × 2 × 2 = 32
So, z⁵ when z = 2

Question 25.
2.5g²; g = 4
Answer:
Given,
2.5g²; g = 4
2.5(4)² = 2.5 × 16 = 40
So, 2.5g² when g = 4 is 40.

Question 26.
Critique Reasoning To evaluate the expression (r + 6)² for r = 7, Sayid says that r should be squared and 6 should be squared, and then the results should be added. Explain why Sayid is incorrect. Then find the value of the expression when r = 7.
Answer:
Sayid says that r should be squared and 6 should be squared, and then the results should be added.
Sayid is incorrect because the first 7 and 6 should be added and then squared.
(r + 6)² for r = 7
(7 + 6)² = (13)² = 169

Question 27.
Evaluate the expression 4a² – \(\frac{b}{6}\) when a = 6 and b = 36. Show your work.
Answer:
4a² – \(\frac{b}{6}\)
when a = 6 and b = 36
4(6)² – \(\frac{36}{6}\)
4(36) – 6
144 – 6 = 138
4a² – \(\frac{b}{6}\) = 138

Question 28.
Rosa sells pens. She pays $0.75 for each pen and sells them for $1.25 each. She uses the expression 1.25p – 0.75p, where p is the number of pens she sells, to calculate her profit. If Rosa sells 48 pens, what is her profit?

Answer:
Given,
Rosa sells pens. She pays $0.75 for each pen and sells them for $1.25 each.
She uses the expression 1.25p – 0.75p, where p is the number of pens she sells, to calculate her profit.
p = 48
1.25(48) – 0.75(48) = 24
Thus if Rosa sells 48 pens then her profit is $24.

Question 29.
Steve is playing a carnival game. He wants to win a prize, but he thinks he has about a 20% chance of winning. He uses the expression 0.2t to calculate the number of games he can expect to win if he plays t times. If he plays the game 12 times, about how many times can he expect to win?
Answer:
Given,
Steve is playing a carnival game. He wants to win a prize, but he thinks he has about a 20% chance of winning.
He uses the expression 0.2t to calculate the number of games he can expect to win if he plays t times.
0.2(12) = 2.4
2.4 × 20% = 0.48 = 48%

For Problems 30-35, evaluate the expression s³ for the given value.

Question 30.
s = 4
Answer:
Given,
s = 4
To find the expression s³
(4)³ = 4 × 4 × 4 = 64

Question 31.
s = \(\frac{1}{2}\)
Answer:
Given,
s = \(\frac{1}{2}\)
To find the expression s³
(\(\frac{1}{2}\))³ = \(\frac{1}{8}\)

Question 32.
s = 0.3
Answer:
Given,
s = 0.3
To find the expression s³
(0.3)³ = 0.3 × 0.3 × 0.3 = 0.027

Question 33.
s = 10
Answer:
Given,
s = 10
To find the expression s³
(10)³ = 10 × 10 × 10 = 1000

Question 34.
s = 1.2
Answer:
Given,
s = 1.2
To find the expression s³
(1.2)³ = 1.2 × 1.2 × 1.2 = 1.728

Question 35.
s = \(\frac{1}{6}\)
Answer:
Given,
s = \(\frac{1}{6}\)
To find the expression s³
(\(\frac{1}{6}\))³ = \(\frac{1}{216}\)

Lesson 8.4 More Practice/Homework

Question 1.
Every day jin reads for 0.75 hour in the morning and 1.25 hours in the evening. He uses the expression 0.75d + 1 .25d to keep track of the number of hours he has read for any number of days, d. If jin reads for 20 days, how many hours has he read? Show your work.
Answer:
Given,
Every day jin reads for 0.75 hour in the morning and 1.25 hours in the evening.
He uses the expression 0.75d + 1 .25d to keep track of the number of hours he has read for any number of days, d.
0.75d + 1.25d = 2d
d = 20
2 × 20 = 40 hours

Question 2.
There are 16 ounces in 1 pound, so the expression \(\frac{z}{16}\), where z represents the number of ounces, can be used to find the number of pounds for any given number of ounces. How many pounds are in 40 ounces?

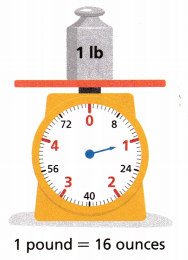
Answer:
Given,
1 pound = 16 ounces
the expression \(\frac{z}{16}\)
z = 40
\(\frac{z}{16}\) = \(\frac{40}{16}\) = 2.5 pounds
Thus there are 2.5 pounds in 40 ounces

Question 3.
Jeffrey is 5 years older than his brother. If j represents Jeffrey’s age, the expression j – 5 can be used to find his brother’s age. If Jeffrey is 23, how old is his brother?
Answer:
Given,
Jeffrey is 5 years older than his brother.
The expression j – 5 can be used to find his brother’s age.
j = 23
23 – 5 = 18
Thus the age of his brother is 18 years.

Math on the Spot For Problems 4-6, evaluate each expression.

Question 4.
4x – 5 for x = 10
Answer:
4x – 5 for x = 10
4(10)-5 = 40 – 5 = 35
4x – 5 = 35

Question 5.
w ÷ 5 + w for w = 20
Answer:
w ÷ 5 + w for w = 20
20 ÷ 5 + 20
4 + 20 = 24
w ÷ 5 + w = 24

Question 6.
3z² – 6z for z = 5
Answer:
3z² – 6z for z = 5
z(3z – 6)
5(3(5) – 6)
5(15 – 6)
5(9) = 45
3z² – 6z = 45

For Problems 7-10, evaluate each expression for b = 5.

Question 7.
2.1b
Answer:
2.1b
b = 5
2.1(5) = 10.5

Question 8.
5b – 12.4
Answer:
5b – 12.4
b = 5
5(5) – 12.4
25 – 12.4 = 12.6

Question 9.
7.4b
Answer:
7.4b
b = 5
7.4(5) = 37
7.4b = 37

Question 10.
4b²
Answer:
4b² = 4(5)²
b = 5
4 × 25 = 100

Test Prep

Question 11.
What is the value of the expression 8w – 4j² when w = 0.25 and j = 0.5?
Answer:
Given,
The value of the expression 8w – 4j² when w = 0.25 and j = 0.5
8w – 4j² = 8(0.25) – 4(0.5)²
= 2 – 4(0.25)
= 2 – 1 = 1
8w – 4j² = 1

Question 12.
What is the first step in evaluating an expression for given variable values?
Answer:
The first step in evaluating an expression for given variable values is to substitute the values 0.25 and 0.5 in the place of w and j.
And then we have to multiply and simplify the expression.

Question 13.
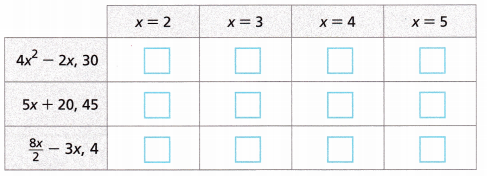
Match the expression and its value to the value of x that gives the expression its value by filling in the box in the correct column.

Answer:

Explanation:
4x² – 2x for x = 2
4x² – 2x = 4(2)² – 2(2)
4(4) – 4 = 16 – 4 = 12
4x² – 2x for x = 3
4x² – 2x = 4(3)² – 2(3)
4(9) – 6 = 36 – 6 = 30
5x + 20 for x = 2
5(2) + 20 = 10 + 20 = 30
5x + 20 for x = 3
5(3) + 20 = 15 + 20 = 35
5x + 20 for x = 4
5(4) + 20 = 20 + 20 = 40
5x + 20 for x = 5
5(5) + 20 = 25 + 20 = 45
8x/2 – 3x for x = 2
8(2)/2 – 3(2)
8 – 6 = 2
8x/2 – 3x for x = 3
8(3)/2 – 3(3)
12 – 9 = 3
8x/2 – 3x for x = 4
8(4)/2 – 3(4)
16 – 12 = 4

Question 14.
Evaluate the expression 4(n + 3) – 5r for n = \(\frac{1}{4}\) and r = \(\frac{1}{5}\).
(A) 3
(B) 5
(C) 8
(D) 12
Answer:
Given,
4(n + 3) – 5r
where
n = \(\frac{1}{4}\) and r = \(\frac{1}{5}\)
4(n + 3) – 5r = 4(\(\frac{1}{4}\) + 3) – 5\(\frac{1}{5}\)
4(n + 3) – 5r = 4(3\(\frac{1}{4}\)) – 1
4(n + 3) – 5r = 4(\(\frac{13}{4}\)) – 1
4(n + 3) – 5r = 13 – 1
4(n + 3) – 5r = 12
Option D is the correct answer.

Question 15.
The surface area for a rectangular prism with a square base is given by the expression 2s² + 4sh, where s is the side length of the square base and h is the height of the prism. What is the surface area in square feet of a rectangular prism when s = 4 feet and h = 6 feet?
Answer:
Given,
The surface area for a rectangular prism with a square base is given by the expression 2s² + 4sh,
Where s is the side length of the square base and
h is the height of the prism.
s = 4 feet and h = 6 feet
A = 2s(s + 2h)
A = 2(4)(4 + 2(6))
A = 8(4 + 12)
A = 8(16)
A = 128 sq. feet

Spiral Review

Question 16.
Write a numerical expression to represent the phrase “the sum of 25 and the cube of 9.” Do not evaluate the expression.
Answer:
the sum of 25 and the cube of 9 is 25 + 9³

Question 17.
A customer at a department store has $45.75. How many neckties can the customer buy if each tie costs $15.25?
Answer:
Given that,
A customer at a department store has $45.75.
To find:
How many neckties can the customer buy if each tie costs $15.25
We have to divide 45.75 by 15.25
45.75/15.25 = 3
Thus the customer can buy 3 neckties.

Question 18.
An expression is shown.
5[8(7 – 4) ÷ 6]
What is the value of the expression?
Answer:
Given,
5[8(7 – 4) ÷ 6]
5[8(3) ÷ 6]
5[24 ÷ 6]
5[4] = 20