We included HMH Into Math Grade 6 Answer Key PDF Module 5 Lesson 1 Understand the Concept and Language of Ratios to make students experts in learning maths.
HMH Into Math Grade 6 Module 5 Lesson 1 Answer Key Understand the Concept and Language of Ratios
write ratios in three different ways given a diagram or a description.
Spark Your Learning
Jace and Keiko each take care of several birdhouses. Jace thinks his birdhouses are more popular but Keiko disagrees. They decide to test their conjectures. They both count the number of birds that visit their birdhouses in one afternoon. Jace counts 12 birds that visit his 5 birdhouses, while 15 birds visit Keiko’s 6 birdhouses. Whose birdhouses are more popular?


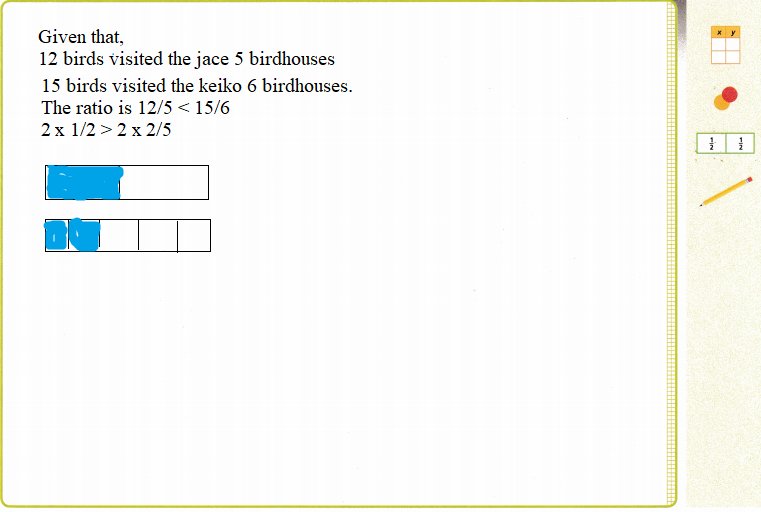
Turn and Talk Share your solutions. Did you use the same method? If not, explain your reasoning to make sure both methods are correct.
Build Understanding
1. Tyree’s cat has a litter of black and orange kittens. The tape diagram shows the number of each color kitten in the litter, with each section representing 1 kitten. What are different ways that Tyree can compare the numbers of kittens?
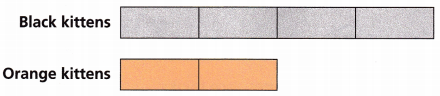
A. How many orange kittens are there? How many black kittens? Write a comparison between the number of orange kittens and the number of black kittens beginning with “For each . . . .”

__________________________
__________________________
Answer:
Given that,
The total number of black kittens = 4
The total number of orange kittens = 2
The comparison between the number of orange kittens and the number of black kittens is.
For each orange kitten, there are 2 black kittens.
B. How does the number of orange kittens compare to the total number of kittens in the litter? Write the comparison beginning with “For every . . . .”
__________________________
__________________________
Answer:
Given that,
The total number of black kittens = 4
The total number of kittens = 4 + 2 = 6
The comparison between the number of orange kittens and the total number of kittens is.
For every 2 orange kittens, there are 6 total numbers of kittens.
C. How does the number of black kittens compare to the total number of kittens in the litter? Write the comparison beginning with “For every .. . .”
__________________________
__________________________
Answer:
Given that,
The total number of black kittens = 4
The total number of kittens = 2 + 4 = 6
The comparison between the number of black kittens and the total number of kittens is.
For every 4 black kittens, there are 6 total numbers of kittens.
D. Suppose each section of the tape diagram represents 2 kittens rather than 1 kitten. Will that change the comparisons in Parts A and B? Why or why not?
Part A: __________________________
__________________________
Part B: __________________________
__________________________
Answer:
Part A
Each section of the tape diagram represents 1 kitten.
The total number of black kittens = 4
The total number of orange kittens = 2
Part B
Each section of the tape diagram represents 2 kittens.
The total number of black kittens = 4 x 2 = 8
The total number of orange kittens = 2 x 2 = 4.
The comparison of part A and Part B will not change. Because 8/4 = 4/2.
Turn and Talk Suppose the model represents a group of orange and black kittens with 16 orange kittens. How many kittens are there in all? Explain.
Answer:
A ratio can be written in several different ways.
5 to 4 5:4 \(\frac{5}{4}\)
Connect to Vocabulary
A ratio is a comparison of two quantities by division, a:b; \(\frac{a}{b}\) or a to b, where b is not equal to 0 (b ≠ 0).
A ratio can compare a part to a part, a part to the whole, or the whole to a part. The quantities in a ratio are sometimes called terms.
2. Aaron is making a quilt for a craft fair. The quilt is made with four different fabric colors as shown in the picture.
A. Complete the tape diagram to model the ratio of the number of blue squares to the number of white squares in the quilt.

![]()
Answer:
The total number of blue squares = 3
The total number of white squares = 5
The ratio of blue squares to the white squares = 3: 5
![]()
B. Complete the statements to describe the ratio of blue squares to white squares in Part A.
For every ___ there are ____.
__________________________
__________________________
Answer:

For every 3 blue squares, there are 5 white squares.
C. Write a part-to-whole or whole-to-part comparison about the quilt using symbols and using ratio language, such as “for each,” “for every,” or “per.”
__________________________
__________________________
Answer:
The total number of blue squares = 3
The total squares = 15.
The ratio is 3: 15.
For every 3 blue squares, there are 15 total squares.
D. For every small green square, there are 2 large green squares. Does this mean that 1 out of every 2 green squares is small? Why or why not?
__________________________
Answer:
The total number of green squares = 3
So, 1 out of every green square is small.
Check Understanding
Question 1.
Describe in ratio language and with symbols the relationship between the number of tails and the number of legs on a dog.
__________________________
Answer:
Number of tails on a dog = 1.
The number of legs on a dog = 4.
The ratio is 1: 4, 1/4, 1 to 4.
Question 2.
A recipe that makes 8 cups of limeade uses 2 cups of lime juice. Describe the related ratio 2:8 using ratio language. Does the ratio involve only parts, or does it involve a part and the whole?
Answer:
Given that,
The total number of limeade cups = 8
The total number of lime juice = 2.
The given ratio is 2: 8
For every 2 cups of lime juice, the recipe makes 8 cups of limeade.
So, the ratio involves a part and a whole.
On Your Own
In Problems 3 and 4, a bag of trail mix contains 3 ounces of peanuts, 6 ounces of cranberries, 2 ounces of almonds, and 2 ounces of raisins. Write each ratio three different ways.
Question 3.
What is the ratio of ounces of peanuts to ounces of almonds?
__________________________
Answer:
Given that,
The ounces of peanuts = 3.
The ounces of almonds = 2.
The ratio of ounces of peanuts to ounces of almonds = 3: 2
The ratio in the three different ways is the colon, the fraction, and the word to.
Therefore the ratios are 3: 2, 3/2, 3 to 2.
Question 4.
What is the ratio of ounces of cranberries to ounces of trail mix?
__________________________
Answer:
Given that,
The ounces of cranberries = 6.
The ounces of trail mix = 3 + 6 + 2 + 2 = 13.
The ratio of ounces of cranberries to ounces of trail mix = 6: 13
The ratio in the three different ways is the colon, the fraction, and the word to.
Therefore the ratios are 6: 13, 6/13, 6 to 13.
In Problems 5 and 6, a carpenter is buying materials. The carpenter needs 36 screws that are 1.5 inches long, 24 screws that are 2 inches long, and 12 screws that are 2.5 inches long. Write each ratio in three different ways.
Question 5.
What is the ratio of 1.5-inch screws to 2.5-inch screws?
Answer:
Given that,
The total number of 1.5-inch screws = 36
The total number of 2.5-inch screws = 12
The ratio of 1.5-inch screws to 2.5-inch screws = 36 : 12
The ratio in the three different ways is the colon, the fraction, and the word to.
Therefore the ratios are 36: 12, 36/12, 36 to 12

Question 6.
What is the ratio of the total length of the 2-inch screws to the total length of all the screws?
Answer:
The total length of the 2 inch screws = 24 x 2 = 48
The total length of all the screws = 36 x 1.5 + 16 x 2.5 + 24 x 2 = 132 inches.
The ratio of the total length of the 2-inch screws to the total length of all the screws = 48: 132
The ratio in the three different ways is the colon, the fraction, and the word to.
Therefore the ratios are 48: 132, 48/132, 48 to 132
Question 7.
Critique Reasoning Alfred mixes 1 part cleanser with 3 parts water to make a cleaning solution. Alfred says that the ratio of cleaning solution to cleanser is 3:1. Is he correct? Why or why not.
Answer:
Given that,
Alfred mixes cleanser = 1 part.
Alfred mixes water = in 3 parts.
The total number of parts = 4
The ratio of cleaning solution to cleanser = 4: 1
Alfred says that the ratio of cleaning solution to cleanser is 3 :1.
So, he is incorrect. Because the Alfred mixes 1 part of cleanser with 3 parts of water
Question 8.
Open Ended Write a statement using ratio language that could describe a part-to-whole ratio of 7:10.
__________________________
__________________________
Answer:
The statement is that there are 7 apples and 10 oranges. Find the ratio of apples and oranges.
I’m in a Learning Mindset!
How does my mindset affect my confidence with depicting ratios using a tape diagram?
__________________________
__________________________
Answer:
The tape diagram is useful to the students for complex problems. It means comparing ratios. The comparing problems are more difficult to solve without the tape diagrams. By using the tape diagram sometimes the answer is readily available.
Lesson 5.1 More Practice/Homework
Question 1.
An aquarium contains 20 African cichlids and 7 botia baches. Compare the number of botia baches to African cichlids beginning with the words “For every. . . .“
__________________________
Answer:
Given that,
The total number of African cichlids in the aquarium is = 20.
The total number of botia baches in the aquarium = 7.
Comparing the number of botia baches to the African cichlids with the words is.
For every 7 botia baches, there are 20 African cichlids
Question 2.
Math on the Spot Carrie collects antique chess pieces. The table gives the number of each type of piece she has in her collection. Use the data to write each ratio in three different ways.
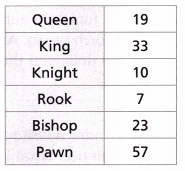
A. Pawn to queens: _____
Answer:
The total number of Pawn pieces = 57
The total number of queen pieces = 19.
The ratio in the three different ways is the colon, the fraction, and the word to.
Therefore the ratios are 57: 19, 57/19, 57 to 19.
B. Rooks to total pieces: _____
Answer:
The total number of queen pieces = 19
The total number of king pieces = 33
The total number of knight pieces = 10
The total number of rook pieces = 7
The total number of bishop pieces = 23
The total number of Pawn pieces = 57
The total pieces = 19 + 33 + 10 + 7 + 23 + 57 = 149
The ratio in the three different ways is the colon, the fraction, and the word to.
Therefore the ratios are 7: 149, 7/149, and 7 to 149.
Question 3.
A ratio of 4 to 1 can represent the number of tires on a car. Use the words for every for each, and per to complete the statements about the ratio 4 to 1.
There are ![]() tires ____ car.
tires ____ car.
There are ![]() tires ____ car.
tires ____ car.
There are ![]() tires ___ car.
tires ___ car.
Answer:
There are 4 tires for each car.
There are 4 tires for every car.
There are 4 tires per car.
Question 4.
A survey asks 25 people if they prefer Brand A or Brand B laundry detergent. The data show that 12 people prefer Brand A. Write a ratio, in three ways, to describe the relationship between the people who prefer Brand B and all the people surveyed.
Answer:
Given that,
The total number of people in the survey was 25.
The total number of people who prefer Brand A = 12.
The total number of people prefer Brand B = 25 – 12 = 13.
The ratio in the three different ways is the colon, the fraction, and the word to.
Therefore the ratio of the people who prefer Brand B and all the people surveyed = 13: 25, 13/25, 13 to 25.
Question 5.
Attend to Precision The amount of food a dog should eat daily is based on its weight. The picture shows the ratio of weight to cups of food. What is the ratio of cups of dog food to the dog’s weight in pounds? If a 100-pound dog is fed 4 cups of food a day, is this the correct ratio? Why or why not?

Answer:
Given that,
The weight of the dog = 50 pounds
The total cups of the food that the dog eats = 2 cups.
The ratio of cups of dog food to the dog’s weight in pounds = 50: 2.
I suppose,
The weight of the dog = 100 pounds
The total cups of the food that the dog eats = 4 cups.
The ratio of cups of dog food to the dog’s weight in pounds = 100: 4.
Yes, it is the correct answer.
Question 6.
Open Ended Write a statement using ratio language that could describe a part-to-part ratio of 4:7.
__________________________
__________________________
Answer:
The statement using the ratio language is Geetha has 4 white balloons and 7 black balloons. Find the ratio of white and black balloons.
Test Prep
Question 7.
Marta has a bracelet made up of 3 red, 5 yellow, and 24 green beads. What is the ratio of yellow beads to beads that are not yellow?
A. 5:3
B. 5:24
C. 5:27
D. 5:32
Answer:
Given that,
The total number of red Beads = 3
The total number of yellow Beads = 5
The total number of Green Breads = 24.
The ratio of yellow beads to beads that are not yellow = yellow beads: red beads + green beads.
= 5 : 24 + 3
= 5 : 27
Option C is the correct answer.
Question 8.
A furniture builder pays $100 for the materials necessary to build one porch swing. A store sells the swing for $250. What is the ratio of the cost in dollars of the materials to the sale price in dollars?
__________________________
Answer:
Given that,
A furniture builder pays $100 for the materials to build one porch swing = $100.
A store sells the swing for $250.
The ratio of the cost of the materials to the sale price = $100 : $250
= $100/$250 = $2/$5
Therefore the ratio of the cost of the materials to the sale price is $2: $5.
Question 9.
Andre is writing a paper for science class. He can type 30 words per minute. What is the ratio of words to minutes?
________________
Answer:
Given that,
Andre types 30 words per minute.
The ratio of words to minutes = 30: 1
Question 10.
A bread recipe uses 2 cups of white flour and 5 cups of whole wheat flour. Which statements are true? Select all that apply.
A. The ratio of white flour to whole wheat flour is 2 to 5.
B. The ratio of whole wheat flour to total flour is 5:7.
C. For every 2 cups of white flour, there are 3 cups of whole wheat flour.
D. For every 7 cups of flour, there are 2 cups of white flour.
E. For each cup of white flour, there are 4 cups of whole wheat flour.
Answer:
The ratio of white flour to whole wheat flour is 2 to 5.
For every 7 cups of flour, there are 2 cups of white flour.
These two statements are true.
Options A and D are correct.
Spiral Review
Question 11.
Viktor purchases a car for $10,608. He makes monthly payments for 48 months in order to pay off the car. He does not pay interest. How much are his payments each month?
__________________________
Answer:
Given that,
The total cost of the car = $10,608.
The total number of months that Viktor pays = 48 months.
For each month Viktor payment = $10,608/48 = $221.
Therefore Viktor’s payment for each month = $221.
Question 12.
A professional running track has two straight sections that are each 328.084 feet long. The total distance around the track is 1,312.34 feet. What is the length of the part of the track that is not straight?
__________________________
Answer:
Given that,
The length is of the two straight sections each = 328.084 feet long.
The total distance around the track is 1,312.34 feet.
The formula for the length of the track that is not straight = total distance – 2 x (straight sections).
Section not straight = 1,312.34 – 2 x 328.084
Section not straight = 1,312.34 – 656.168
Section not straight = 656.172 feets.
Question 13.
What is the greatest common factor of 72 and 34?
__________________________
Answer:
The prime factorization of 34 is 2 x 17.
The prime factorization of 72 is 2 x 2 x 2 x 3 x 3.
The greatest common factor of 72 and 34 is 2.