Into Math Grade 6 Module 7 Lesson 3 Answer Key Solve a Variety of Percent Problems

We included HMH Into Math Grade 6 Answer Key PDF Module 7 Lesson 3 Solve a Variety of Percent Problems to make students experts in learning maths.

HMH Into Math Grade 6 Module 7 Lesson 3 Answer Key Solve a Variety of Percent Problems

I Can write a percent as a fraction or a decimal and use a variety of strategies to solve real-world problems.

Step It Out

1. Liz is collecting aluminum cans for a school fundraiser. So far, she has collected 16 cans, which is 20% of her goal. How many cans must she collect to reach her goal?

A. Use a double number line to solve the problem. When Liz reaches 100%, she has reached her goal. Complete the double number line until you reach 100%.

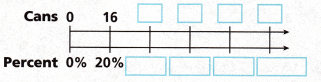
B. For every 16 cans Liz collects, she adds % toward her goal. If she reaches 40% of her goal she will have cans. Liz must collect cans to reach her goal.
A.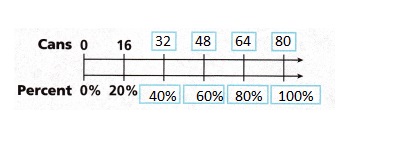
B. For every 16 cans Liz collects, she adds 20% toward her goal,
If she reaches 40% of her goal she will have 32 cans.
Liz must collect 80 cans to reach her goal,

Explanation:
Given Liz is collecting aluminum cans for a school fundraiser.
So far, she has collected 16 cans, which is 20% of her goal.
A.Used a double number line to solve the problem.
When Liz reaches 100%, she has reached her goal.
Completed the double number line until I reached 100%
as shown above.
B. For every 16 cans Liz collects, she adds 20% toward her goal,
If she reaches 40% of her goal she will have more 16 cans,
16 + 16 = 32 cans. To reach her goal she needs 5 times more
than 20% so it is 16 X 5 = 80 cans, therefore
For every 16 cans Liz collects, she adds 20% toward her goal,
If she reaches 40% of her goal she will have 32 cans.
Liz must collect 80 cans to reach her goal.

2. Jose is in the same class as Liz and he is also collecting aluminum cans. He has collected 36 cans, which is 18% of his goal. How many cans must Jose collect to reach his goal?
A. Use equivalent ratios to solve the problem. One ratio is the percent:
The second ratio is the number of cans already collected compared to the total number of cans that must be collected. You know the first number, the part, of the ratio. You must find the second number, the whole, of the ratio. Complete the ratio. The gray box represents the unknown number.
B. Find equivalent ratios: Eighteen is multiplied by to get . Multiply 100 by the same amount to find the answer. 100 × = . Jose must collect cans to reach his goal.
Answer:
A. One ratio percent is \(\frac{18}{100}\),
The unknown number is \(\frac{36}{x}\),
B. Equivalent ratios are \(\frac{18}{100}\) = \(\frac{36}{x}\) ,
Eighteen is multiplied by x to get 18x.
Multiply 100 by the same amount  100 × 36 = 3,600.
Jose must collect 200 cans to reach his goal.

Explanation:
Given Jose is in the same class as Liz and he is also collecting
aluminum cans. He has collected 36 cans, which is 18% of his goal.
A. Used equivalent ratios to solve the problem.
One ratio is the percent: \(\frac{18}{100}\),
The second ratio is the number of cans already collected
compared to the total number of cans that must be collected.
The first number, the part, of the ratio.
To find the second number the whole of the ratio is x.
Completed the ratio. The gray box represents the unknown number.
as \(\frac{36}{x}\),
B. Finding equivalent ratios: \(\frac{18}{100}\) = \(\frac{36}{x}\),
Eighteen is multiplied by x to get 18x.
Multiply 100 by the same amount to 36 we get
100 × 36 = 3,600. so x = \(\frac{3600}{18}\) = 200,
Therefore Jose must collect 200 cans to reach his goal.

Turn and Talk Which method do you think is easier to use: a double number line or finding equivalent ratios? Explain.
Answer:
Both gives result easier is equivalent ratios but
model wise and understanding double number line is good,

Explanation:
Both methods gives result I thing easier is equivalent ratios,
but to understand and model wise representation
double number line is ok.

3. In Big Bog in Maui, Hawaii, about 400 inches of rain falls during a normal year. It is the 7^th wettest place in the world, judging by annual rainfall. If 364 inches of rain have fallen so far and you expect the rainfall to reach the usual yearly amount, what percent of the year’s rain has already fallen? Use equivalent ratios to find the solution.

A. You know one ratio already, the rainfall so far and the total rainfall expected. Write the ratio in fraction form.
B. What ratio do we need to solve for? _____
C. Find equivalent ratios.
D. 400 is divided by to get 100. Divide 364 by the same number to find the percent. 364 ÷ =
E. % of the annual rain has fallen so far.
Answer:
A.\(\frac{364}{400}\) ,
B. 100%,
C. \(\frac{364}{400}\) = \(\frac{x}{100}\) ,
D. 400 is divided by 4 to get 100.
\(\frac{364}{4}\) = 91,
E. 91% of the annual rain has fallen so far,

Explanation:
A. The rainfall so far and the total rainfall expected.
The ratio in fraction form is \(\frac{364}{400}\),
B. We need to solve the ratio for 100%,
C. Equivalent ratios, let x be missing number so
\(\frac{364}{400}\) = \(\frac{x}{100}\),
D. 400 is divided by 4 to get 100.
Dividing 364 by the same number to find the percent.
\(\frac{364}{4}\) = 91,
E. 91% of the annual rain has fallen so far.

Turn and Talk How did you know which ratio to find?
Answer:
Dividing ,

Explanation:
Ratios compare two numbers, usually by dividing them.
If you are comparing one data point (A) to another data point (B),
My formula would be A/B. This means we are dividing
information A by information B. For example, if A is five and
B is 10, my ratio will be 5/10.

Check Understanding

Question 1.
In a city election, 5,000 people voted for mayor. If the new mayor received 60% of the votes, how many people voted for the new mayor? Show how you know.
Answer:
3000 people voted for the new mayor,

Explanation:
Given  in a city election, 5,000 people voted for mayor.
If the new mayor received 60% of the votes, Number of
people voted for the new mayor are
5000 X \(\frac{60}{100}\) = 3,000 people.

Question 2.
At the King School, 55% of the students take a bus to school. If 220 students take a bus to school, how many students are there in total?
___________
Answer:
400 students,

Explanation:
Given at the King School, 55% of the students take a bus to school.
If 220 students take a bus to school, let x be students are there in total
so x X \(\frac{55}{100}\) = 220,
x = 220 X \(\frac{100}{55}\) = 400 students.

Question 3.
When Randy is 3 years old, the doctor tells his parents that Randy will be 180 centimeters tall when he is fully grown. If Randy is 90 centimeters tall now, what percent of his expected adult height is he?
Answer:
50%,

Explanation:
Given when Randy is 3 years old, the doctor tells his
parents that Randy will be 180 centimeters tall
when he is fully grown. If Randy is 90 centimeters tall now means
let x is his expected percent of adult height he is so
x = 100 X \(\frac{90}{180}\) = 50%.

Question 4.
On a math test, Janice answers 85% of the questions correctly. If she answered 17 questions correctly, how many questions are on the test?
Answer:
20 questions,

Explanation:
Given on a math test, Janice answers 85% of the
questions correctly. If she answered 17 questions correctly,
Let x be number of questions are on the test so
x = 100 X \(\frac{17}{85}\) = 20 questions.

On Your Own

Question 5.
There are 8 equally sized slices in a pizza. If Ken eats 5 of the slices, what percent of the pizza has he eaten? Show your work.
Answer:
62.5%,

Explanation:
Given there are 8 equally sized slices in a pizza.
If Ken eats 5 of the slices, Let x be percent of the pizza
has he eaten so x = 100 X \(\frac{5}{8}\) = 62.5%.

Question 6.
An animal shelter offers kittens and puppies each day for adoption. The shelter director wants 40% of the animals offered to be kittens. Fill in the double number line diagram to find out how many kittens should be included if the shelter offers 20 animals for adoption.

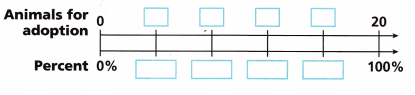
Answer:

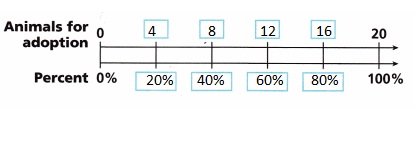
Explanation:
Given an animal shelter offers kittens and puppies
each day for adoption. The shelter director wants 40% of
the animals offered to be kittens. Filled in the double number
line diagram to finding out how many kittens should be
included if the shelter offers 20 animals for adoption for
20% animal adoption is 20 X \(\frac{20}{100}\) = 4,
40% animal adoption is 20 X \(\frac{40}{100}\) = 8,
60% animal adoption is 20 X \(\frac{60}{100}\) = 12,
80% animal adoption is 20 X \(\frac{80}{100}\) = 16,
100% animal adoption is 20 X \(\frac{100}{100}\) = 20
as shown above.

Question 7.
A zoo has the ratio of giraffes to zebras shown. What percent of this grouping of animals are giraffes? What percent of this grouping are zebras?

Answer:
25% of this grouping are zebras,

Explanation:
Given a zoo has the ratio of giraffes to zebras shown.
The percent of this grouping of animals are giraffes are
100 X \(\frac{1}{4}\) = 25% of this grouping are zebras.

Question 8.
About \(\frac{39}{50}\) of Earth’s atmosphere is made up of nitrogen. Use equivalent ratios to find about what percent of the atmosphere is nitrogen.
Answer:
78%,

Explanation:
Given about \(\frac{39}{50}\) of Earth’s atmosphere is
made up of nitrogen. Using equivalent ratios to finding about
what percent of the atmosphere is nitrogen
\(\frac{39}{50}\) X 100 = 78%.

Question 9.
Critique Reasoning Andy has read 126 pages of a biography that has 300 pages. He says that he has read 60% of the book. Is this percent reasonable? Why or why not?
______________________
______________________
Answer:
Not reasonable, it is 180 pages not 126 pages,

Explanation:
Given Andy has read 126 pages of a biography that has
300 pages. He says that he has read 60% of the book.
This percent is not reasonable as 60% of 300 pages is
300 X \(\frac{60}{100}\) = 180 pages but
Andy read 126 pages which is not 60%.

Question 10.
STEM The average adult is about 60% water. One liter of water has a mass of 1 kilogram. If a person’s body contains 45 liters of water, what is the person’s mass in kilograms? ______
Answer:
75 kg,

Explanation:
Given the average adult is about 60% water.
One liter of water has a mass of 1 kilogram.
If a person’s body contains 45 liters of water,
Let x be the person’s mass in kilograms so
x X \(\frac{60}{100}\) = 45,
x = 45 X \(\frac{100}{60}\) = 75 kg.

For Problems 11—16 find the unknown value.

Question 11.
25% of 48 =
Answer:
12,

Explanation:
25% of 48 is
\(\frac{25}{100}\) X 48 = 12.

Question 12.
75 % of 60 =
Answer:
45,

Explanation:
75% of 60 is
\(\frac{75}{100}\) X 60 = 45.

Question 13.
40% of 72 =
Answer:
28.8%,

Explanation:
40% of 72 is
\(\frac{40}{100}\) X 72 = 28.8%.

Question 14.
100% of = 30
Answer:
30,

Explanation:
Let x be missing number of
100% of x = 30,
\(\frac{100}{100}\) X x = 30,
x = 30 X \(\frac{100}{100}\),
x = 30.

Question 15.
30% of = 30
Answer:
100,

Explanation:
Let x be missing number of
30% of x = 30,
\(\frac{30}{100}\) X x = 30,
x = 30 X \(\frac{100}{30}\),
x = 100.

Question 16.
120% of = 18
Answer:
15,

Explanation:
Let x be missing number of
120% of x = 18,
\(\frac{120}{100}\) X x = 18,
x = 18 X \(\frac{100}{120}\),
x = 15.

Question 17.
Reason Lily is using the equivalent ratios to find the unknown whole value. What factor should she multiply 100 by? Explain how you found the factor.
Answer:
1100,

Explanation:
Given Lily is using the equivalent ratios to find the
unknown whole value. The factor should she multiply 100 by
is let it be x so \(\frac{7}{100}\) = \(\frac{77}{x}\),
x = 77 X \(\frac{100}{7}\) = 11 X 100 = 1,100.

Question 18.
If the gas tank in Glen’s car can hold 12 gallons and it is 80% full, how many gallons of gas are in the gas tank?
Answer:
9.6 gallons,

Explanation:
Given if the gas tank in Glen’s car can hold 12 gallons and
it is 80% full, Number of many gallons of gas are in the gas tank
are 12 X \(\frac{80}{100}\) = 9.6 gallons.

Question 19.
A water tank in the shape of a cylinder contains 54,000 gallons of water. If the tank is only 60% filled, how many gallons of water can the tank hold?

Answer:
90,000 gallons of water the tank can hold,

Explanation:
Given a water tank in the shape of a cylinder contains
54,000 gallons of water. If the tank is only 60% filled,
Let x be number of gallons of water can the tank hold is
x X \(\frac{60}{100}\) = 54,000,
x = 54,000 X \(\frac{100}{60}\) = 90,000 gallons.

Question 20.
Melinda earned $550 in one month and saved 30% of her earnings. She is saving for a new bicycle which costs $825. How much has Melinda saved so far? At this rate, how long will it take her to save enough money to buy the bicycle?
Answer:
Melinda saved $165, 5 months,

Explanation:
Given Melinda earned $550 in one month and saved 30% of
her earnings. She is saving for a new bicycle which costs $825.
So much has Melinda saved so far is $550 X \(\frac{30}{100}\) =
$165 and long will it take her to save enough money
to buy the bicycle \(\frac{825}{165}\) = 5 months.

Question 21.
In a survey of 560 students, 35% chose math as their favorite subject. Use multiplication to find the number of students who chose math.
A. Write the percent in fraction form. 35% =
Answer:
35% = \(\frac{35}{100}\),

Explanation:
Given in a survey of 560 students, 35% choose math as
their favorite subject. Used multiplication to
find the number of students who choose math.
The percent in fraction form is 35% = \(\frac{35}{100}\).

B. How many students chose math? Show your work.
Answer:
196 students choose math,

Explanation:
Number of students who choose math let it be x so
x = \(\frac{35}{100}\) X 560,
x = 196 students.

C. Double-check your answer by converting the percent to a decimal and using decimal multiplication. Write the percent in decimal form. 35% _______
Answer:
0.35,

Explanation:
Double-checking my answer by converting the
percent to a decimal and using decimal multiplication.
The percent in decimal form. 35% is \(\frac{35}{100}\) = 0.35.

D. Multiply the decimal by the total number of students surveyed.
_________________________
Answer:
196 students,

Explanation:
Multiplying the decimal by the total number of students surveyed is
0.35 X 560 = 196 students.

E. Open Ended Which method do you prefer, converting the percent to a fraction and multiplying or converting the percent to a decimal and multiplying? Why?
Answer:
Both methods give results,
I prefer the percent to a fraction and multiplying

Explanation:
Both the methods converting the percent to a fraction and
multiplying or converting the percent to a decimal and
multiplying gives exact results but I would like to prefer
the percent to a fraction and multiplying because in fractions
and multiplying we can easily remove common factors while
multiplication also and calculate.

Lesson 7.3 More Practice/Homework

Solve a Variety of Percent Problems

Question 1.
Nancy hopes to collect 100 oysters from the ocean. She has collected 15% of her goal so far. How many oysters does she have?
___________________

Answer:
15 oysters,

Explanation:
Given Nancy hopes to collect 100 oysters from the ocean.
She has collected 15% of her goal so far.
Number of oysters does she have are 15% of 100 is
\(\frac{15}{100}\) X 100 = 15 oysters.

Question 2.
Math on the Spot Hal is downloading a file from the internet. So far he has downloaded 25% of the file. If 10 minutes have passed since he started, how long will it take to download the rest of the file?
___________________
Answer:
40 minutes,

Explanation:
Given Math on the Spot Hal is downloading a file
from the internet. So far he has downloaded 25% of the file.
If 10 minutes have passed since he started,
Long will it take to download the rest of the file
let it be x minutes so x X \(\frac{25}{100}\) = 10,
x = 10 X \(\frac{100}{25}\) = 40 minutes.

Question 3.
Sally eats lunch at a restaurant and her bill is $12. She would like to leave a 15% tip for the waiter. How much money should she leave?
___________________
Answer:
$1.8,

Explanation:
Given Sally eats lunch at a restaurant and her bill is $12.
She would like to leave a 15% tip for the waiter.
So much money should she leave is let it be x
so x = \(\frac{15}{100}\) X $12 = $1.8.

Question 4.
A town spends 43% of its annual budget on education. If the town’s budget is one million dollars, how much will be spent on education?
___________________
Answer:
$430,000 on education,

Explanation:
Given a town spends 43% of its annual budget on education.
If the town’s budget is one million dollars,
Much will be spent on education if it x amount is
x = \(\frac{43}{100}\) X 1,000,000 = $430,000.

Question 5.
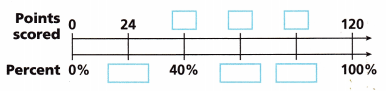
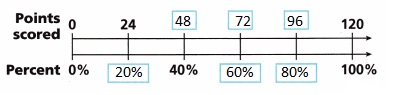
Matt hopes to score 120 points Points this season. He has scored 80% scored of his goal so far. Fill in the double number line diagram to find out how many points he has scored so far and write the answer.

Answer:

Explanation:
Given Matt hopes to score 120 points Points this season.
He has scored 80% scored of his goal so far.
Filled in the double number line diagram to
find out how many points he has scored so far as
20% points scored is 120 X \(\frac{20}{100}\) = 24,
40% points scored is 120 X \(\frac{40}{100}\) = 48,
60% points scored is 120 X \(\frac{60}{100}\) = 72,
80% points scored is 120 X \(\frac{80}{100}\) = 96,
100% points scored is 120 X \(\frac{100}{100}\) = 120
So Matt has scored 96 points.

Question 6.
Attend to Precision On a test Jenna gets 85% of the questions correct, Linda gets 32 out of 40 questions correct, Karl gets \(\frac{7}{8}\) correct, and Julie gets 0.83 of the questions correct. List the students in order
from lowest to highest score.
Answer:
Linda,Julie,Jenna and Karl,

Explanation:
Given on test Jenna gets 85% of the questions correct,
Linda gets 32 out of 40 questions correct,
Karl gets \(\frac{7}{8}\) correct and
Julie gets 0.83 of the questions correct.
Jenna is \(\frac{85}{100}\)= 0.85,
Linda is \(\frac{32}{40}\)= 0.8,
Karl \(\frac{7}{8}\) = =0.875,
As 0.8 < 0.83 < 0.85 < 0.875 so list of the students in order
from lowest to highest score are Linda,Julie,Jenna and Karl.

Question 7.
Students are auditioning for a school play. Only 18 of the 45 students auditioning will get a part in the play. What percent of the students who audition will be in the play? ____
Answer:
40% of students,

Explanation:
Given students are auditioning for a school play.
Only 18 of the 45 students auditioning will get a part in the play.
The percent of the students who audition will be in the play are
\(\frac{18}{45}\) X 100 = 40%.

Question 8.
The first lap of an auto race is 2,500 meters. This is 10% of the total race distance. What is the total race distance? _________
Answer:
25,000 meters,

Explanation:
Given the first lap of an auto race is 2,500 meters.
This is 10% of the total race distance.
The total race distance is let it be x
so x = 2,500 X \(\frac{100}{10}\) = 25,000 meters.

For Problems 9—12, find the unknown value.

Question 9.
200% of 500 is .
Answer:
1,000,

Explanation:
200% of 500 is
\(\frac{200}{100}\) X 500 = 1,000.

Question 10.
35% of 500 is .
Answer:
175,

Explanation:
35% of 500 is
\(\frac{35}{100}\) X 500 = 175.

Question 11.
% of 500 is 100.
Answer:
20%,

Explanation:
Let x be missing number   of
x% of 500 = 100,
\(\frac{x}{100}\) X 500 = 100,
x = 100 X \(\frac{100}{500}\),
x = 20%.

Question 12.
5% of is 25.
Answer:

Explanation:
Let x be missing number of
5% of x = 25,
\(\frac{5}{100}\) X x = 25,
x = 25 X \(\frac{100}{5}\),
x = 500.

Test Prep

Question 13.
In a jar, 25% of the marbles are red. If there are 45 red marbles in the jar, how many marbles are in the jar altogether?
A. 60
B. 70
C. 180
D. 1,125
Answer:
C.180,

Explanation:
Given in a jar, 25% of the marbles are red.
If there are 45 red marbles in the jar,
Number of marbles are in the jar altogether if it x are
\(\frac{25}{100}\) X x = 45,
x = 45 X \(\frac{100}{25}\) = 180
which matches with bit C.

Question 14.
On a 747 airplane, 20% of the seats are business class. If 80 passengers can ride in business class, how many passengers can the plane carry?
A. 100
B. 160
C. 320
D. 400
Answer:
D. 400,

Explanation:
Given on a 747 airplane, 20% of the seats are business class.
If 80 passengers can ride in business class,
Let x be number of passengers can the plane carry are
\(\frac{20}{100}\) X x = 80,
x = 80 X \(\frac{100}{20}\) X x = 400
matches with bit D.

Question 15.
About 10% of people are left-handed. If there are 480 people in a movie theater, about how many of them are likely to be left-handed?
Answer:
48 people,

Explanation:
Given about 10% of people are left-handed.
If there are 480 people in a movie theater
Number of them are likely to be left-handed are
10 X \(\frac{480}{100}\) = 48 people.

Question 16.
Mr. Ramos pays 22% of his income for housing. If Mr. Ramos pays $8,800 for housing, how much money did he earn during the year?
___________________
Answer:
Mr.Ramos earned $40,000 during the year,

Explanation:
Given Mr.Ramos pays 22% of his income for housing.
If Mr. Ramos pays $8,800 for housing,
let x be the money did he earn during the year so
\(\frac{22}{100}\) X x = $8,800,
x = $8,800 X \(\frac{100}{22}\) =
x = $40,000.

Spiral Review

Question 17.
Write 3 ratios that are equivalent to 3 cats for 4 dogs.
___________________
___________________
___________________
Answer:
1. 30 : 40,
2. 75 :100,
3. 9 : 12,

Explanation:
Asked to write 3 ratios that are
equivalent to 3 cats for 4 dogs means
if 3 cats are there then there will be 4 dogs
so the ratio is 3 : 4, Therefore equivalent ratios are
1. 30 : 40 both goes in 10, we get 3 : 4,
2. 75 : 100 both goes in 25, we get 3 : 4,
3. 9 : 12 both goes in 3, we get 3 : 4.

Question 18.
In a circle graph displaying the most popular juice sold to students in the school cafeteria, the ratio of apple juice boxes to total juice boxes sold is \(\frac{3}{4}\). What is the angle measure of the apple juice section of the graph?
Answer:
Angle 270⁰,

Explanation:
Given a circle graph displaying the most popular juice sold to
students in the school cafeteria, the ratio of apple juice boxes to
total juice boxes sold is \(\frac{3}{4}\).
The angle measure of the apple juice section of the graph is as
a circle has complete 360⁰, so it is
\(\frac{3}{4}\) X 360⁰ = 270⁰.

Question 19.
Rose is 60 inches tall. How many feet tall is Rose?
______________________
Answer:
Rose is 4.998 feet approximately 5 feet tall,

Explanation:
Given Rose is 60 inches tall.
Number of many feet tall is Rose as
1 inch is equal to 0.0833 so 60 X 0,0833 =
4.998 approximately 5 feet tall.

Question 20.
Find the values and complete the statement.
A. |—18| = |4| = |97| =
B. In Part A, I found the _____ of each integer.
Answer:
A. 18, 4, 97
B. Absolute value,

Explanation:
Found the values and completed the statement as
A. |—18| = 18, |4| = 4, |97| = 97,
The absolute value of a number is the number’s
distance from zero, which will always be a positive value.
We find the absolute value of a number,
dropping the negative sign if there is one to
make the number positive.
B. In Part A, I found the absolute value of each integer.