Into Math Grade 6 Module 13 Review Answer Key

We included HMH Into Math Grade 6 Answer Key PDF Module 13 Review to make students experts in learning maths.

HMH Into Math Grade 6 Module 13 Review Answer Key

Vocabulary

Choose the correct term from the vocabulary box.

Vocabulary
net
pyramid
surface area

Question 1.
The total area of the faces of a three-dimensional object is the ___________.
Answer:
Surface area.

Explanation:
The total area of the faces of a three-dimensional object is the surface area.

Question 2.
A ___________ is a pattern that you can cut and fold to make a model of a solid shape.
Answer:
Net

Explanation:
A net is a pattern that you can cut and fold to make a model of a solid shape.

Question 3.
A ______________ is a solid with a polygon base and triangular faces that meet at the top.
Answer:
pyramid

Explanation:
A pyramid is solid with a polygon base and triangular faces that meet at the top.

Concepts and Skills

Question 4.
The net shown can be used to form a cube. What is the surface area of the cube formed by the net?

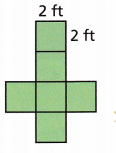
Answer:
The surface area of the cube is 24 ft²

Explanation:
The surface area of the cube = 6 a²
a = 2 ft
Now calculate the area of the cube = 6 × 2 × 2
Area = 24 ft²

Question 5.
A cube has a surface area of 54 square centimeters. What is the volume of the cube?
Answer:
volume of the cube is 27 cm³

Explanation:
Given
Surface area of a cube is 54 square centimeters.
Area = 6 a²
54 = 6 a²
a² = \(\frac{54}{6}\)
a² = √ 9
a = 3 cm
Now calculate the volume of the cube is V=a³
V = 3 × 3 × 3
V = 27 cm³

Question 6.
A painting set is shipped in the box shown. The surface area is printed with advertisements. What is the total area covered by advertisements?
Answer:
528 cm²

Explanation:
The total area covered by advertisements is 528 cm²

Question 7.
Use Tools A rectangular prism is 8 cm long, 11 cm wide, and 5.8 cm tall. What is the volume of the prism? State what strategy and tool you will use to answer the question, explain your choice, and then find the answer.

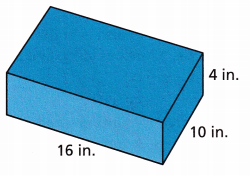
Answer:
Volume = 640 in²

Explanation:
Given,
l = 16 in, width = 10 in and height = 4 in
Volume of the prism is l × w × h
Volume = 16 × 10 × 4
Volume = 640 in²

Question 8.
A box company makes cardboard boxes using flat templates like the one shown. Both squares are congruent, and the remaining four rectangular faces are congruent. What is the surface area of the cardboard box?

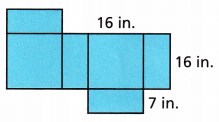
Answer:
The surface area of the cardboard box is 960 in²

Explanation:
The surface area is A=2(wl+hl+hw)
Area = 2 ((16 × 16) + (16 × 7) + (16 × 7))
Area = 2 ((256) + (112) + (112))
Area = 2 (480)
Surface area is 960 in²

Question 9.
What is the volume of the rectangular prism formed by the net?

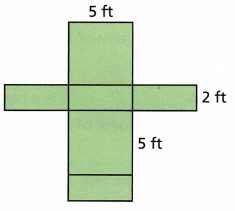
(A) 10 ft³
(B) 50 ft³
(C) 60 ft³
(D) 90 ft³
Answer:
The volume of the rectangular prism formed by the net is 50 ft³

Explanation:
Given,
l = 5 ft, w = 5ft and height = 2 ft
Volume of the prism is l × b × h
Volume = 5 × 5 × 2
Volume = 50 ft³

Question 10.
What are the surface area and volume of the prism?

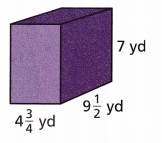
The surface area is ___________.
The volume is ___________.
Answer:
Volume is 315.87 yd³
Surface area is 269.74 yd²

Explanation:
Volume of the prism is l × w × h
l = 4\(\frac{3}{4}\) = \(\frac{19}{4}\) = 4.75
w = 9\(\frac{1}{2}\) = \(\frac{19}{2}\) = 8.5
h = 7 yd
Volume of the prism = \(\frac{19}{4}\) × \(\frac{19}{2}\) × 7
Volume = 315.87 yd³ .
The surface area is A=2(wl+hl+hw)
surface area = 2 ( (8.5 × 4.75) + (7×4.75) + (7×8.5))
Surface area = 2 ((40.37) +(33.25)+ (61.25))
Surface area = 2(134.87)
Surface area = 269.74 yd²

Question 11.
A casserole dish is in the shape of a rectangular prism. The dish is 6 inches wide, 12 inches long, and 5 inches deep. What is the volume of the dish?
Answer:
The volume of the dish is 360 inc³.

Explanation:
The volume of the rectangular prism = l × b × h
Volume = 6 × 12 × 5
Volume = 360 inc³

Question 12.
Jerome is painting a rectangular toolbox that is 20 inches by 10 inches by 8 inches. A tube of paint covers 300 square inches.
A. What is the surface area of the toolbox?
Answer:
The surface area of the toolbox is 880 inches²

Explanation:
The surface area of the rectangle = 2*L*H+2*L*W+2*W*H
Given L = 20, H = 10 inches and W = 8 inches
Surface area = (2 × 20 × 10) + (2 × 20 × 8) + (2 × 8 × 10)
Total surface area = (400) + (320) + (160)
Surface area = 880 inches²

B. How many tubes of paint should Jerome buy?
Answer:
He should buy 3 tubes of paint.

Explanation:
We know that a tube of paint covers 300 of the 880 surface area.
To find the exact amount, lets divide the 880 by the 300
\(\frac{880}{300}\)
\(\frac{44}{15}\)
2.933
Approx 3.
Hence Jerome bought 3 tubes of paint.

Question 13.
A planter in the shape of a rectangular prism is 24 inches by 4 inches by 5 inches. How much dirt is needed to fill the planter?
Answer:
480 in³

Explanation:
The rectangular prism measures 24 inches by 4 inches by 5 inches.
The volume of the planter is length × width × height
Volume = 24 × 4 × 5
Volume = 480 in³