Into Math Grade 6 Module 13 Answer Key Surface Area and Volume

We included HMH Into Math Grade 6 Answer Key PDF Module 13 Surface Area and Volume to make students experts in learning maths.

HMH Into Math Grade 6 Module 13 Answer Key Surface Area and Volume

Pass the Popcorn

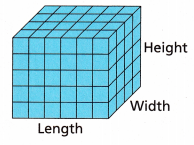
A company that makes microwave popcorn is redesigning its boxes. The diagram shows the company’s current box size, with each face marked off in squares with a side length of 1 inch.

Use the diagram to answer the questions.
A. What is the volume of the company’s current popcorn box?
_________ cubic inches

Answer:
The above-given diagram is like a rectangular prism.
so we have to find out the volume of the rectangular prism that is the company’s current popcorn box.
The Volume of a Rectangular Prism Formula is,
The volume of a rectangular prism = length x width x height
Given that each face side length is 1 inch.
Count the squares.
length = 6; width =4; height = 5
Now calculate the volume.
volume = 6 x 4 x 5
volume = 120 cubic inches.

Turn and Talk

Question 1.
Explain how you determined the volume of the company’s current popcorn box.
Answer:
– First, we have to identify the given box. The popcorn box is identified as a rectangular prism.
– Next, we have to learn the formula for the volume of the rectangular prism.
– We have to find the length, width, and height.
– Substituting the values in the formula v = lwh
– Be sure to express your answer in cubic units.
– rectangle was measured in inches, the volume should be written as 31 cubic inches
Question 2.
Explain how you determined a possible length and height for the new box design.
Answer:
I think the height and length will be the same.
– Firstly, we reduce the width part which means we remove one line.
– So that the area will decrease but not length and height will decrease.

Are You Ready?

Complete these problems to review prior concepts and skills you will need for this module.

Explore Volume

Find the volume of each prism by counting cubic units.

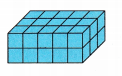
Question 1.

V = _____________
Answer:
The length is 5
The height is 2
The width is 3
The Volume of a Rectangular Prism Formula is,
The volume of a rectangular prism = length x width x height
volume = 5 x 2 x 3
Volume = 30 cubic units.

Question 2.

V = _____________
Answer:
The volume of a prism is defined as the amount of space a prism occupies.
As we know, the volume of the prism is V = B × H.
Given that: B = 3 square inches, H = 2 inches
Thus, the Volume of the prism, V = B × H ⇒ V = 3 × 2 = 6 in³
Therefore, the volume of the prism is 6 cubic inches.

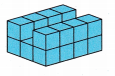
Question 3.

V = _____________
Answer:
The length is 4
The height is 2
The width is 3
The Volume of a Rectangular Prism Formula is,
The volume of a rectangular prism = length x width x height
volume = 4 x 2 x 3
Volume = 24 cubic units.

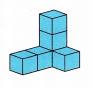
Question 4.

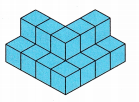
V = _____________
Answer:
Volume of a square = S^3
For the down square S = 4
Volume = 4 x 4 x 4
volume = 64 cubic units
Volume of upward square S = 3
Volume =3 x 3 x 3
volume = 27 cubic units.

Area of Quadrilaterals and Triangles

Find the area of each figure.

Question 5.

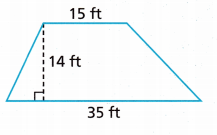
A = ___________
Answer:
area of trapezium:
A trapezium is a quadrilateral, which is defined as a shape with four sides and one set of parallel sides. Thus, the area of the trapezium is the region covered within these four sides. The area of the trapezium basically depends upon the length of parallel sides and the height of the trapezium. It is measured in square units. Let us see the formula to find the area of any trapezium.
Formula:
Trapezium area can be calculated by using the below formula:
Area = (1/2) h (a+b) where,
– a and b are the length of parallel sides/bases of the trapezium
– h is the height or distance between parallel sides.
The given units: a = 35ft; b = 15ft; h = 14ft.
Now substitute the values in the above formula:
Area = 1/2 x 14(35 + 15)
Area = 7(50)
Area = 350 sq.ft

Question 6.

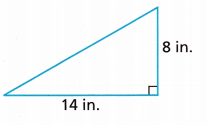
A = ____________
Answer:
the right triangle legs are perpendicular to each other, one leg is taken as a base and the other is a right triangle height:
area = a * b/2
area = 8 x 14/2
area = 112/2
area = 56 square inches.

Question 7.

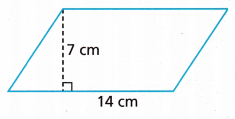
A = ____________
Answer:
The area of a parallelogram is the region bounded by the parallelogram in a given two-dimension space. To recall, a parallelogram is a special type of quadrilateral which has four sides and the pair of opposite sides are parallel. In a parallelogram, the opposite sides are of equal length and opposite angles are of equal measures. Since the rectangle and the parallelogram have similar properties, the area of the rectangle is equal to the area of a parallelogram.
area of parallelogram = base x height square units.
The above-given units:
base = 14 cms
height = 7 cms
Now substitute the values in the formula:
Area = 14 x 7
Area = 98 square cms.

Question 8.

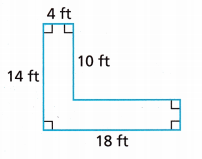
A = ____________
Answer:
The formula to find the area of a rectangle depends on its length and width. The area of a rectangle is calculated in units by multiplying the width (or breadth) by the Length of a rectangle. Lateral and total surface areas can be calculated only for three-dimensional figures. We cannot calculate the rectangle since it is a two-dimensional figure. Thus, the perimeter and the area of a rectangle are given by:
area = length x breadth
Let’s consider base first.
The length is 18

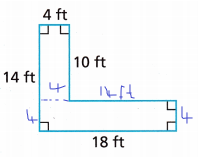
area of one rectangle = 18 x 4
area 1 = 72 square ft.
area of other rectangle = l x b
area2 = 10 x 4
area2 = 40 square ft.
Now add area 1 + area 2
Total area = 72 + 40
Total area = 112 square ft.

Question 9.
The height of a parallelogram is 36 meters and the base is 6 meters. Find the area of the parallelogram.
Answer:
The area of a parallelogram is the region bounded by the parallelogram in a given two-dimension space. To recall, a parallelogram is a special type of quadrilateral which has four sides and the pair of opposite sides are parallel. In a parallelogram, the opposite sides are of equal length and opposite angles are of equal measures. Since the rectangle and the parallelogram have similar properties, the area of the rectangle is equal to the area of a parallelogram.
area of parallelogram = base x height square units.
The above-given units:
base = 6 metres
height = 36 metres
Now substitute the values in the formula:
Area = 36 x 6
Area = 216 square metres.