We included HMH Into Math Grade 5 Answer Key PDF Module 7 Lesson 5 Apply Properties of Addition to make students experts in learning maths.
HMH Into Math Grade 5 Module 7 Lesson 5 Answer Key Apply Properties of Addition
I Can apply the properties of addition to add fractions and mixed numbers.
Step It Out
1. As Pria plays a computer game, the experience bar fills to show her experience level. The bar fills to \(\frac{1}{5}\) before completing a level. After completing the level, the bar fills another \(\frac{3}{5}\). As a bonus, it fills an additional \(\frac{1}{10}\). What is her experience level now?

A. Write an addition expression to model the situation.
\(\frac{1}{5}\) + (___ + ___)
B. Based on the expression you wrote in Part A, how can you use the Commutative Property of Addition, the Associative Property of Addition, or both properties to help you find the sum?
______________________
______________________
C. Use the properties of addition to group the fractions with like denominators together.
___ + ____
D. Find the sum of the fractions in the parentheses.
____ + ____
E. Write equivalent fractions with like denominators.
____ + _____
F. Find the sum. ___________
What is Pria’s experience level now? ________
Answer:
As Pria plays a computer game, the experience bar fills to show her experience level.
The bar fills to \(\frac{1}{5}\) before completing a level.
After completing the level, the bar fills another \(\frac{3}{5}\)
As a bonus, it fills an additional \(\frac{1}{10}\).
\(\frac{1}{5}\) + \(\frac{3}{5}\) + \(\frac{1}{10}\)
\(\frac{4}{5}\) + \(\frac{1}{10}\)
LCD is 10
\(\frac{8}{10}\) + \(\frac{1}{10}\) = \(\frac{9}{10}\)
Turn and Talk How can you estimate to show the sum is reasonable, without evaluating the expression?
Step It Out
2. Add. 1\(\frac{5}{9}\) + 3\(\frac{5}{6}\) + 1\(\frac{2}{9}\)
A. Use the Commutative Property of Addition to put fractions with the same denominator next to each other. _____________
B. Use the Associative Property of Addition and parentheses to group fractions with like denominators together. __________
C. Add the terms located inside the parentheses. ________
D. Write equivalent fractions with like denominators. __________
E. Find the sum. Rename if needed. ________
Answer:
1\(\frac{5}{9}\) + 3\(\frac{5}{6}\) + 1\(\frac{2}{9}\)
1\(\frac{5}{9}\) + 1\(\frac{2}{9}\) + 3\(\frac{5}{6}\)
1 + \(\frac{5}{9}\) + 1 + \(\frac{2}{9}\) + 3 + \(\frac{5}{6}\)
1 + 1 + 3 = 5
\(\frac{5}{9}\) + \(\frac{2}{9}\) + \(\frac{5}{6}\)
\(\frac{7}{9}\) + \(\frac{5}{6}\)
\(\frac{42}{54}\) + \(\frac{45}{54}\) = \(\frac{97}{54}\) = 1 \(\frac{43}{54}\)
5 + 1 \(\frac{43}{54}\) = 6 \(\frac{43}{54}\)
Turn and Talk How are the properties of addition helpful for finding sums of expressions that have three or more addends?
Answer:
The properties of addition make it easier to work with numbers by allowing you to regroup them so that an equation is easier to solve.
Check Understanding Math Board
Question 1.
Michael plans to hike from the ranger station to the mountain top. The map shows the lengths of the different parts of the trail. What is the distance, in miles, from the station to the mountain top?
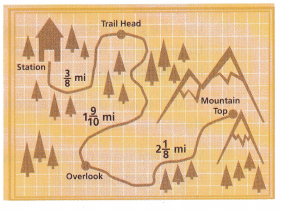
Answer:
\(\frac{3}{8}\) + (1\(\frac{9}{10}\) + 2\(\frac{1}{8}\))
\(\frac{3}{8}\) + (1 + \(\frac{9}{10}\) + 2 + \(\frac{1}{8}\))
3 + \(\frac{3}{8}\) + (\(\frac{9}{10}\) + \(\frac{1}{8}\))
3 + \(\frac{3}{8}\) + (\(\frac{72}{80}\) + \(\frac{10}{80}\))
3 + \(\frac{3}{8}\) + \(\frac{82}{80}\)
3 + \(\frac{30}{80}\) + \(\frac{82}{80}\)
3 + \(\frac{112}{80}\) = 4 \(\frac{2}{5}\)
Add.
Question 2.
\(\frac{3}{5}\) + (\(\frac{1}{2}\) + \(\frac{4}{5}\))
Answer:
\(\frac{3}{5}\) + (\(\frac{1}{2}\) + \(\frac{4}{5}\))
LCD is 10
\(\frac{3}{5}\) + (\(\frac{5}{10}\) + \(\frac{8}{10}\))
\(\frac{3}{5}\) + \(\frac{13}{10}\)
LCD is 10
\(\frac{6}{10}\) + \(\frac{13}{10}\) = \(\frac{19}{10}\) = 1 \(\frac{9}{10}\)
Question 3.
(1\(\frac{1}{4}\) + 1\(\frac{2}{3}\)) + 2\(\frac{2}{3}\)
Answer:
(1\(\frac{1}{4}\) + 1\(\frac{2}{3}\)) + 2\(\frac{2}{3}\)
(1 + \(\frac{1}{4}\) + 1 + \(\frac{2}{3}\)) + 2\(\frac{2}{3}\)
(2 + \(\frac{1}{4}\) + \(\frac{2}{3}\)) + 2\(\frac{2}{3}\)
(2 + \(\frac{3}{12}\) + \(\frac{8}{12}\)) + 2\(\frac{2}{3}\)
2 + \(\frac{11}{12}\) + 2\(\frac{2}{3}\)
2 + \(\frac{11}{12}\) + 2 + \(\frac{2}{3}\)
4 + \(\frac{11}{12}\) + \(\frac{8}{12}\)
4 + \(\frac{19}{12}\) = 4 + 1\(\frac{7}{12}\) = 5\(\frac{7}{12}\)
Question 4.
2\(\frac{5}{8}\) + \(\frac{7}{12}\) + 1\(\frac{5}{8}\)
Answer:
2\(\frac{5}{8}\) + \(\frac{7}{12}\) + 1\(\frac{5}{8}\)
2\(\frac{5}{8}\) + 1\(\frac{5}{8}\) + \(\frac{7}{12}\)
2 + \(\frac{5}{8}\) + 1 + \(\frac{5}{8}\) + \(\frac{7}{12}\)
3 + (\(\frac{5}{8}\) + \(\frac{5}{8}\) + \(\frac{7}{12}\))
3 + (\(\frac{10}{8}\) + \(\frac{7}{12}\))
LCD is 24.
3 + (\(\frac{30}{24}\) + \(\frac{14}{24}\))
3 + \(\frac{44}{24}\) = 3 + \(\frac{11}{6}\)
3 + 1\(\frac{5}{6}\) = 4\(\frac{5}{6}\)
On Your Own
Question 5.
Marcel buys fabric to decorate a set for a school play. He buys 2\(\frac{2}{3}\) yards of green, 3\(\frac{1}{6}\) yards of blue, and 5\(\frac{1}{2}\) yards of black. How much fabric does Marcel buy?
Answer:
Given,
Marcel buys fabric to decorate a set for a school play. He buys 2\(\frac{2}{3}\) yards of green, 3\(\frac{1}{6}\) yards of blue, and 5\(\frac{1}{2}\) yards of black.
(2\(\frac{2}{3}\) + 3\(\frac{1}{6}\)) + 5\(\frac{1}{2}\)/
(2 + \(\frac{2}{3}\) + 3 + \(\frac{1}{6}\)) + 5\(\frac{1}{2}\)
5 + (\(\frac{2}{3}\) + \(\frac{1}{6}\)) + 5\(\frac{1}{2}\)
LCD is 6.
5 + (\(\frac{4}{6}\) + \(\frac{1}{6}\)) + 5\(\frac{1}{2}\)
5 + \(\frac{5}{6}\) + 5\(\frac{1}{2}\)
5 + \(\frac{5}{6}\) + 5 + \(\frac{1}{2}\)
10 + \(\frac{5}{6}\) + \(\frac{1}{2}\)
LCD is 6
\(\frac{5}{6}\) + \(\frac{3}{6}\) = \(\frac{8}{6}\) = 1\(\frac{2}{6}\)
10 + 1\(\frac{2}{6}\) = 11\(\frac{2}{6}\) or 11\(\frac{1}{3}\)
Question 6.
Open Ended Alex writes the expression \(\frac{3}{11}\) + \(\frac{4}{5}\) + \(\frac{6}{11}\) on the board. Explain how you can use the properties of addition to find the sum.
Answer:
\(\frac{3}{11}\) + \(\frac{4}{5}\) + \(\frac{6}{11}\)
\(\frac{3}{11}\) + \(\frac{6}{11}\) + \(\frac{4}{5}\)
\(\frac{9}{11}\) + \(\frac{4}{5}\)
LCD is 55.
\(\frac{45}{55}\) + \(\frac{44}{55}\) = \(\frac{89}{55}\) = 1\(\frac{34}{55}\)
Question 7.
Model with Mathematics The diagram shows the dimensions of a triangular flower bed. Write an addition expression to model the situation. What is the perimeter of the flower bed?

Answer:
(4\(\frac{2}{12}\) + 5\(\frac{5}{6}\)) + 3\(\frac{2}{3}\)
(4\(\frac{1}{6}\) + 5\(\frac{5}{6}\)) + 3\(\frac{2}{3}\)
(4 + \(\frac{1}{6}\) + 5 + \(\frac{5}{6}\)) + 3\(\frac{2}{3}\)
9 + \(\frac{6}{6}\) + 3\(\frac{2}{3}\)
10 + 3\(\frac{2}{3}\) = 13\(\frac{2}{3}\)
So, the perimeter of the flower bed is 13\(\frac{2}{3}\) feet.
Use the properties of addition to find the sum.
Question 8.
\(\frac{1}{7}\) + (\(\frac{2}{7}\) + \(\frac{2}{3}\))
Answer:
\(\frac{1}{7}\) + (\(\frac{2}{7}\) + \(\frac{2}{3}\))
LCD of 7 and 3 is 21.
\(\frac{1}{7}\) + (\(\frac{6}{21}\) + \(\frac{14}{21}\))
\(\frac{1}{7}\) + \(\frac{20}{21}\)
LCD is 21.
\(\frac{3}{21}\) + \(\frac{20}{21}\) = \(\frac{23}{21}\) = 1\(\frac{2}{21}\)
Question 9.
(\(\frac{1}{6}\) + (\(\frac{2}{15}\)) + \(\frac{11}{15}\))
Answer:
(\(\frac{1}{6}\) + (\(\frac{2}{15}\)) + \(\frac{11}{15}\))
\(\frac{1}{6}\) + (\(\frac{13}{15}\)
LCD is 30
\(\frac{5}{30}\) + \(\frac{26}{30}\) = \(\frac{31}{30}\) = 1\(\frac{1}{30}\)
Question 10.
\(\frac{5}{12}\) + \(\frac{1}{3}\) + \(\frac{5}{12}\)
Answer:
\(\frac{5}{12}\) + \(\frac{1}{3}\) + \(\frac{5}{12}\)
\(\frac{10}{12}\) + \(\frac{1}{3}\)
LCD is 12
\(\frac{10}{12}\) + \(\frac{4}{12}\) = \(\frac{14}{12}\) = 1\(\frac{2}{12}\)
Question 11.
(1\(\frac{4}{5}\) + 2\(\frac{3}{4}\)) + 1\(\frac{3}{4}\)
Answer:
(1\(\frac{4}{5}\) + 2\(\frac{3}{4}\)) + 1\(\frac{3}{4}\)
(1 + \(\frac{4}{5}\) + 2 + \(\frac{3}{4}\)) + 1\(\frac{3}{4}\)
(3 + \(\frac{4}{5}\) + \(\frac{3}{4}\)) + 1\(\frac{3}{4}\)
3 + (\(\frac{16}{20}\) + \(\frac{15}{20}\)) + 1\(\frac{3}{4}\)
3 + \(\frac{31}{20}\) + 1\(\frac{3}{4}\)
3 + 1\(\frac{11}{20}\) + 1\(\frac{3}{4}\)
3 + 1 + \(\frac{11}{20}\) + 1 + \(\frac{3}{4}\)
3 + 1 + 1 = 5
\(\frac{11}{20}\) + \(\frac{15}{20}\) = \(\frac{26}{20}\) = 1\(\frac{6}{20}\)
5 + 1\(\frac{6}{20}\) = 6\(\frac{6}{20}\)
Question 12.
3\(\frac{1}{6}\) + 5\(\frac{4}{9}\) + 2\(\frac{1}{6}\)
Answer:
3\(\frac{1}{6}\) + 5\(\frac{4}{9}\) + 2\(\frac{1}{6}\)
(3\(\frac{1}{6}\) + 2\(\frac{1}{6}\)) + 5\(\frac{4}{9}\)
3 + 2 + 5 = 10
10 + (\(\frac{1}{6}\) + \(\frac{1}{6}\)) + \(\frac{4}{9}\)
10 + \(\frac{2}{6}\) + \(\frac{4}{9}\)
\(\frac{2}{6}\) + \(\frac{4}{9}\)
LCD is 18
\(\frac{6}{18}\) + \(\frac{8}{18}\) = \(\frac{14}{18}\) = \(\frac{7}{9}\)
10 + \(\frac{7}{9}\) = 10\(\frac{7}{9}\)
Question 13.
1\(\frac{4}{5}\) + (3\(\frac{2}{5}\) + 2\(\frac{1}{8}\))
Answer:
1\(\frac{4}{5}\) + (3\(\frac{2}{5}\) + 2\(\frac{1}{8}\))
1\(\frac{4}{5}\) + (3 + \(\frac{2}{5}\) + 2 + \(\frac{1}{8}\))
1\(\frac{4}{5}\) + (5 + \(\frac{2}{5}\) + \(\frac{1}{8}\))
5 + 1\(\frac{4}{5}\) + (\(\frac{2}{5}\) + \(\frac{1}{8}\))
5 + 1\(\frac{4}{5}\) + (\(\frac{16}{40}\) + \(\frac{5}{40}\))
5 + 1\(\frac{4}{5}\) + \(\frac{21}{40}\)
Now first add the whole numbers
5 + 1 = 6
\(\frac{32}{40}\) + \(\frac{21}{40}\) = \(\frac{53}{40}\) = 1\(\frac{13}{40}\)
6 + 1\(\frac{13}{40}\) = 7\(\frac{13}{40}\)
Use the properties of addition to find the sum.
Question 14.
(\(\frac{5}{8}\) + 4\(\frac{2}{3}\)) + 1\(\frac{1}{8}\))
Answer:
(\(\frac{5}{8}\) + 4\(\frac{2}{3}\)) + 1\(\frac{1}{8}\))
We can add the fractions by using the associative property.
(\(\frac{5}{8}\) + 4\(\frac{2}{3}\)) + 1\(\frac{1}{8}\))
Rewriting our equation with parts separated
(\(\frac{5}{8}\) + 4 + \(\frac{2}{3}\)) + 1\(\frac{1}{8}\)
LCD is 24.
4 + (\(\frac{5}{8}\) + \(\frac{2}{3}\)) + 1\(\frac{1}{8}\)
4 + \(\frac{31}{24}\)) + 1\(\frac{1}{8}\)
4 + 1\(\frac{7}{24}\)) + 1\(\frac{1}{8}\)
5 \(\frac{7}{24}\) + 1\(\frac{1}{8}\)
5 + \(\frac{7}{24}\) + 1 + \(\frac{1}{8}\)
5 + 1 =6
\(\frac{7}{24}\) + \(\frac{1}{8}\)
LCD is 24
\(\frac{7}{24}\) + \(\frac{3}{24}\) = \(\frac{10}{24}\) = \(\frac{5}{12}\)
6 + \(\frac{5}{12}\) = 6\(\frac{5}{12}\)
Question 15.
4\(\frac{5}{18}\) + \(\frac{3}{4}\) + \(\frac{5}{18}\))
Answer:
4\(\frac{5}{18}\) + \(\frac{3}{4}\) + \(\frac{5}{18}\))
We can add the fractions by using the associative property.
(4\(\frac{5}{18}\) + \(\frac{5}{18}\)) + \(\frac{3}{4}\)
(4 + \(\frac{5}{18}\) + \(\frac{5}{18}\)) + \(\frac{3}{4}\)
4 \(\frac{10}{18}\) + \(\frac{3}{4}\)
4 + \(\frac{10}{18}\) + \(\frac{3}{4}\)
LCD is 36
\(\frac{10}{18}\) + \(\frac{3}{4}\)
\(\frac{20}{36}\) + \(\frac{27}{36}\) = \(\frac{47}{36}\) = 1\(\frac{11}{36}\)
4 + 1\(\frac{11}{36}\) = 5\(\frac{11}{36}\)
Question 16.
\(\frac{7}{10}\) + 2\(\frac{4}{15}\) + 1\(\frac{1}{10}\))
Answer:
\(\frac{7}{10}\) + 2\(\frac{4}{15}\) + 1\(\frac{1}{10}\))
We can add the fractions by using the associative property.
\(\frac{7}{10}\) + (2\(\frac{4}{15}\) + 1\(\frac{1}{10}\))
\(\frac{7}{10}\) + (2 + \(\frac{4}{15}\) + 1 + \(\frac{1}{10}\))
2 + 1 = 3
3 + \(\frac{7}{10}\) + (\(\frac{4}{15}\) + \(\frac{1}{10}\))
3 + \(\frac{4}{15}\) + \(\frac{8}{10}\)
LCD is 30
3 + \(\frac{8}{30}\) + \(\frac{24}{30}\)
3 + \(\frac{32}{30}\)
3 + \(\frac{16}{15}\)
3 + 1\(\frac{1}{15}\) = 4\(\frac{1}{15}\)
Question 17.
Use Structure Valerie writes the expression (\(\frac{1}{12}\) + \(\frac{4}{5}\)) + (\(\frac{1}{5}\) + \(\frac{7}{12}\)). How can she use the properties of addition to rewrite the expression so that it is easier to add?
Answer:
(\(\frac{1}{12}\) + \(\frac{4}{5}\)) + (\(\frac{1}{5}\) + \(\frac{7}{12}\))
LCD is 60.
(\(\frac{5}{60}\) + \(\frac{48}{60}\)) + (\(\frac{12}{5}\) + \(\frac{7}{12}\))
\(\frac{53}{60}\) + \(\frac{19}{60}\) = \(\frac{72}{60}\) = \(\frac{6}{5}\) = 1\(\frac{1}{5}\)
Question 18.
The table shows the portion of three different types of pizzas that Nimal and Peter eat at a team party. All of the pizzas are the same size.
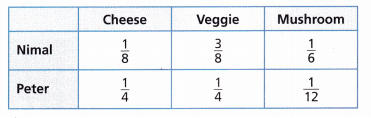
- Who eats more pizza, Nimal or Peter?
- How much more pizza does this boy eat than the other?
Answer:
Amount of pizza Nimal eat = \(\frac{1}{8}\) + \(\frac{3}{8}\) + \(\frac{1}{6}\)
= \(\frac{4}{8}\) + \(\frac{1}{6}\)
= \(\frac{1}{2}\) + \(\frac{1}{6}\)
LCD is 6.
\(\frac{3}{6}\) + \(\frac{1}{6}\) = \(\frac{4}{6}\)
Amount of pizza Peter eat = \(\frac{1}{4}\) + \(\frac{1}{4}\) + \(\frac{1}{12}\)
= \(\frac{2}{4}\) + \(\frac{1}{12}\)
= \(\frac{1}{2}\) + \(\frac{1}{12}\)
LCD is 12.
\(\frac{6}{12}\) + \(\frac{1}{12}\) = \(\frac{7}{12}\)
Nimal eats more pizza than Peter.
Question 19.
Reason Find the sum (2\(\frac{1}{9}\) + 3\(\frac{3}{4}\)) + 3\(\frac{7}{9}\) without using the properties of addition. Would it have been easier to first use the properties of addition to reorder and regroup the addends? Explain your reasoning.
Answer:
(2\(\frac{1}{9}\) + 3\(\frac{3}{4}\)) + 3\(\frac{7}{9}\)
Rewriting our equation with parts separated
(2 + \(\frac{1}{9}\) + 3 + \(\frac{3}{4}\)) + 3\(\frac{7}{9}\)
(5 + \(\frac{1}{9}\) + \(\frac{3}{4}\)) + 3\(\frac{7}{9}\)
LCD is 36
(5 + \(\frac{4}{36}\) + \(\frac{27}{36}\)) + 3\(\frac{7}{9}\)
5\(\frac{31}{36}\)) + 3\(\frac{7}{9}\)
Rewriting our equation with parts separated
5 + \(\frac{31}{36}\) + 3 + \(\frac{7}{9}\)
5 + 3 = 8
\(\frac{31}{36}\) + \(\frac{7}{9}\)
LCD is 36
\(\frac{31}{36}\) + \(\frac{28}{36}\) = \(\frac{59}{36}\)
\(\frac{59}{36}\) = 1\(\frac{23}{36}\)
8 + 1 + \(\frac{23}{36}\) = 9\(\frac{23}{36}\)
It will be easy to use the properties of addition rather than simplifying the expression directly.