We included HMH Into Math Grade 5 Answer Key PDF Module 7 Lesson 4 Rename Mixed Numbers to Subtract to make students experts in learning maths.
HMH Into Math Grade 5 Module 7 Lesson 4 Answer Key Rename Mixed Numbers to Subtract
I Can subtract mixed numbers by renaming.
Step It Out
1. Larry rides his bike to the park. On his way home, he gets a flat tire. How far does Larry have to walk his bike to get home?
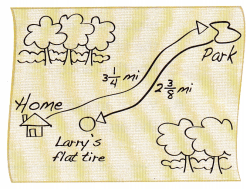
A. Write an expression for the problem.
_____________________
B. Use fraction strips to represent the distance Larry rode to the park as an equivalent fraction with a denominator of 8. Then write a new subtraction expression. _____________________
C. Do you have enough fraction strips to subtract the fractional part of the distance Larry rode home? Explain.
_____________________
D. How can you represent the distance Larry rode to the park using fraction strips so that you are able to subtract the distance Larry rode home before he got a flat tire?
E. Represent the exchange you made with the fraction strips using mixed numbers with an equation and subtract.
F. How far does Larry walk his bike home? _________
Answer:
3\(\frac{1}{4}\) – 2\(\frac{3}{8}\)
Rewriting our equation with parts separated
3 + \(\frac{1}{4}\) – 2 – \(\frac{3}{8}\)
3 – 2 = 1
\(\frac{1}{4}\) – \(\frac{3}{8}\)
\(\frac{2}{8}\) – \(\frac{3}{8}\) = –\(\frac{1}{8}\)
1 – \(\frac{1}{8}\) = \(\frac{7}{8}\)
Turn and Talk How else could you rewrite the mixed numbers 3\(\frac{1}{4}\) and 2\(\frac{3}{8}\) so you can subtract 2\(\frac{3}{8}\)? Explain your reasoning.
Step It Out
2. The students in a fifth-grade class and a fourth-grade class ate some pizza. How many more pizzas did the fifth-graders eat than the fourth-graders?

A. Write an expression to model the problem. ______
B. Estimate the answer. ______
C. Find a common denominator. Use the common denominator to write mixed numbers with equivalent fractions.
______________
D. You can subtract mixed numbers by renaming both numbers as fractions greater than 1. Rename each mixed number.
______________
E. Find the difference. Then rename the difference as a mixed number.
______________
F. How many more pizzas did the fifth-graders eat than the fourth-graders?
______________
G. Is your answer reasonable? Explain.
______________
______________
Answer:
Pizza eaten by the fifth-grade class = 5 \(\frac{1}{6}\)
Pizza eaten by the fourth-grade class = 2 \(\frac{4}{6}\)
5 \(\frac{1}{6}\) – 2 \(\frac{4}{6}\)
Rewriting our equation with parts separated
5 + \(\frac{1}{6}\) – 2 – \(\frac{4}{6}\)
5 – 2 = 3
\(\frac{1}{6}\) – \(\frac{4}{6}\) = –\(\frac{3}{6}\)
3 – \(\frac{3}{6}\) = 2\(\frac{1}{2}\)
Turn and Talk Compare and contrast the method for renaming mixed numbers in this task and the task on the previous page. Which method do you prefer to use? Explain.
3. Sarah measures how much water her horse and donkey each drink. How much more water does the horse drink than the donkey?
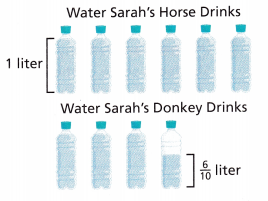
A. What expression can you write to model the problem?
_______________________
B. Can you subtract the fractional part from the whole number? Explain.
_______________________
C. Rename the whole number to subtract and explain the process you use.
_______________________
D. Find the difference. _______________________
E. How much more water does the horse drink than the donkey?
_______________________
Answer:
Sarah measures how much water her horse and donkey each drink.
Water Sarah’s Horse drink = 1
Water Sarah’s Donkey drink = \(\frac{6}{10}\)
1 – \(\frac{6}{10}\)
\(\frac{10}{10}\) – \(\frac{6}{10}\) = \(\frac{4}{10}\)
Horse drink \(\frac{4}{10}\) liter than donkey.
Check Understanding Math Board
Question 1.
Marcus has a board that is 7\(\frac{1}{4}\) feet long. If he cuts off a piece that is 2\(\frac{1}{2}\) feet long, how long will the board be?
Answer:
Given,
Marcus has a board that is 7\(\frac{1}{4}\) feet long.
7\(\frac{1}{4}\) – 2\(\frac{1}{2}\)
Rewriting our equation with parts separated
7 + \(\frac{1}{4}\) – 2 – \(\frac{1}{2}\)
7 – 2 = 5
\(\frac{1}{4}\) – \(\frac{1}{2}\)
LCD is 4.
\(\frac{1}{4}\) – \(\frac{2}{4}\) = –\(\frac{1}{4}\)
5 – \(\frac{1}{4}\) = 4\(\frac{3}{4}\)
Estimate. Then find the difference.
Question 2.
4\(\frac{1}{3}\) – 2\(\frac{5}{6}\) _________
Answer:
4\(\frac{1}{3}\) – 2\(\frac{5}{6}\)
Rewriting our equation with parts separated
4 + \(\frac{1}{3}\) – 2 – \(\frac{5}{6}\)
4 – 2 = 2
\(\frac{1}{3}\) – \(\frac{5}{6}\)
LCD is 6.
\(\frac{2}{6}\) – \(\frac{5}{6}\) = –\(\frac{3}{6}\) = –\(\frac{1}{2}\)
2 – \(\frac{1}{2}\) = 1\(\frac{1}{2}\)
Estimated difference is 1\(\frac{1}{2}\)
Actual difference is 1\(\frac{1}{2}\)
Question 3.
5\(\frac{1}{4}\) – 1\(\frac{1}{3}\) _________
Answer:
5\(\frac{1}{4}\) – 1\(\frac{1}{3}\)
Rewriting our equation with parts separated
5 + \(\frac{1}{4}\) – 1 – \(\frac{1}{3}\)
5 – 1 = 4
\(\frac{1}{4}\) – \(\frac{1}{3}\)
LCD is 12
\(\frac{3}{12}\) – \(\frac{4}{12}\) = –\(\frac{1}{12}\)
4 – \(\frac{1}{12}\)
3\(\frac{12}{12}\) – \(\frac{1}{12}\) = 3\(\frac{11}{12}\)
Estimated difference is 4
Actual difference is 3\(\frac{11}{12}\)
On Your Own
Question 4.
Reason Bethany has 3\(\frac{3}{8}\) pounds of peanuts in a bag. She feeds some of the peanuts to squirrels. How many pounds of peanuts does Bethany feed to the squirrels?

- Estimate the difference.
____________________ - How many pounds of peanuts does she feed to the squirrels?
____________________ - Is your answer reasonable? Explain.
____________________
Answer:
Given,
Bethany has 3\(\frac{3}{8}\) pounds of peanuts in a bag. She feeds some of the peanuts to squirrels.
3\(\frac{3}{8}\) – 1\(\frac{13}{16}\)
Rewriting our equation with parts separated
3 + \(\frac{3}{8}\) – 1 – \(\frac{13}{16}\)
3 – 1 = 2
\(\frac{3}{8}\) – \(\frac{13}{16}\)
LCD is 16.
\(\frac{6}{16}\) – \(\frac{13}{16}\) = –\(\frac{7}{16}\)
2 – \(\frac{7}{16}\) = 1\(\frac{9}{16}\)
Estimated difference is 1\(\frac{1}{2}\)
Bethany feed 1\(\frac{9}{16}\) pounds of peanuts to squirrels.
Estimate. Then find the difference.
Question 5.
5\(\frac{1}{3}\) – 1\(\frac{7}{8}\)
Answer:
5\(\frac{1}{3}\) – 1\(\frac{7}{8}\)
Rewriting our equation with parts separated
5 + \(\frac{1}{3}\) – 1 – \(\frac{7}{8}\)
5 – 1 = 4
\(\frac{1}{3}\) – \(\frac{7}{8}\)
LCD is 24.
\(\frac{8}{24}\) – \(\frac{21}{24}\) = –\(\frac{13}{24}\)
4 – \(\frac{13}{24}\) = 3\(\frac{11}{24}\)
Estimated difference is 3
Actual difference is 3\(\frac{11}{24}\)
Question 6.
3\(\frac{1}{4}\) – 2\(\frac{4}{5}\)
Answer:
3\(\frac{1}{4}\) – 2\(\frac{4}{5}\)
Rewriting our equation with parts separated
3 + \(\frac{1}{4}\) – 2 – \(\frac{4}{5}\)
3 – 2 = 1
\(\frac{1}{4}\) – \(\frac{4}{5}\)
LCD is 20.
\(\frac{5}{20}\) – \(\frac{16}{20}\) = –\(\frac{11}{20}\)
1 – \(\frac{11}{20}\) = \(\frac{9}{20}\)
Estimated difference is \(\frac{1}{2}\)
Actual difference is \(\frac{9}{20}\)
Question 7.
6\(\frac{1}{2}\) – 4\(\frac{9}{10}\)
Answer:
6\(\frac{1}{2}\) – 4\(\frac{9}{10}\)
Rewriting our equation with parts separated
6 + \(\frac{1}{2}\) – 4 – \(\frac{9}{10}\)
6 – 4 = 2
\(\frac{1}{2}\) – \(\frac{9}{10}\)
LCD is 10.
\(\frac{5}{10}\) – \(\frac{9}{10}\) = –\(\frac{4}{10}\) = –\(\frac{2}{5}\)
2 – \(\frac{2}{5}\)
1\(\frac{5}{5}\) – \(\frac{2}{5}\) = 1\(\frac{3}{5}\)
Estimated difference is 2
Actual difference is 1\(\frac{3}{5}\)
Question 8.
8\(\frac{1}{3}\) – 2\(\frac{5}{6}\)
Answer:
8\(\frac{1}{3}\) – 2\(\frac{5}{6}\)
Rewriting our equation with parts separated
8 + \(\frac{1}{3}\) – 2 – \(\frac{5}{6}\)
8 – 2 = 6
\(\frac{1}{3}\) – \(\frac{5}{6}\)
LCD is 6.
\(\frac{2}{6}\) – \(\frac{5}{6}\) = –\(\frac{3}{6}\) = –\(\frac{1}{2}\)
6 – \(\frac{1}{2}\) = 5\(\frac{1}{2}\)
Estimated difference is 6
Actual difference is 5\(\frac{1}{2}\)
Question 9.
9\(\frac{3}{8}\) – 3\(\frac{1}{2}\)
Answer:
9\(\frac{3}{8}\) – 3\(\frac{1}{2}\)
Rewriting our equation with parts separated
9 + \(\frac{3}{8}\) – 3 – \(\frac{1}{2}\)
9 – 3 = 6
\(\frac{3}{8}\) – \(\frac{1}{2}\)
LCD is 8.
\(\frac{3}{8}\) – \(\frac{4}{8}\) = –\(\frac{1}{8}\)
6 – \(\frac{1}{8}\)
5\(\frac{8}{8}\) – \(\frac{1}{8}\) = 5\(\frac{7}{8}\)
Estimated difference is 6
Actual difference is 5\(\frac{7}{8}\)
Question 10.
11 – 8\(\frac{1}{12}\)
Answer:
11 – 8\(\frac{1}{12}\)
11 – 8 = 3
3 – \(\frac{1}{12}\)
2 \(\frac{12}{12}\) – \(\frac{1}{12}\)
2\(\frac{11}{12}\)
11 – 8\(\frac{1}{12}\) = 2\(\frac{11}{12}\)
Estimated difference is 3
Actual difference is 2\(\frac{11}{12}\)
Question 11.
Franco practices the piano for 4\(\frac{1}{2}\) hours each week. He plays soccer for 1\(\frac{3}{4}\) hours. How much longer does Franco practice piano than play soccer?
Answer:
Franco practices the piano for 4\(\frac{1}{2}\) hours each week.
He plays soccer for 1\(\frac{3}{4}\) hours.
4\(\frac{1}{2}\) – 1\(\frac{3}{4}\)
Rewriting our equation with parts separated
4 – 1 = 3
\(\frac{1}{2}\) – \(\frac{3}{4}\)
LCD is 4.
\(\frac{2}{4}\) – \(\frac{3}{4}\) = –\(\frac{1}{4}\)
3 – \(\frac{1}{4}\) = 2\(\frac{3}{4}\)
Franco practice piano 2\(\frac{3}{4}\) hours than soccer.
Question 12.
Hannah grows two corn plants. The first plant is 6\(\frac{1}{4}\) feet tall. The second plant is 4\(\frac{6}{8}\) feet tall. How much taller is the first corn plant?
Answer:
Given,
Hannah grows two corn plants. The first plant is 6\(\frac{1}{4}\) feet tall.
The second plant is 4\(\frac{6}{8}\) feet tall.
6\(\frac{1}{4}\) – 4\(\frac{6}{8}\)
Rewriting our equation with parts separated
6 + \(\frac{1}{4}\) – 4 – \(\frac{6}{8}\)
6 – 4 = 2
\(\frac{1}{4}\) – \(\frac{6}{8}\)
\(\frac{2}{8}\) – \(\frac{6}{8}\) = –\(\frac{4}{8}\) = –\(\frac{1}{2}\)
2 – \(\frac{1}{2}\) = 1\(\frac{1}{2}\)
The first corn plant is 1\(\frac{1}{2}\) feet taller than second plant.
Question 13.
Critique Reasoning Cata walks the long way to school. On her way home, she takes a shortcut. Cata says the shortcut saves at least 1 mile. Is Cata’s reasoning correct? Explain.
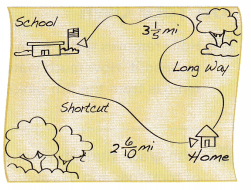
Answer:
Distance from home to school = 3\(\frac{1}{5}\)
Shortcut distance from home to school = 2\(\frac{6}{10}\)
3\(\frac{1}{5}\) – 2\(\frac{6}{10}\)
Rewriting our equation with parts separated
3 – 2 = 1
\(\frac{1}{5}\) – \(\frac{6}{10}\)
LCD is 10.
\(\frac{2}{10}\) – \(\frac{6}{10}\) = –\(\frac{4}{10}\) = –\(\frac{2}{5}\)
1 – \(\frac{2}{5}\) = \(\frac{3}{5}\)
\(\frac{3}{5}\) < 1
So, Cata’s reasoning is incorrect.
Question 14.
Model with Mathematics Thomas watched two movies this weekend. Cenozoic World lasted 2\(\frac{1}{6}\) hours. Happy Robots lasted 1\(\frac{3}{4}\) hours. How many hours longer was Cenozoic World than Happy Robots? Write an expression to model the problem. Then solve.
Answer:
Given,
Thomas watched two movies this weekend. Cenozoic World lasted 2\(\frac{1}{6}\) hours.
Happy Robots lasted 1\(\frac{3}{4}\) hours.
2\(\frac{1}{6}\) – 1\(\frac{3}{4}\)
Rewriting our equation with parts separated
2 – 1 = 1
\(\frac{1}{6}\) – \(\frac{3}{4}\)
LCD is 12
\(\frac{2}{12}\) – \(\frac{9}{12}\) = –\(\frac{7}{12}\)
1 – \(\frac{7}{12}\) = \(\frac{5}{12}\)
Thus \(\frac{5}{12}\) hours longer was Cenozoic World than Happy Robots.
Estimate. Then find the difference.
Question 15.
4\(\frac{1}{3}\) – 2\(\frac{4}{5}\)
Answer:
Rewriting our equation with parts separated
4\(\frac{1}{3}\) – 2\(\frac{4}{5}\)
4 + \(\frac{1}{3}\) – 2 – \(\frac{4}{5}\)
4 – 2 = 2
\(\frac{1}{3}\) – \(\frac{4}{5}\)
LCD is 15.
\(\frac{5}{15}\) – \(\frac{12}{15}\) = –\(\frac{7}{15}\)
2 – \(\frac{7}{15}\) = 1\(\frac{8}{15}\)
Question 16.
3\(\frac{1}{3}\) – 1\(\frac{6}{9}\)
Answer:
3\(\frac{1}{3}\) – 1\(\frac{6}{9}\)
Rewriting our equation with parts separated
3 + \(\frac{1}{3}\) – 1 – \(\frac{6}{9}\)
3 – 1 = 2
\(\frac{1}{3}\) – \(\frac{6}{9}\)
\(\frac{1}{3}\) – \(\frac{2}{3}\) = –\(\frac{1}{3}\)
2 – \(\frac{1}{3}\)
1\(\frac{3}{3}\) – \(\frac{1}{3}\) = 1\(\frac{2}{3}\)
Question 17.
10 – 5\(\frac{7}{8}\)
Answer:
10 – 5\(\frac{7}{8}\)
Rewriting our equation with parts separated
10 – 5 – \(\frac{7}{8}\)
10 – 5 = 5
5 – \(\frac{7}{8}\)
4\(\frac{8}{8}\) – \(\frac{7}{8}\) = 3\(\frac{1}{8}\)
Question 18.
6\(\frac{1}{3}\) – 3\(\frac{2}{4}\)
Answer:
6\(\frac{1}{3}\) – 3\(\frac{2}{4}\)
Rewriting our equation with parts separated
6 + \(\frac{1}{3}\) – 3 – \(\frac{2}{4}\)
6 – 3 = 3
\(\frac{1}{3}\) – \(\frac{2}{4}\)
Simplify the fractions
\(\frac{1}{3}\) – \(\frac{1}{2}\)
LCD is 6.
\(\frac{2}{6}\) – \(\frac{3}{6}\) = – \(\frac{1}{6}\)
3 – \(\frac{1}{6}\)
2\(\frac{6}{6}\) – \(\frac{1}{6}\) = 2\(\frac{5}{6}\)
Question 19.
8\(\frac{2}{3}\) – 3\(\frac{11}{12}\)
Answer:
8\(\frac{2}{3}\) – 3\(\frac{11}{12}\)
Rewriting our equation with parts separated
8 + \(\frac{2}{3}\) – 3 – \(\frac{11}{12}\)
8 – 3 = 5
\(\frac{2}{3}\) – \(\frac{11}{12}\)
LCD is 12
\(\frac{8}{12}\) – \(\frac{11}{12}\) = –\(\frac{3}{12}\)
5 – \(\frac{3}{12}\)
4\(\frac{12}{12}\) – \(\frac{3}{12}\) = 4\(\frac{9}{12}\)
Question 20.
16 – 7\(\frac{5}{12}\)
Answer:
16 – 7\(\frac{5}{12}\)
Rewriting our equation with parts separated
16 – 7 – \(\frac{5}{12}\)
16 – 7 = 9
9 – \(\frac{5}{12}\)
8\(\frac{12}{12}\) – \(\frac{5}{12}\) = 8\(\frac{7}{12}\)
Question 21.
Keshawn runs 6\(\frac{3}{8}\) laps around a track. Mark runs 3\(\frac{3}{4}\) laps around the track. How many more laps does Keshawn run than Mark?
Answer:
Given,
Keshawn runs 6\(\frac{3}{8}\) laps around a track.
Mark runs 3\(\frac{3}{4}\) laps around the track.
6\(\frac{3}{8}\) – 3\(\frac{3}{4}\)
Rewriting our equation with parts separated
6 + \(\frac{3}{8}\) – 3 – \(\frac{3}{4}\)
6 – 3 = 3
\(\frac{3}{8}\) – \(\frac{3}{4}\)
\(\frac{3}{8}\) – \(\frac{6}{8}\) = –\(\frac{3}{8}\)
3 – \(\frac{3}{8}\) = 2\(\frac{5}{8}\)
Question 22.
Ryan rakes leaves for 3 hours. The time he spends raking leaves is 1\(\frac{1}{4}\) hours more than the time he spends playing basketball. How long does Ryan play basketball?
Answer:
Given,
Ryan rakes leave for 3 hours. The time he spends raking leaves is 1\(\frac{1}{4}\) hours more than the time he spends playing basketball.
3 – 1\(\frac{1}{4}\)
Rewriting our equation with parts separated
3 – 1 – \(\frac{1}{4}\)
3 – 1 = 2
2 – \(\frac{1}{4}\) = 1\(\frac{3}{4}\)
Thus Ryan play basketball for 1\(\frac{3}{4}\) hours.
On Your Own
Question 23.
Holly removes water from a fish tank to clean it. How much water does Holly remove from the fish tank?
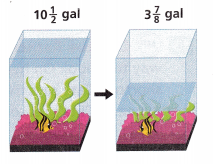
Answer:
10\(\frac{1}{2}\) – 3\(\frac{7}{8}\)
Rewriting our equation with parts separated
10 + \(\frac{1}{2}\) – 3 – \(\frac{7}{8}\)
10 – 3 = 7
\(\frac{1}{2}\) – \(\frac{7}{8}\)
LCD is 8.
\(\frac{4}{8}\) – \(\frac{7}{8}\) = –\(\frac{3}{8}\)
7 – \(\frac{3}{8}\) = 6\(\frac{5}{8}\)
Question 24.
Fifth-grade students plant a class garden. They plant 7\(\frac{1}{6}\) rows of tomatoes and 3\(\frac{1}{2}\) rows of carrots. How many fewer rows of carrots than rows of tomatoes do the students plant?
Answer:
Given,
Fifth-grade students plant a class garden. They plant 7\(\frac{1}{6}\) rows of tomatoes and 3\(\frac{1}{2}\) rows of carrots.
7\(\frac{1}{6}\) – 3\(\frac{1}{2}\)
Rewriting our equation with parts separated
7 + \(\frac{1}{6}\) – 3 – \(\frac{1}{2}\)
7 – 3 = 4
\(\frac{1}{6}\) – \(\frac{1}{2}\)
LCD is 6.
\(\frac{1}{6}\) – \(\frac{3}{6}\) = –\(\frac{2}{6}\)
4 – \(\frac{2}{6}\) = 3\(\frac{2}{3}\)
Question 25.
Model with Mathematics Jae needs 4\(\frac{1}{4}\) cups of flour to make two pizzas for dinner. He has 2\(\frac{1}{2}\) cups of flour. How many more cups of flour does he need? Write an expression to model the problem. Then solve.
Answer:
Given,
Jae needs 4\(\frac{1}{4}\) cups of flour to make two pizzas for dinner.
He has 2\(\frac{1}{2}\) cups of flour.
4\(\frac{1}{4}\) – 2\(\frac{1}{2}\)
Rewriting our equation with parts separated
4 + \(\frac{1}{4}\) – 2 – \(\frac{1}{2}\)
4 – 2 = 2
\(\frac{1}{4}\) – \(\frac{1}{2}\) =- \(\frac{1}{4}\)
2 – \(\frac{1}{4}\) = 1 \(\frac{3}{4}\)
Thus Jae needs 1 \(\frac{3}{4}\) cups of flour.
Question 26.
Reason A weather balloon is 3\(\frac{1}{10}\) miles above the ground. Later, it is 1\(\frac{3}{5}\) miles above the ground.
- How far did the balloon descend?

- How do you know your answer is reasonable?
Answer:
Given,
A weather balloon is 3\(\frac{1}{10}\) miles above the ground.
Later, it is 1\(\frac{3}{5}\) miles above the ground.
3\(\frac{1}{10}\) – 1\(\frac{3}{5}\)
Rewriting our equation with parts separated
3 + \(\frac{1}{10}\) – 1 – \(\frac{3}{5}\)
3 – 1 = 2
\(\frac{1}{10}\) – \(\frac{3}{5}\)
LCD is 10.
\(\frac{1}{10}\) – \(\frac{6}{10}\) = –\(\frac{1}{2}\)
2 – \(\frac{1}{2}\) = 1\(\frac{1}{2}\)
Thus the balloon decends 1\(\frac{1}{2}\) miles.
Question 27.
Construct Arguments Ms. Hendricks buys 4\(\frac{1}{4}\) yards of fabric. She uses 2\(\frac{1}{2}\) yards of the fabric to make a curtain. She needs 1\(\frac{3}{4}\) yards of fabric to cover a footrest. Does Ms. Hendricks have enough fabric to cover the footrest? Explain.
Answer:
Given,
Ms. Hendricks buys 4\(\frac{1}{4}\) yards of fabric.
She uses 2\(\frac{1}{2}\) yards of the fabric to make a curtain. She needs 1\(\frac{3}{4}\) yards of fabric to cover a footrest.
2\(\frac{1}{2}\) + 1\(\frac{3}{4}\)
2 + \(\frac{1}{2}\) + 1 + \(\frac{3}{4}\)
2 + 1 = 3
\(\frac{1}{2}\) + \(\frac{3}{4}\)
\(\frac{2}{4}\) + \(\frac{3}{4}\) = \(\frac{5}{4}\) = 1\(\frac{1}{4}\)
3 + 1\(\frac{1}{4}\) = 4\(\frac{1}{4}\)
So, yes Ms. Hendricks have enough fabric to cover the footrest.