Into Math Grade 5 Module 6 Answer Key Understand Addition and Subtraction of Fractions with Unlike Denominators

We included HMH Into Math Grade 5 Answer Key PDF Module 6 Understand Addition and Subtraction of Fractions with Unlike Denominators to make students experts in learning maths.

HMH Into Math Grade 5 Module 6 Answer Key Understand Addition and Subtraction of Fractions with Unlike Denominators

Fashion Designer

Many fashion designers have an eye for design and detail. They make many types of clothing.
Designers sketch their ideas, and they choose colors, patterns, and fabrics to complement the design. They also collaborate with others to make the products.

Many fashion designers in the United States work in New York and California.
To be a successful fashion designer, you need to have artistic, communication, and computer skills.

Fashion designers design accessories too—like handbags, ties, and shoes.

STEM Task:
Design a fabric pattern that you can describe using fractions such as \(\frac{1}{4}\) of the shapes are green,” or “\(\frac{1}{3}\) of the shapes are squares.” Draw a simple shape, such as a leaf, on an index card. Carefully cut it out. Use the shape as a template and trace it multiple times on a sheet of paper. Make additional templates to add other shapes to your design. Color your design any way you choose.

Learning Mindset!
Challenge-Seeking Defines Own Challenges

Believing in yourself is important, but so is making a plan and not giving up. Set realistic goals and know that the challenge may not be immediately achieved. By defining your own challenges, you can focus on the work that needs to be done to achieve your goals. Then you can find a new challenge. How did you challenge yourself when you made your fabric design? We often adjust challenges in tasks to keep them interesting. If a task is too easy, you can get bored. If it’s too hard, you can get frustrated. Sometimes you need to adjust your work on a task to keep it engaging.

Reflect

Question.
Did you challenge yourself to come up with an interesting design?
Answer:

Question.
What types of challenges interest you the most?

What Fraction is Each Puzzle Piece?

• What fraction of the whole square does each puzzle piece represent?
  Orange triangle: ____ Yellow triangle: ____
  Light blue triangle: ____ Aqua square: _____
  Green triangle: ____ Pink parallelogram: ____
  Dark blue triangle: ____
  

Answer:
Orange triangle: 1/7 Yellow triangle: 1/7
Light blue triangle: 1/7 Aqua square: 1/7
Green triangle: 1/7 Pink parallelogram: 1/7
Dark blue triangle: 1/7

Turn and Talk

• How can you draw lines to help determine the fractions?
• Predict the sum of your fractions. Explain how you know.
• What two pieces can be used to represent \(\frac{1}{2}\)? Explain how you know.

Are You Ready?

Complete these problems to review prior concepts and skills you will need for this module.

Part of a Whole

Write the fraction that names the equal part. Then write a fraction to name the shaded part of the whole.

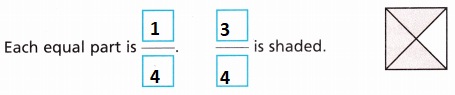
Question 1.

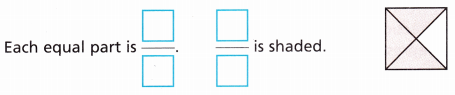
Answer:
The name of the shape is square.
It is divided into 4 equal parts.
Each equal part is 1/4.
3 parts are shaded. So, the fraction of the shaded part is 3/4.

Question 2.

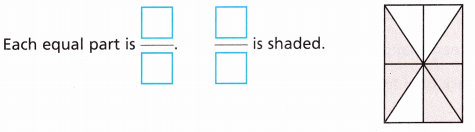
Answer:
The name of the shape is a rectangle.
It is divided into 8 equal parts.
Each equal part is 1/8.
5 parts are shaded. So, the fraction of the shaded part is 5/8.

Add and Subtract Fractions

Find the sum or difference.

Question 3.
\(\frac{3}{8}\) + \(\frac{3}{8}\) = ___
Answer:
\(\frac{3}{8}\) + \(\frac{3}{8}\)
The denominators of the fractions are the same so add the numerators.
\(\frac{3}{8}\) + \(\frac{3}{8}\) = \(\frac{6}{8}\) = \(\frac{3}{4}\)

Question 4.
\(\frac{5}{9}\) – \(\frac{2}{9}\) = ___
Answer:
\(\frac{5}{9}\) – \(\frac{2}{9}\)
The denominators of the fractions are the same so subtract the numerators.
\(\frac{5}{9}\) – \(\frac{2}{9}\) = \(\frac{3}{9}\) = \(\frac{1}{9}\)

Question 5.
\(\frac{1}{6}\) + \(\frac{5}{6}\) = ___
Answer:
\(\frac{1}{6}\) + \(\frac{5}{6}\)
The denominators of the fractions are same so add the numerators.
\(\frac{1}{6}\) + \(\frac{5}{6}\) = \(\frac{6}{6}\) = 1

Question 6.
\(\frac{2}{5}\) + \(\frac{1}{5}\) = ___
Answer:
\(\frac{2}{5}\) + \(\frac{1}{5}\)
The denominators of the fractions are same so add the numerators.
\(\frac{2}{5}\) + \(\frac{1}{5}\) = \(\frac{3}{5}\)

Question 7.
\(\frac{1}{3}\) + \(\frac{1}{3}\) = ___
Answer:
\(\frac{1}{3}\) + \(\frac{1}{3}\)
The denominators of the fractions are same so add the numerators.
\(\frac{1}{3}\) + \(\frac{1}{3}\) = \(\frac{2}{3}\)

Question 8.
\(\frac{4}{7}\) – \(\frac{2}{7}\) = ___
Answer:
\(\frac{4}{7}\) – \(\frac{2}{7}\)
The denominators of the fractions are same so subtract the numerators.
\(\frac{4}{7}\) – \(\frac{2}{7}\) = \(\frac{2}{7}\)

Question 9.
\(\frac{3}{4}\) – \(\frac{1}{4}\) = ___
Answer:
\(\frac{3}{4}\) – \(\frac{1}{4}\)
The denominators of the fractions are same so subtract the numerators.
\(\frac{3}{4}\) – \(\frac{1}{4}\) = \(\frac{2}{4}\) = \(\frac{1}{2}\)

Question 10.
\(\frac{7}{8}\) – \(\frac{5}{8}\) = ___
Answer:
\(\frac{7}{8}\) – \(\frac{5}{8}\)
The denominators of the fractions are same so subtract the numerators.
\(\frac{7}{8}\) – \(\frac{5}{8}\)  = \(\frac{2}{8}\) = \(\frac{1}{4}\)

Question 11.
\(\frac{4}{9}\) + \(\frac{1}{9}\) = ___
Answer:
\(\frac{4}{9}\) + \(\frac{1}{9}\)
The denominators of the fractions are same so add the numerators.
\(\frac{4}{9}\) + \(\frac{1}{9}\) = \(\frac{5}{9}\)

Multiples

Write the first six nonzero multiples.

Question 12.
2 _______
Answer:
The first six nonzero multiples of 2 are 2, 4, 6, 8, 12, 14.

Question 13.
9 ___________
Answer:
The first six nonzero multiples of 9 are 9, 18, 27, 36, 45, 54.

Question 14.
8 _______
Answer:
The first six nonzero multiples of 8 are 8, 16, 24, 32, 48, and 56.

Question 15.
4 ___________
Answer:
The first six nonzero multiples of 4 are 4, 8, 12, 16, 24, 28.

Question 16.
6 ___________
Answer:
The first six nonzero multiples of 6 are 6, 12, 18, 24, 36, 42.

Question 17.
3 ___________
Answer:
The first six nonzero multiples of 3 are 3, 6, 9, 12, 15, 18.