We included HMH Into Math Grade 5 Answer Key PDF Module 5 Lesson 6 Find Volume of Composed Figures to make students experts in learning maths.
HMH Into Math Grade 5 Module 5 Lesson 6 Answer Key Find Volume of Composed Figures
I Can find the volume of a figure composed of right rectangular prisms.
Step It Out
1. Braydon builds a frame in the shape shown. He plans to pour concrete into his frame.
A. Write the unknown dimensions of the composed figure. Describe how you found your answers.
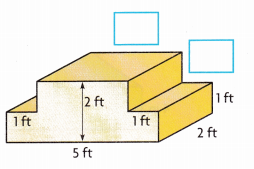
________________________
________________________
B. Draw a line to show how you can break apart Braydon’s frame into two right rectangular prisms, and then find the volume of each prism. Describe your answer.
________________________
________________________
________________________
C. What is the amount of concrete that Braydon needs? Describe how you found your answer.
________________________
________________________
________________________
Answer:
A.Dimensions of base rectangular prism are length 5 ft, width 2 ft and height 1 ft is
The dimensions of top rectangular prism are length 3 ft, width 2 ft and height is 1 ft,
B. 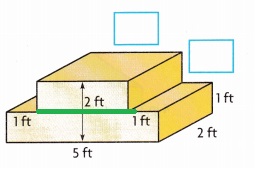
Volume of base prism is 10 cubic ft,
volume of top prism is 6 cubic ft,
C. The amount of concrete that Braydon needed is 16 cubic ft,
Explanation:
Given Braydon builds a frame in the shape shown. He plans to pour concrete into his frame.
A. The unknown dimensions of the composed figure are
we divide into 2 rectangular prisms, the dimensions of base rectangular prisim are length 5 ft, width 2 ft and height 1 ft is
The dimensions of top rectangular prism is length 3 ft, width 2 ft and height is 1 ft.
B. Drawn a line with green color to show how I can break apart Braydon’s frame into two right rectangular prisms and then find the volume of each prism as base prism volume = 5 ft X 2 ft X 1 ft = 10 cubic ft, top prism volume = 3 ft X 2 ft X 1 ft = 6 cubic ft.
C. The amount of concrete that Braydon needed is
base volume + top volume = 10 cubic ft + 6 cubic ft =
16 cubic ft, by adding both top and bottom volumes.
Turn and Talk Is there another way to break apart the frame into right rectangular prisms? Explain.
Answer:
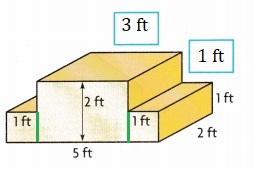
Explanation:
As shown above another way to break apart the frame into right rectangular prisms we can make 3 rectangular prisms with dimensions
1. 1 ft X 2 ft X 1 ft,
2. 3 ft X 2 ft X 1 ft and
3. 1 ft X 2 ft X 1 ft.
Step It Out
2. Tori wants to use the design shown to build steps from solid blocks of wood, Find the amount of wood she needs to build the steps.
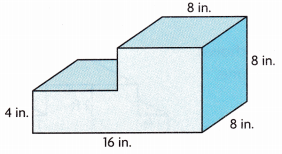
A. Draw a line to show how you can break apart Tori’s design into two right rectangular prisms, and then find the length, width, and height of each right rectangular prism.
_______________________________
B. What is the volume of each of your rectangular prisms?
_______________________________
C. Write an equation to model the amount of wood that Tori needs to build the steps.
_______________________________
D. What is the amount of wood that Tori needs to build the steps? ________
E. Describe how you can check your answer using unit cubes.
________________________
________________________
Answer:
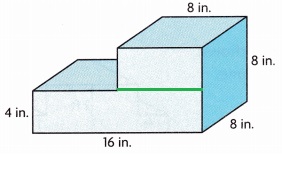
Base prism length is 16 in, width 8 in and height 4 in,
Top prism length is 8 in, width 8 in height 4 in,
B. Volume of base prism is 512 cubic in,
Volume of top prism is 256 cubic in,
C. Equation: (16 in X 8 in X 4 in) + (8 in X 8 in X 4 in)
D. The amount of wood that Tori needs to build the steps is 768 cubic in,
E. 768 unit cubes,
Explanation:
Given Tori wants to use the design shown to build steps from solid blocks of wood,
A. Drawn a line to show how I can break apart Tori’s design into two right rectangular prism and then find the length, width, and height of each right rectangular prism is base prism
length is 16 in, width 8 in and height 4 in, top prism length is 8 in, width 8 in, height 4 in.
B. The volume of each of my rectangular prisms are
base volume = 16 in X 8 in X 4 in = 512 cubic in.
top volume = 8 in X 8 in X 4 in = 256 cubic in.
C. Equation to model the amount of wood that Tori needs to build the steps is
(16 in X 8 in X 4 in) + (8 in X 8 in X 4 in),
D. The amount of wood that Tori needs to build the steps is (16 in X 8 in X 4 in) + (8 in X 8 in X 4 in) =
512 cubic in + 256 cubic in,
768 cubic in.
E. To check my answer using unit cubes is we divide by 1 cubic in we get as unit cubes as
768 cubic in ÷ 1 cubic in X 1 unit cubes = 768 unit cubes.
Turn and Talk Suppose Tori wants to make steps by cutting out wood in the shape of a right rectangular prism from a single block of wood. What could be the dimensions of the single block of wood?
Answer:
16 in X 8 in X 6 in or 12 in X 8 in X 8 in,
Explanation:
If Tori wants to make steps by cutting out wood in the shape of a right rectangular prism from a single block of wood. As the volume is 768 cubic in the dimensions of the single block of wood can be
16 in X 8 in X 6 in = 768 cubic in or
12 in X 8 in X 8 in = 768 cubic in.
3. Consider the space shown above Tori’s bottom step.
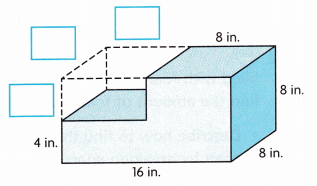
A. Write the dimensions of the space above the bottom step, and then find the volume of the space.
_____________________________
B. If the space and the steps are combined, they form a right rectangular prism. What are the dimensions of the prism, and what is its volume?
_____________________________
_____________________________
C. What is the volume when you subtract the volume of the space from the volume of the prism? What does it represent?
_____________________________
Answer:
A. 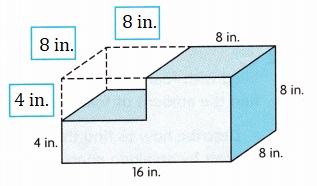
Volume = 256 cubic in,
B. Combined right rectangular prism dimensions are length is 16 in, width 8 in and height 8 in and volume is 1,024 cubic in,
C. The volume when we subtract the volume of the space from the volume of the prism is 768 cubic in, Tori’s volume of the given shape,
Explanation:
Considering the space shown above Tori’s bottom step
A. Wrote the dimensions of the space above the bottom step and the volume of the space is as length is 8 in, width 8 in and height 4 in is
V = 8 in X 8 in X 4 in = 256 cubic in,
B. If the space and the steps are combined, they form a right rectangular prism.
The dimensions of the prism are length is 16 in, width 8 in and height 8 in and its volume is 16 in X 8 in X 8 in = 1,024 cubic in.
C. The volume when I subtract the volume of the space from the volume of the prism is
1,024 cubic in – 256 cubic in = 768 cubic in it represents
Tori’s volume of given shape.
Turn and Talk Describe two ways to find the volume of a composed figure.
Answer:
1 way:
Volume of total prism with space minus volume of the space,
2 way:
Volumes of separated prims top and bottom and adding,
Explanation:
Two ways to find the volume of a composed figure is
1 way :
Calculating the volume as volume of total prism with space minus volume of the space,
2 way:
Separately calculating the volumes of top and bottom of prisms and adding to get the volume of the composed figure.
Check Understanding Math Board
Find the volume of the composed figure.
Question 1.
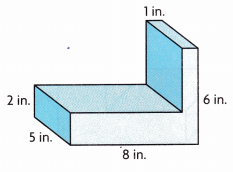
________
Answer:
Volume of composed figure is 100 cubic in,
Explanation:
Given to find the volume of composed figure,
we separately calculate volumes of top and bottom of prisms then add so base rectangular prism has length 8 in,
width 5 in and height 2 in, volume of bottom prism is
8 in X 5 in X 2 in = 80 cubic in, the top prism dimensions are length 1 in, width 5 in and height 4 in(6 in – 2 in), volume of top prism is
1 in X 5 in X 4 in = 20 cubic in, Now the volume of composed figure is 80 cubic in + 20 cubic in = 100 cubic in.
Question 2.
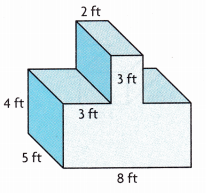
________
Answer:
Volume of composed figure is 190 cubic ft,
Explanation:
Given to find the volume of composed figure,
we separately calculate volumes of top and bottom of prisms then add so base rectangular prism has length 8 ft,
width 5 ft and height 4 ft, volume of bottom prism is
8 ft X 5 ft X 4 ft = 160 cubic ft, the top prism dimensions are length 2 ft, width 5 ft and height 3 ft, volume of top prism is
2 ft X 5 ft X 3 ft = 30 cubic ft, Now the volume of composed figure is 160 cubic ft + 30 cubic ft = 190 cubic ft.
On Your Own
Question 3.
Use Structure Carlo is making a fabric chair filled with foam using the design shown. He wants to find the amount of foam he needs to make the chair.
- Describe how to find the volume of the chair by breaking apart the figure into right rectangular prisms.
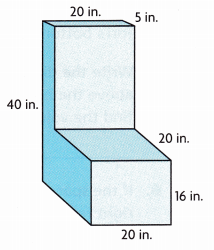
- Describe how to find the volume of the chair using subtraction.
- How much foam does Carlo need? ______
Answer:
Volume of the chair by breaking apart is 8,800 cubic in,
Volume of the chair using subtraction is 8,800 cubic in,
Carlo needs 8,800 cubic in of foam,
Explanation:
Given Carlo is making a fabric chair filled with foam using the design shown
1. The volume of the chair by breaking apart the figure into right rectangular prisms as top and bottom bottom prism dimensions length is 20 in, width 20 in and height 16 in , volume of bottom prism is
20 in X 20 in X 16 in = 6,400 cubic in,
Top prism dimensions are length 20 in, width 5 in and height is 24 in( 40 in – 16 in), volume of top prism is
20 in X 5 in X 24 in = 2,400 cubic in,
Total volume of the chair by breaking apart is
6,400 cubic in + 2,400 cubic in = 8,800 cubic in,
2. Volume of the chair using subtraction is
Volume of total chair with space minus
volume of the space, Dimensions of total chair is length 20 in, width 20 in and height is 40 in,
volume = 20 in X 20 in X 40 in = 16,000 cubic in,
Volume of space dimensions are length 20 in, width 15 in and height is 24 in (40 in – 16 in),
Volume = 20 in X 15 in X 24 in = 7,200 cubic in,
Volume of chair is 16,000 cubic in – 7,200 cubic in = 8,800 cubic in,
3. Carlo needs 8,800 cubic in. of foam.
Find the volume of the composed figure.
Question 4.
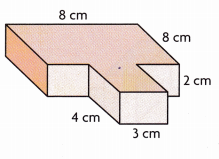
________
Answer:
Volume of composed figure is 152 cubic cm,
Explanation:
Given to find the volume of composed figure, we separately calculate volumes of base 1 of prisms and extended base then add so base 1 rectangular prism has length 8 cm, width 8 cm and height 2 cm, volume of base 1 prism is 8 cm X 8 cm X 2 cm = 128 cubic cm, the extended base prism dimensions are length 3 cm, width 4 cm and height 2 cm, volume of extended base prism is 3 cm X 4 cm X 2 cm = 24 cubic cm, Now the volume of composed figure is 128 cubic cm + 24 cubic cm = 152 cubic cm.
Question 5.
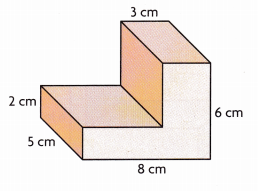
________
Answer:
Volume of composed figure is 140 cubic cm,
Explanation:
Given to find the volume of composed figure,
we separately calculate volumes of top and bottom of prisms then add so base rectangular prism has length 8 cm,
width 5 cm and height 2 cm, volume of bottom prism is 8 cm X 5 cm X 2 cm = 80 cubic cm, the top prism dimensions are length 3 cm, width 5 cm and height 4 cm(6 cm – 2 cm), volume of top prism is 3 cm X 5 cm X 4 cm = 60 cubic cm, Now the volume of composed figure is 80 cubic cm + 60 cubic cm = 140 cubic cm.
Question 6.
Reason The volume of the composed figure shown is 88 cubic inches. What is the unknown number? Explain how you know.
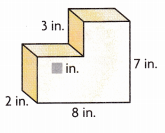
Answer:
Unknown number is 4 in,
Explanation:
Given the volume of the composed figure shown is 88 cubic inches. Asking the unknown number?
we separately calculate volumes of top and bottom of prisms then add so base rectangular prism has length 8 in,
width 2 in and height 4 in(7in – 3 in), volume of bottom prism is
8 in X 2 in X 4 in = 64 cubic in,
we will have unknow space length as x the top prism dimensions are length (8 in – x in), width 2 in and height 7 in, volume of top prism is
(8 in – x in) X 2 in X 3 in = (8 in – x in) x 6 square in,
Given the volume of composed figure as 88 cubic in,
so 64 cubic in + (8 in – x in) x 6 square in = 88 cubic in,
(8 in – x in) x 6 square in = 88 cubic in – 64 cubic in = 24 cubic in,
(8 in – x in) = 24 cubic in ÷ 6 square in = 4 in,
So x in = 8 in – 4 in = 4 in.
therefore unknown number is 4 in.
Find the volume of the composed figure.
Question 7.
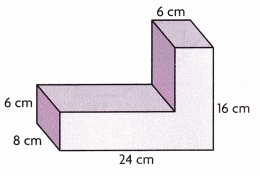
______
Answer:
Volume of composed figure is 1,632 cubic cm,
Explanation:
Given to find the volume of composed figure,
we separately calculate volumes of top and bottom of prisms then add so base rectangular prism has length 24 cm,
width 8 cm and height 6 cm,
volume of bottom prism is 24 cm X 8 cm X 6 cm =
1,152 cubic cm, the top prism dimensions are
length 6 cm, width 8 cm and height 10 cm(16 cm – 6 cm),
volume of top prism is 6 cm X 8 cm X 10 cm = 480 cubic cm,
Now the volume of composed figure is
1,152 cubic cm + 480 cubic cm = 1,632 cubic cm.
Question 8.
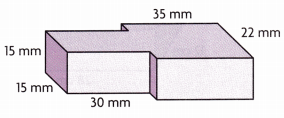
________
Answer:
Volume of composed figure is 18,300 cubic mm,
Explanation:
Given to find the volume of composed figure,
we separately calculate volumes of base 1 of prisms and extended base then add so base 1 rectangular prism has length 35 mm, width 22 mm and height 15 mm, volume of base 1 prism is
35 mm X 22 mm X 15 mm = 11,550 cubic mm, the extended base prism dimensions are
length 30 mm, width 15 mm and height 15 mm, volume of extended base prism is
30 mm X 15 mm X 15 mm = 6,750 cubic mm,
Now the volume of composed figure is 11,550 cubic mm + 6,750 cubic mm = 18,300 cubic mm.
Question 9.
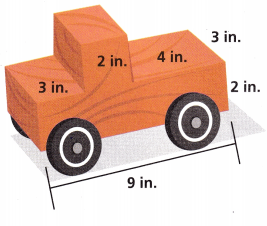
______
Answer:
Volume of composed figure is 66 cubic in,
Explanation:
Given to find the volume of composed figure,
we separately calculate volumes of top and bottom of prisms then add so base rectangular prism has length 9 in,
width 3 in and height 2 in, volume of bottom prism is 9 in X 3 in X 2 in = 54 cubic in, the top prism dimensions are length 2 in, width 3 in and height 2 in, volume of top prism is 2 in X 3 in X 2 in = 12 cubic in, Now the volume of composed figure is 54 cubic in + 12 cubic in = 66 cubic in.
Question 10.
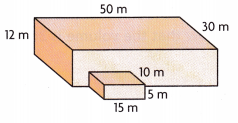
______
Answer:
Volume of composed figure is 18,750 cubic m,
Explanation:
Given to find the volume of composed figure,
we separately calculate volumes of base 1 of prisms and
extended base then add so base 1 rectangular prism
has length 50 m, width 30 m and height 12 m,
volume of base 1 prism is
50 m X 30 m X 12 m = 18,000 cubic m,
the extended base prism dimensions are
length 15 m, width 10 m and height 5 m,
volume of extended base prism is
15 m X 10 m X 5 m = 750 cubic m,
Now the volume of composed figure is
18,000 cubic m + 750 cubic m = 18,750 cubic m.
On Your Own
Question 11.
Model with Mathematics Write an addition expression to model the volume of the solid figure.
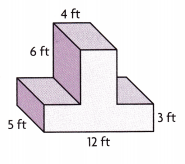
Answer:
Addition expression to model the volume of the
solid figure is 180 cubic ft + 120 cubic ft = 300 cubic ft,
Explanation:
Given to find the volume of composed figure,
we separately calculate volumes of top and bottom of prisms
then add so base rectangular prism has length 12 ft,
width 5 ft and height 3 ft, volume of bottom prism is
12 ft X 5 ft X 3 ft = 180 cubic ft, the top prism dimensions
are length 4 ft, width 5 ft and height 6 ft,
volume of top prism is 4 ft X 5 ft X 6 ft = 120 cubic ft,
Addition expression to model the volume of the
solid figure is 180 cubic ft + 120 cubic ft = 300 cubic ft.
Write the unknown dimensions, and then find the volume of the composed figure.
Question 12.
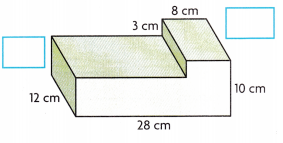
_________
Answer:
Volume of composed figure is 2,640 cubic cm,
Explanation:
Wrote the unknown dimensions as height of
bottom prism as 7 cm and width of top prism as 12 cm,
Given to find the volume of composed figure,
we separately calculate volumes of top and bottom of prisms
then add so base rectangular prism has length 28 cm,
width 12 cm and height 7 cm(10 cm – 3 cm),
volume of bottom prism is 28 cm X 12 cm X 7 cm =
2,352 cubic cm, the top prism dimensions are
length 8 cm, width 12 cm and height 3cm,
volume of top prism is 12 cm X 8 cm X 3 cm = 288 cubic cm,
Now the volume of composed figure is
2,352 cubic cm + 288 cubic cm = 2,640 cubic cm.
Question 13.
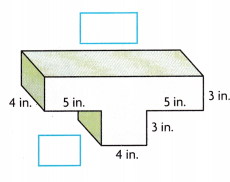
_________
Answer:
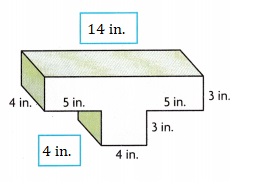
Volume of composed figure is 216 cubic in,
Explanation:
Wrote the unknown dimensions as width of
bottom prism as 4 in and length of top prism as 14 in,
Given to find the volume of composed figure,
we separately calculate volumes of top and bottom of prisms
then add so base rectangular prism has length 4 in,
width 4 in and height 3 in, volume of bottom prism is
4 in X 4 in X 3 in = 48 cubic in, the top
prism dimensions are length 14 in, width 4 in
and height 3 in, volume of top prism is
14 in X 4 in X 3 in = 168 cubic in, Now the volume of
composed figure is 48 cubic in + 168 cubic in = 216 cubic in.
Question 14.
Open Ended Draw a composed figure with a volume of 36 cubic feet. Label the measurements of the figure, and show that the volume is 36 cubic feet.
Answer:
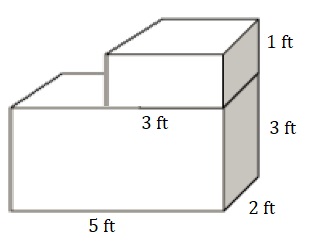
Shown the volume of composed figure as 36 cubic feet,
Explanation:
Drawn a composed figure with a volume of 36 cubic feet.
Labeled the measurements of the figure and
shown that the volume as 36 cubic feet.
We separately calculate volumes of top and bottom of prisms
then add so base rectangular prism has length 5 ft,
width 2 ft and height 3 ft, volume of bottom prism is
5 ft X 2 ft X 3 ft = 30 cubic ft, the top
prism dimensions are length 3 ft, width 2 ft
and height 1 ft, volume of top prism is
3 ft X 2 ft X 1 ft = 6 cubic ft, Now the volume of
composed figure is 30 cubic ft + 6 cubic ft = 36 cubic ft.
Question 15.
Model with Mathematics Write a subtraction expression to model the volume of the solid figure.
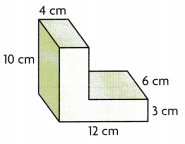
Answer:
Subtraction expression to model the volume of
the solid figure is 384 cubic cm.
Explanation:
Writing a subtraction expression to model the
volume of the solid figure first we calculate
the volume of rectangular prism with space then
subtract volume of space, So the volume of
rectangular prism with space as length 12 cm,
width 6 cm and height 10 cm is
12 cm X 6 cm X 10 cm = 720 cubic cm,
Volume of the space is length = 12 cm – 4 cm = 8 cm,
width = 6 cm and height = 10 cm – 3 cm = 7 cm,
so 8 cm X 6 cm X 7 cm = 336 cubic cm,
Now subtraction expression to model the volume of
the solid figure is 720 cubic cm – 336 cubic cm = 384 cubic cm.