We included HMH Into Math Grade 5 Answer Key PDF Module 5 Lesson 5 Apply Volume Formulas to make students experts in learning maths.
HMH Into Math Grade 5 Module 5 Lesson 5 Answer Key Apply Volume Formulas
I Can use a formula to find the volume of a right rectangular prism.
Step It Out
1. Jeanie buys the fish tank shown.
A. You know that the volume of a rectangular prism can be expressed as the product of its length, width, and height. Write a formula to model the volume of a rectangular prism.
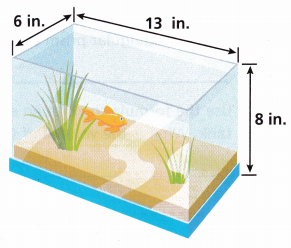
B. Use the formula to write an equation for the volume of the tank.
C. Multiply from left to right. What is the product of the length and width?
D. Multiply the product of the length and width by the height. What is the volume of the fish tank?
Answer:
A. Volume of a rectangular prism = length X width X height,
B. Volume of tank = 13 in X 6 in X 8 in,
C. Product of the length and width is 13 X 6 = 78 sq in,
D. Volume of tank 624 cubic in,
Explanation:
Given Jeanie buys the fish tank shown.
A. I know that the volume of a rectangular prism can be expressed as the product of its length, width, and height. The formula to model the volume of a rectangular prism is length X width X height,
B. As length of tank is 13 in, width is 6 in and height is 8 in, so volume of tank = 13 in X 6 in X 8 in,
C. Multiplying from left to right the product of the length and width is13 X 6 = 78 sq in,
D. Multiplying the product of the length and width by the height. The volume of the fish tank is 78 sq in X 8 in = 624 cubic in.
Turn and Talk How can you use the Associative Property of Multiplication to identify the part of the formula that represents the area of the base of the rectangular prism?
Answer:
The first part of the associative property of multiplication can be represented to the area of the base of the rectangular prism,
Explanation:
The associative property is a math rule that says that the way in which factors are grouped in a multiplication problem does not change the product. So the first part of the associative property of multiplication can be represented to the area of the base of the rectangular prism.
2. Jeanie finds another fish tank in the shape of a right rectangular prism with the dimensions shown.
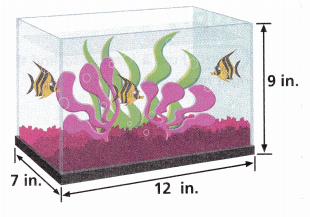
A. Let B represent the base area of a right rectangular prism. What equation represents the base area of the fish tank?
B. Write a formula to model the volume of a right rectangular prism using B.
C. Use the formula to write an equation for the volume of the tank. What is the volume of the tank?
Answer:
A. B = 12 in X 7 in,
B. Volume V = B X height,
C. V = 12 in X 7 in X 9 in,
Volume of the tank is 756 cubic inches.
Explanation:
Given Jeanie finds another fish tank in the shape of a right rectangular prism with the dimensions as length 12 in, width 7 in and height 9 in,
A. If B represent the base area of a right rectangular prism. The equation represents the base area of the fish tank is
B = 12 in X 7 in,
B. The formula to model the volume of a right rectangular prism using B is V = B X height.
C. Using the formula to write an equation for
the volume of the tank is V = 12 in X 7 in X 9 in,
the volume of the tank is 756 cubic inches.
Check Understanding Math Board
Question 1.
A storage unit is 12 feet wide, 8 feet long, and 9 feet high. What is the volume of the storage unit? _____
Answer
Volume of storage unit is 864 cubic feet,
Explanation:
Given a storage unit is 12 feet wide, 8 feet long, and
9 feet high. So the volume of the storage unit is
V = 8 feet X 12 feet X 9 feet = 864 cubic feet.
On Your Own
Question 2.
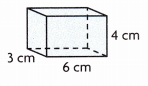
V = ___
Answer:
Volume = 72 cubic cms.
Explanation:
Given length 6 cm, width 3 cm and height 4 cm
so volume = 6 cm X 3 cm X 4 cm = 72 cubic cms.
Question 3.
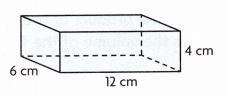
V = ___
Answer:
Volume = 288 cubic cms.
Explanation:
Given length 12 cm, width 6 cm and height 4 cm
so volume = 12 cm X 6 cm X 4 cm = 288 cubic cms.
Question 4.
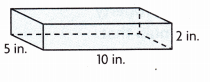
V = ___
Answer:
Volume = 100 cubic in.
Explanation:
Given length 10 in, width 5 in and height 2 in
so volume = 10 in X 5 in X 2 in = 100 cubic in.
Question 5.
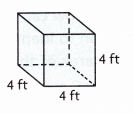
V = ___
Answer:
Volume = 64 cubic ft.
Explanation:
Given length 4 ft, width 4 ft and height 4 ft
so volume = 4 ft X 4 ft X 4 ft = 64 cubic ft.
On Your Own
Question 6.
Zachary has a trunk with the dimensions shown. What is the volume of the trunk?

Answer:
Volume of trunk is 6,240 cubic in,
Explanation:
Given Zachary has a trunk with the dimensions
length 30 in, width 16 in and height 13 in,
so volume of the trunk is 30 in X 16 in X 13 in = 6,240 cubic in.
Question 7.
Use Structure A dresser is in the shape of a right rectangular prism. The area of the base is 6 square feet and the height is 4 feet. What is the volume of the dresser?
Answer:
The volume of the dresser is 24 cubic feet,
Explanation:
Given a dresser is in the shape of a right rectangular prism.
The area of the base is 6 square feet and the height is 4 feet.
So the volume of the dresser is area of the base X height,
V = 6 sq feet X 4 feet = 24 cubic feet.
Find the volume.
Question 8.
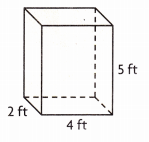
V = ___
Answer:
Volume = 40 cubic ft.
Explanation:
Given length 4 ft, width 2 ft and height 5 ft
so volume = 4 ft X 2 ft X 5 ft = 40 cubic ft.
Question 9.
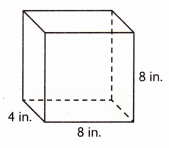
V = ___
Answer:
Volume = 256 cubic in.
Explanation:
Given length 8 in, width 4 in and height 8 in
so volume = 8 in X 4 in X 8 in = 256 cubic in.
Question 10.
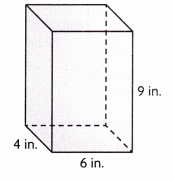
V = ___
Answer:
Volume = 216 cubic in.
Explanation:
Given length 6 in, width 4 in and height 9 in
so volume = 6 in X 4 in X 9 in = 216 cubic in.
Question 11.
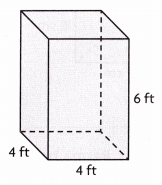
V = ___
Answer:
Volume = 96 cubic ft.
Explanation:
Given length 4 ft, width 4 ft and height 6 ft
so volume = 4 ft X 4 ft X 6 ft = 96 cubic ft.
Question 12.
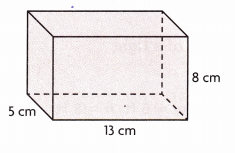
V = ___
Answer:
Volume = 520 cubic cms.
Explanation:
Given length 13 cm, width 5 cm and height 8 cm
so volume = 13 cm X 5 cm X 8 cm = 520 cubic cms.
Question 13.
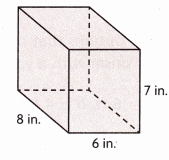
V = ___
Answer:
Volume = 336 cubic in.
Explanation:
Given length 6 in, width 8 in and height 7 in
so volume = 6 in X 8 in X 7 in = 336 cubic in.
On Your Own
Question 14.
Attend to Precision Jason has gift boxes with the same dimensions as the one shown. He fits all of his boxes exactly into a larger box with a volume of 1,152 cubic inches. How many gift boxes are in the larger box? Explain how you know.
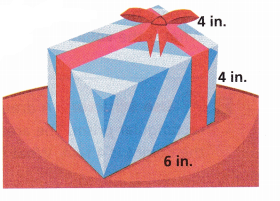
Answer:
Number of gift boxes in the larger box are 12,
Explanation:
Given Jason has gift boxes with the same dimensions as the one shown.
Length 6 in, width 4 in and height 4 in,
He fits all of his boxes exactly into a larger box with a volume of 1,152 cubic inches.
N Number of gift boxes are in the larger box are as we know N = volume of larger box ÷ volume of gift box,
so N = 1,152 ÷ (6 in X 4 in X 4 in) = 1,152 ÷ 96 = 12.
therefore number of gift boxes in the larger box are 12.
Question 15.
Reason A closet is in the shape of a right rectangular prism. The area of the floor is 9 The volume of the closet is 72 cubic feet. What is height of the closet? ______
Answer:
Height of closet is 8 feet,
Explanation:
Given a closet is in the shape of a right rectangular prism. The area of the floor is 9 square feet,
The volume of the closet is 72 cubic feet.
so height of the closet is as V = area of closet X height,
height = volume of closet ÷ area of closet,
height = 72 cubic feet ÷ 9 square feet = 8 feet
Find Volume of Composed Figures
Question 16.
V = 168 cu cm
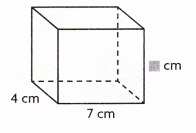
Answer:
Height is 6 cm,
Explanation:
Given length 7 cm, width 4 cm and height be h and volume 168 cu cm so height is
168 cu cm = 7 cm X 4 cm X h,
h = 168 cu cm ÷ (7 cm X 4 cm) =
168 cu cm ÷ 28 sq cm = 6 cm,
therefore height is 6 cm.
Question 17.
V = 360 cu in
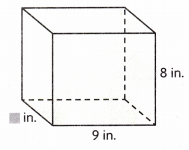
Answer:
width is 5 in,
Explanation:
Given length 9 in, width w and height is 8 in
and volume 360 cu in so height is
360 cu cm = 9 in X w X 8 in,
w = 360 cu in ÷ (9 in X 8 in) =
360 cu in ÷ 72 sq cm = 5 in,
therefore width is 5 in.
Question 18.
Reason Parma has a box that is in the shape of a right rectangular prism. The length of the box is twice the height. The length is 6 inches longer than the width. If the height is 8 inches, what is the volume of the box? ________
Answer:
The volume of the box is 1,280 cubic inches,
Explanation:
Given Parma has a box that is in the shape of a right rectangular prism. The length of the box is twice the height. The length is 6 inches longer than the width. If the height is 8 inches then length is
2 X 8 inches = 16 inches, width is 16 inches – 6 inches = 10 inches so the volume is 16 inches X 10 inches X 8 inches,
V = 1,280 cubic inches.
Question 19.
Circle all the options that could be the dimensions of a right rectangular prism with a volume of 192 cubic feet.
l = 8 ft, w = 6 ft, h = 4 ft l = 6 ft, w = 6 ft, h = 8 ft
l = 8 ft, w = 3ft, h = 8ft l = 4 ft, w = 3 ft, h = 16ft
l = 5 ft, w = 4 ft, h = 12ft l = 10 ft, w = 6 ft, h = 4 ft
Answer:
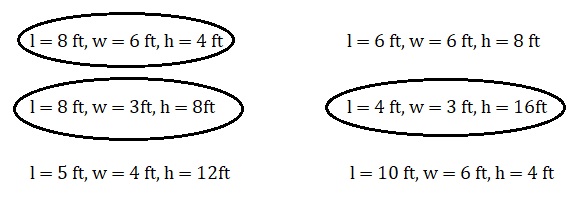
Explanation:
Given to circle all the options that could be the dimensions of a right rectangular prism with a volume of 192 cubic feet are
1. l = 8 ft, w = 6 ft, h = 4 ft,
V= 8 ft X 6 Ft X 4 ft = 192 cubic ft,
2. l = 6 ft, w = 6 ft, h = 8 ft,
V = 6 ft X 6 ft X 8 ft = 288 cubic ft,
3. l = 8 ft, w = 3ft, h = 8ft,
V = 8 ft X 3 ft X 8 ft = 192 cubic ft,
4. l = 4 ft, w = 3 ft, h = 16ft,
V = 4 ft X 3 ft X 16 ft = 192 cubic ft,
5. l = 5 ft, w = 4 ft, h = 12ft
V = 5 ft X 4 ft X 12 ft = 240 cubic ft,
6. l = 10 ft, w = 6 ft, h = 4 ft
V =10 ft X 6 ft X 12 ft = 720 cubic ft
So circled l = 8 ft, w = 6 ft, h = 4 ft,
l = 8 ft, w = 3ft, h = 8ft and l = 4 ft, w = 3 ft, h = 16ft
whose volume is of 192 cubic feet as shown above.