We included HMH Into Math Grade 5 Answer Key PDF Module 10 Understand Division with Whole Numbers and Unit Fractions to make students experts in learning maths.
HMH Into Math Grade 5 Module 10 Answer Key Understand Division with Whole Numbers and Unit Fractions

Astrophysicist
Astrophysicists use mathematics to explain their theories about the life cycles of galaxies, stars, and planets. Stephen Hawking was one of the world’s most renowned astrophysicists.
Astrophysicists at NASA try to answer: How does the universe work? How did we get here? Are we alone? Astrophysicists analyze data and develop models. They have to persevere when they get stuck trying to make a good model.
Since 300 BC, astrophysicists have observed how the sun and stars move. They used this data to model our solar system. The first models did not explain all the data, so they persevered until the 1600s, when they made a model that worked.
STEM Task:
Galileo observed that Venus has phases and used this data to support the model of the solar system. Like Venus, our moon has phases. Research the phases of the moon and select one to focus on. What fraction of a month is this phase visible? Share your data with a partner. Write one question an astrophysicist might ask about the solar system based on this data.
Answer:
Eight phases of moon,
In which phase does solar eclipses occur?
Explanation:
The eight phases of the Moon in order are:
- new Moon
- waxing crescent Moon
- first quarter Moon
- waxing gibbous Moon
- full Moon
- waning gibbous Moon
- last quarter Moon
waning crescent Moon.
New moon occurs when the moon is on the same side of Earth as the sun.
New moons generally can’t be seen.
They cross the sky with the sun during the day and the moon’s shadow side is pointed toward Earth.
Question an astrophysicist might ask about the solar system based on this data is
In which phase does solar eclipses occur?.
Learning Mindset Perseverance Getting Unstuck

Solving problems takes time. It often requires trying different strategies. Sometimes a small, unseen error can get you stuck. Slow down. Work the problem backwards. Check your work. There are times you might need help getting unstuck, so one of your strategies might be to ask for help. But don’t give up too soon! Mathematicians and scientists sometimes take years to solve problems. One man took 14 years to find a prime number that has over 23 million digits!
Reflect
Question 1.
Think about a time you were working on a math problem and you got stuck. Was your strategy wrong or did you make an error executing the strategy? How did you get unstuck?
Answer:
Error executing the startegy,
Explanation:
Thinking about a time I was working on a math problem and I got stuck. Made an error executing the strategy,
I get unstuck by finding error and again executing the with error free.
Question 2.
In the STEM Task, were your research strategies effective?
Answer:
Yes, research strategies are effective,
What is the secret number?
Follow the steps to find the number of words in the Constitution of the United States of America, including all 27 amendments.
A. Complete each equation to represent the shaded part of each fraction strip.
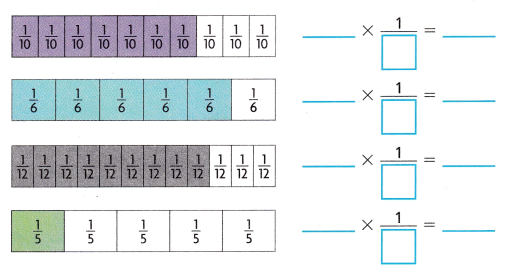
Answer:
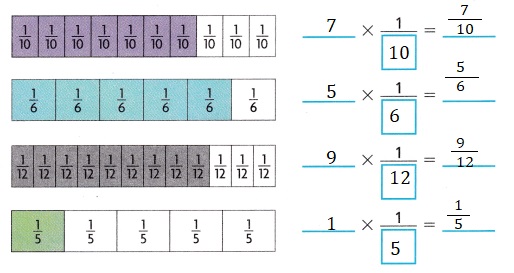
Explanation:
Completed each equation to represent the shaded part of each fraction strip as shown above.
B. Write a 4-digit number using the whole-number factors from each equation. Write the factors in the same order as they appear.
The Constitution has _____ words.
Answer:
4,440 words
Turn and Talk
Describe how to find the product 3 × \(\frac{1}{8}\) without using a picture or repeated addition.
Answer:
\(\frac{3}{24}\),
Explanation:
The product 3 × \(\frac{1}{8}\) without using a picture or repeated addition is by seeing only we can say 3 multiplied by \(\frac{1}{8}\) is \(\frac{3 X 1}{3 X 8}\) =
\(\frac{3}{24}\),
Are You Ready?
Complete these problems to review prior concepts and skills you will need for this module.
Represent Division
Complete the table. Use counters to help.
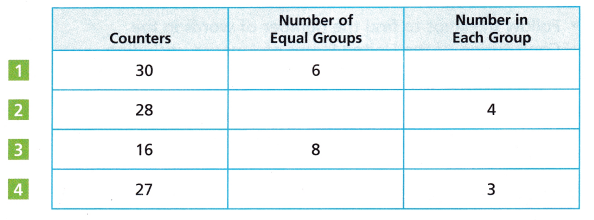
Answer:
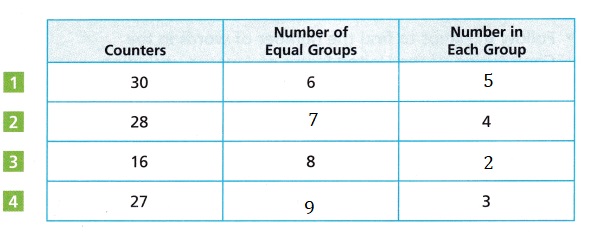
Explanation:
Used counters to complete the data as
1. 30 ÷ 6 = 5,
2. 28 ÷ 4 = 7,
3. 16 ÷ 8 = 2,
4. 27 ÷ 3 = 9,
shown above.
Relate Multiplication and Division
Write the related facts for each set.
Question 5.
6, 7, 42
___________ ÷ ___________ = ___________
___________ × ___________ = ___________
___________ ÷ ___________ = ___________
___________ × ___________ = ___________
Answer:
42 ÷ 6 = 7,
6 X 7 = 42,
42 ÷ 7 = 6,
7 X 6 = 42,
Explanation:
Given set is 6, 7, 42 the related facts are
when 42 is divided by 6 we get 42 ÷ 6 = 7,
when 6 multiplied by 7 we will get 6 X 7 = 42,
when 42 is divided by 7 we get 42 ÷ 7 = 6,
when 7 multiplied by 6 we will get 7 X 6 = 42.
Question 6.
3, 8, 24
___________ ÷ ___________ = ___________
___________ × ___________ = ___________
___________ ÷ ___________ = ___________
___________ × ___________ = ___________
Answer:
24 ÷ 3 = 8,
3 X 8 = 24,
24 ÷ 8 = 3,
8 X 3 = 24,
Explanation:
Given set is 3, 8, 24 the related facts are
when 24 is divided by 3 we get 24 ÷ 3 = 8,
when 3 multiplied by 8 we will get 3 X 8 = 24,
when 24 is divided by 8 we get 24 ÷ 8 = 3,
when 8 multiplied by 3 we will get 8 X 3 = 24.
Question 7.
2, 9, 18
___________ ÷ ___________ = ___________
___________ × ___________ = ___________
___________ ÷ ___________ = ___________
___________ × ___________ = ___________
Answer:
18 ÷ 2 = 9,
2 X 9 = 18,
18 ÷ 9 = 2,
9 X 2 = 18,
Explanation:
Given set is 2, 9, 18 the related facts are
when 18 is divided by 2 we get 18 ÷ 2 = 9,
when 2 multiplied by 9 we will get 2 X 9 = 18,
when 18 is divided by 9 we get 18 ÷ 2 = 2,
when 9 multiplied by 2 we will get 9 X 2 = 18.
Equivalent Fractions
Write an equivalent fraction.
Question 8.
\(\frac{16}{48}\) = ____________
Answer:
\(\frac{4}{12}\) or \(\frac{1}{3}\),
Explanation:
Given \(\frac{16}{48}\) as numerator and denominator goes in 4, so \(\frac{4 X 4}{4 X 12}\),
as 4 goes it is \(\frac{4}{12}\) and again it can be further divided by 4 as \(\frac{4 X 1}{4 X 3}\) we get
\(\frac{1}{3}\), So the equivalent fraction for
\(\frac{16}{48}\) = \(\frac{4}{12}\) or \(\frac{1}{3}\).
Question 9.
\(\frac{6}{7}\) = ____________
Answer:
\(\frac{12}{14}\),
Explanation:
Given \(\frac{6}{7}\) as numerator and denominator does donot have any common factors, to get equivalent fraction we multiply numerator and denominator by any one common number from 2, here we take 2 so \(\frac{2 X 6}{2 X 7}\) = \(\frac{12}{14}\).
Question 10.
\(\frac{5}{13}\) = ____________
Answer:
\(\frac{15}{39}\),
Explanation:
Given \(\frac{5}{13}\) as numerator and denominator does donot have any common factors, to get equivalent fraction we multiply numerator and denominator by any one common number from 2, here we take 3 so \(\frac{3 X 6}{3 X 7}\) = \(\frac{15}{39}\).
Question 11.
\(\frac{16}{32}\) = ____________
Answer:
\(\frac{4}{8}\) or \(\frac{1}{2}\),
Explanation:
Given \(\frac{16}{32}\) as numerator and denominator goes in 4, so \(\frac{4 X 4}{4 X 8}\),
as 4 goes it is \(\frac{4}{8}\) and again it can be further divided by 4 as \(\frac{4 X 1}{4 X 2}\) we get
\(\frac{1}{2}\), So the equivalent fraction for
\(\frac{16}{32}\) = \(\frac{4}{8}\) or \(\frac{1}{2}\).
Question 12.
\(\frac{14}{18}\) = ____________
Answer:
\(\frac{7}{9}\)
Explanation:
Given \(\frac{14}{18}\) as numerator and denominator goes in 2, so \(\frac{2 X 7}{2 X 9}\), as 2 goes it is \(\frac{14}{18}\), So the equivalent fraction for \(\frac{14}{18}\) = \(\frac{7}{9}\).
Question 13.
\(\frac{55}{66}\) = ____________
Answer:
\(\frac{5}{6}\),
Explanation:
Given \(\frac{55}{66}\) as numerator
and denominator goes in 11, so \(\frac{11 X 5}{11 X 6}\),
as 6 goes it is \(\frac{5}{6}\), So the equivalent fraction for
\(\frac{55}{66}\) = \(\frac{5}{6}\).