The Students who believe learning the Highest Common Factors concept is difficult and confusing, will no longer feel HCF. The Highest Common Factor for two or more natural numbers is known as HCF. For better understanding, we have provided various questions with a brief explanation. Practice the problems given on Highest Common Factor (HCF) on this page and enhance your math skills.
Know how questions are framed on the topic of HCF by referring to the Word Problems on HCF and get an idea of how to find HCF quickly using various methods. We will show different methods to solve the problems on Highest Common Factor (HCF).
Do Refer:
Highest Common Factor (H.C.F) – Definition
The largest common factor of all the given numbers is called as Highest Common Factor (H. C. F). The number can be divided into exactly two or more numbers without any remainder. The HCF is also known as the Greater Common Factor (GCF). The easiest way to find the HCF of two given numbers is to create a Tree factor. Let us discuss with an example about HCF.
Example: Find the HCF of 2 and 4
Solution:
Factors of 2 are 2 x 1
Factors of 4 are 2 x 2
Thus the Highest Common Factors of 2 and 4 are 2.
H.C.F Formula
H.C.F is simply the Highest Common Factor. Let a and b be two integers. The formula to find the HCF of a and b is given as,
HCF = Product of two numbers / L.C.M of two numbers
HCF = (a x b) / L.C.M (a,b)
Where L.C.M is the Least Common Multiple.
How to Find HCF (Highest Common Factor)?
There are three methods to find the Highest Common Factor of two or more numbers. The three methods to find the HCF of the integers is as follows,
1. Prime Factorization Method (Factor Tree Method)
2. Division Method
3. Factorization Method
These three different methods are to find the H.C.F of given numbers is explained step by step here.
1. HCF by Prime Factorization (Factor Tree Method):
In calculating HCF by Prime Factorization, we factorize the numbers into Prime factors, which is known as Prime Factors. Follow the below steps to find the HCF of numbers using the Prime Factorization Method,
Step 1: Initially, check whether the given number is divisible by 2.
Step 2: Now, divide until you cannot divide the number any further.
Step 3: Finally, write the numbers as the product of the prime numbers. The product of those common factors is that the Highest Factor of the given numbers.
Example: What is the HCF of 6 and 8?
Solution: The values are 6 and 8.
Factors of 6 are,
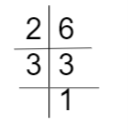
2 x 3 = 6
Factors of 8 are,
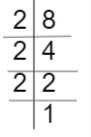
2 x 2 x 2 = 8
The Common Factor is 2.
Thus, the HCF of 6 and 8 is 2.
2. HCF by Division Method:
You have understood by now the strategy of finding the common highest factor using Prime Factorization. Now, learn here to find HCF using Division Method. The division method is nothing but divides the given number, simultaneously, to get the common factors between them. Follow the steps mentioned below of division method,
Step 1: In the division method, first, treat the smaller number as the divisor and the bigger number as the dividend.
Step 2: Divide the given number until you get the remainder as 0.
Step 3: We are going to get the common prime factors because the factors within the left-hand side divide all the numbers exactly. The product of those common prime factors is that the HCF of the given numbers.
Example: Find the HCF of the 10 and 15?
Solution: Given the values 10 and 15,
Using the division method,
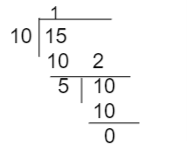
Thus, the HCF of given numbers 10 and 15 is 5.
3. HCF by Factorization Method:
In HCF by finding the Factorization Method, we will find the greatest common factor by listing down the factors of the numbers. Follow the below steps for finding the HCF using the Factorization method,
Step 1: First, Write the factors of the given numbers.
Step 2: Next, find the highest factor among the listed factors which are common for both the given numbers.
Example: What’s the HCF of 12 and 24?
Solution: Given the values are 12 and 24.
The Factors of 12 are 1, 2, 3, 4, 6
The Factors of 24 are 1, 2, 3, 4, 6
So, the common factors of given numbers are 1, 2, 3, 6.
The Highest factor among them is 6.
Thus, the HCF of given numbers 12 and 24 is 6.
Practice Math Online with Unlimited Questions provided in 5th Grade Math Activity Sheets and become a blossoming mathematician in no time.
Properties of HCF
The Properties of HCF are listed in the below lines for quick reference. They are as under
Property 1: The HCF of any two or more numbers isn’t greater than any of the given numbers.
Property 2: If one number is the factor of the other number, their HCF will be the smallest number.
Property 3: The HCF of the numbers is the product of the co-prime factors.
Property 4: HCF of two or more Prime numbers is always 1.
Highest Common Factor Examples
Example 1:
Find the H.C.F of three numbers 27, 21, 24 by Prime Factorization Method?
Solution:
Given the values are 27, 21, 24
Now, first, we have to write the factors of the given three numbers.
The factors of 27 are 1, 3, 9, and 27.
The factors of 21 are 1, 3, 7.
Factors of 24 are 1, 2, 3, 4, 6, 8,12.
Now, we have to write the common factors of all the three given numbers.
Common Factors of 24, 21, 27 = 1, 3
So, the HCF of three numbers 24, 21, 27 is 3.
Example 2:
Find the HCF of three numbers are 25, 30, 35?
Solution:
As given the question, the values are 25, 30, and 35.
We can find the HCF of 25, 30, and 35 using the Factorization method.
The factors of 25 are 5 x 5.
The factors of 30 are 5 x 6.
The factors of 35 are 5 x 7.
The common factors of 25, 30, and 35 are 5, 6, 7.
Therefore, the highest common factor of given numbers is 5.
Example 3:
What is the HCF of 48 and 56 using the Prime Factorization Method?
Solution:
Given the values 48 and 56.
Now, we find the HCF using the Prime Factorization Method.
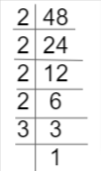
So, the factors of 48 is 2 x 2 x 2 x 2 x 3
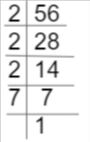
Now, the Factors of 56 = 2 x 2 x 2 x 7
The Highest Common Factors (H.C.F) of given numbers are 2 x 2 x 2.
Hence, the HCF of 48 and 56 is 2 x 2 x 2 = 8.
Example 4:
What is the HCF 9, 75 using the Division Method?
Solution:
Given the values are 9 and 75.
Now, using the division method find the HCF value.
First, divide 9 and 75. If the remainder will become the new divisor then 9 will become the new dividend.
Next, proceed with this process till the remainder is zero and therefore the last divisor is going to be the HCF of the given number.
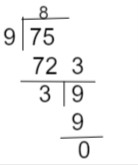
Thus, the HCF of 9 and 75 is 3.
Example 5:
Write the Highest Common Factor (H.C.F) of 16 and 20?
Solution:
Given the values 16 and 20.
Now, find the factors
The Factors of 16 are 1, 2, 4, 8.
The factors of 20 are 1, 2, 4, 5.
Therefore the common factors of 16 and 20 are 1, 2, 4
The Highest Common Factor (H.C.F) among them is 4.
Therefore, 4 is the H.C.F or G.C.D of given numbers.
FAQ’s on Highest Common Factor (H.C.F)
1. How do find HCF?
For finding the HCF of two or more numbers, we have three methods. The methods are,
1. Division Method
2. Factorization Method
3. Prime Factorization Method
2. Write the relation between HCF and LCM?
LCM and HCF are related by the formula:
LCM (a, b) = a × b/HCF(a,b)
Where a and b are two different numbers.
3. What’s Highest Common Factor?
It is the Highest of the common factor of two or more numbers.
4. How do we use Highest Common Factor?
The HCF is used to simplify the fractions. HCF or GCD is that the greatest number that divides exactly into two numbers.
5. What are the tricks and formulas to find HCF?
The formulas and tricks to find HCF is,
- If the two numbers are said to be co-prime their HCF is 1.
- Product of given two numbers = product of HCF and LCM.
- HCF = HCF of Numerators/LCM of denominators.
