Learning Maths is always fun and interesting. Before going into the topic let us know what is Least Common Multiple is. We are here to help the students enhance their knowledge of maths. We will show different methods to solve the problems on Least Common Multiple(L.C.M).
In arithmetic and number theory, the least common multiple or smallest common multiple of two integers a and b denoted by lcm(a,b) is the smallest positive integer that is divisible by both a and b. Know how to find the LCM of two or more numbers, LCM formula, different methods of LCM, etc from this article. So, students who wish to score high in 5th Grade Math are suggested to read the entire article and solve the questions given below.
Do Refer:
Least Common Multiple Definition
L.C.M is defined as the method to find the least or smallest common multiples in two or more given integers or numbers. The least common multiple is denoted by lcm(a,b).
Let us discuss with an example about LCM.
Example: Find the LCM of 3 and 5.
Solution:
Multiples of 3 are 3, 6, 9, 12, 15, 18…
Multiples of 5 are 5, 10, 15, 20…
Thus the Least Common Multiple of 3 and 5 is 15.
L.C.M Formula
L.C.M is simply the least common multiple. Let a and b be two integers. The formula to find the LCM of a and b is given as,
LCM = (a × b)/GCD(a,b)
Where GCD is the Greatest Common Divisor of a and b.
How to Find the Least Common Multiple?
There are various methods to find the least common multiple of two or more numbers. The three methods to find LCM of the integers is as follows,
1. LCM by listing multiples
2. LCM by prime factorization
3. LCM using division method
Different Methods to find L.C.M
Different methods to find the L.C.M are explained step by step here.
1. LCM by Listing Multiples
By using the listing multiples we can find out the common multiples of two or more numbers. We have to follow some steps to calculate the LCM of two numbers a and b.
Step 1: List a few multiples of a and b.
Step 2: Highlight the common multiples from the multiples of both the numbers.
Step 3: Now select the least common multiple from them. Hence that becomes the L.C.M of two or multiple numbers.
Example: Find the L.C.M of 2 and 3.
Solution:
The multiples of 2 and 3 are as follows,
Multiples of 2 are 2, 4, 6, 8, 10,…
Multiples of 3 are 3, 6, 9, 12…
Thus the least common multiple of 2 and 3 are 6.
2. L.C.M by Prime Factorization
Prime factorization is another method to find the least common multiples of the given numbers. Let us see the example to know what actually the prime factorization is.
Example: Find the L.C.M of 12 and 18.
Solution:
12 = 2 × 2 × 3
18 = 2 × 3 × 3
Thus the LCM of 12 and 18 is 2 × 3 = 6
3. L.C.M by Division Method
Finding the LCM by Division method is an easy method. Follow the steps to find the least common multiples by the division method.
1. Write the numbers separated by commas.
2. Now divide the numbers by the smallest prime number.
3. If any number is not divisible, then write that number below and proceed.
4. Keep on dividing the row of numbers by prime numbers, unless we get the results as 1 in the complete row.
5. Now LCM of the numbers will be equal to the product of all prime numbers in the division method.
Example: Find the L.C.M of 8 and 24.
Solution:
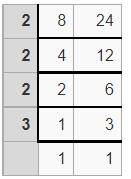
L.C.M of Two Numbers
Let us write the multiples of 3 and 9.
The multiples of 3: 3, 6, 9, 12, 15,…
The multiples of 9: 9, 18, 27, 36,…
From the above two expressions, we can see 3 and 9 have common multiples as 9. There may be more common multiples if we go beyond. The smallest common multiples of 3 and 9 are 9.
L.C.M of Three Numbers
Let us take an example to find the L.C.M of three numbers.
Example: Find the L.C.M of 3, 6, 12.
Solution:
The multiples of 3 are 3, 6, 9, 12, 15, 18,…
The multiples of 6 are 6, 12, 18, 24,…
The multiples of 12 are 12, 24, 36,…
The common multiples of 3, 6, 12 are 12.
Properties of L.C.M
Associative property:
The LCM of two or more numbers will be the same if you change the order of the numbers.
LCM(a, b) = LCM (b,a)
Commutative Property:
LCM(a, b, c) = LCM(LCM(a, b),c) = LCM(a, LCM(b,c))
Distributive Property:
LCM(da, db, dc) = dLCM(a, b, c)
Least Common Multiple Tree
Factors are defined as the numbers that are multiplied together to find the original number. The factor tree method breaks down the numbers into prime numbers.
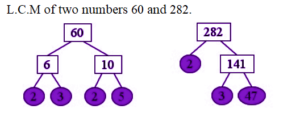
Least Common Multiple (L.C.M) Examples
Example 1.
Find the L.C.M of two numbers 8 and 24 by listing of multiples method.
Solution:
Given the numbers 8 and 24.
We have to find the least common multiples of 8 and 24.
Multiples of 8 are 8, 16, 24, 32, 40,…
Multiples of 24 are 24, 48,….
Thus the least common multiples of 8 and 24 is 24.
Example 2.
Find the L.C.M of two numbers 16 and 64 by the division method.
Solution:
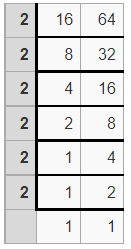
The L.C.M of 16 and 64 is 2 × 2 × 2 × 2 × 2 × 2 = 64
Thus the LCM(16, 64) is 64.
Example 3.
Find the L.C.M of 9 and 18 by the prime factorization method.
Solution:
List all the prime factors for each number.
Prime factorization of 9 is 3 × 3
Prime factorization of 18 is 2 × 3 × 3
For each prime factor, find where it occurs most often as a factor and write it that many times in a new list
LCM of 9 and 18 is 2 × 3 × 3 = 18
Thus the L.C.M of 9 and 18 is 18.
Example 4.
Find the L.C.M of 10 and 20.
Solution:
Given the numbers 10 and 20.
We have to find the least common multiples of 10 and 20.
Multiples of 10 are 10, 20, 30, 40,…
Multiples of 20 are 20, 40, 60,….
Thus the least common multiples of 8 and 24 is 24.
Example 5.
Find the L.C.M of three Numbers 5, 10, 15.
Solution:
List all the prime factors for each number.
Prime factorization of 5 is 5
Prime factorization of 10 is 2 × 5
Prime factorization of 15 is 3 × 5
For each prime factor, find where it occurs most often as a factor and write it that many times in a new list.
The L.C.M of 5, 10, 15 is 2 × 3 × 5 = 30
FAQs on Least Common Multiple(LCM)
1. What is the Least Common Multiple?
It is the smallest of the common multiples of two or more numbers.
2. How to find LCM of numbers?
There are three methods to find the least common multiple of the numbers such as listing the multiples, prime factorization of numbers, and by division method.
3. What is the relation between HCF and LCM?
LCM and HCF are related by the formula:
LCM (a,b) = a × b/HCF(a,b)
Where a and b are two different numbers.
