Everyday Math Grade 3 Answers Unit 9 Multidigit Operations

Everyday Mathematics 3rd Grade Answer Key Unit 9 Multidigit Operations

Everyday Mathematics Grade 3 Home Link 9.1 Answers

Comparing Products

Family Note Today your child learned a game that involves finding a multiplication product greater than the one just played. The activity below provides practice with this skill. Have your child start at the picture of the Minotaur and use a pencil so that he or she can erase wrong turns.

Question 1.
According to Greek mythology, there was a monster called the Minotaur that was half bull and half human. The king had a special mazelike dwelling built, from which the Minotaur could not escape. The dwelling, called a labyrinth (la buh rinth), had many rooms and passageways that formed a puzzle. No one who went in could find their way out without help. One day, a Greek hero named Theseus decided to slay the monster. To find his way out of the labyrinth, Theseus’s friend Ariadne gave him a very, very long ball of string to unwind as he walked through the passageways. After Theseus slew the Minotaur, he followed the string to escape.

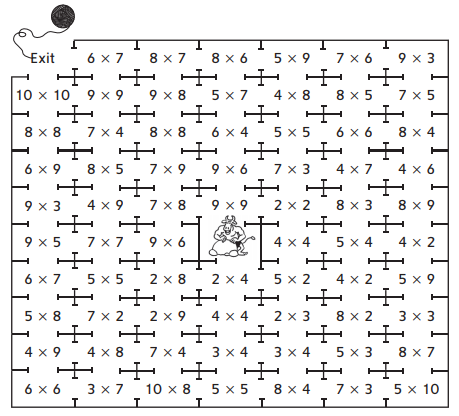
Pretend you are Theseus. To find your way out of the maze, each room you enter must have a product greater than the product in the room you are leaving. Start at the Minotaur’s chambers in the middle and draw a path to the exit.
Answer:

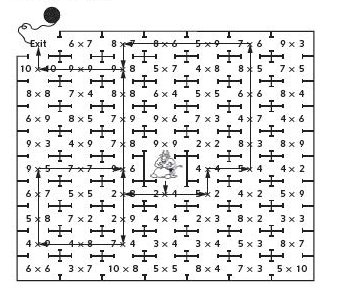
Explanation:
Route I.
2 x 4 = 8
2 x 8 = 16
9 x 6 = 54
7 x 8 = 56
7 x 9 = 63
8 x 8 = 64
9 x 8 = 72
9 x 9 = 81
10 x 10 = 100

Route II.
2 x 4 = 8
2 x 8 = 16
2 x 9 = 18
7 x 4 = 28
4 x 8 = 32
4 x 9 = 36
5 x 8 = 40
6 x 7 = 42
9 x 5 = 45
7 x 7 = 49
9 x 6 = 54
7 x 8 = 56
7 x 9 = 63
8 x 8 = 64
9 x 8 = 72
9 x 9 = 81
10 x 10 = 100

Route III.
2 x 4 = 8
5 x 2 = 10
4 x 4 = 16
5 x 4 = 20
8 x 3 = 24
4 x 7 = 28
6 x 6 = 36
8 x 5 = 40
7 x 6 = 42
5 x 9 = 45
8 x 6 = 48
8 x 7 = 56
9 x 8 = 72
9 x 9 = 81
10 x 10 = 100

The products of the numbers in the rooms must be in an increasing order

Everyday Math Grade 3 Home Link 9.2 Answer Key

Multiplication and Division Number Stories

Family Note Today your child solved number stories involving multiples of 10. The class examined a map displaying the masses of adult North American birds to make sense of the stories and used multiplication/division diagrams to organize information. For the problems below, encourage your child to use a known basic fact to help solve the number models with extended facts involving multiples of 10.

Write a number model. Then solve each number story. You may draw a picture or use the multiplication/division diagram.
Question 1.
One American flamingo has a mass of about 2 kg. What is the mass of 40 American flamingos that each have a mass of about 2 kg?


Answer:

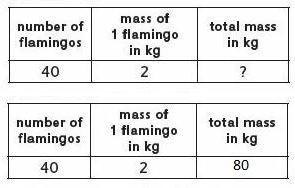
Explanation:
No. of flamingos : 40
Mass of  flamingo : 2 kg
Total mass of flamingos in kg : 40 x 20 = 80 kg

Question 2.
There are 9 bluebirds that each have about the same mass. Together they have a mass of about 270 g. What is the mass of one bluebird?


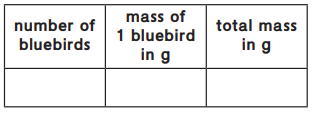
One bluebird has a mass of about _________ g.
Answer:

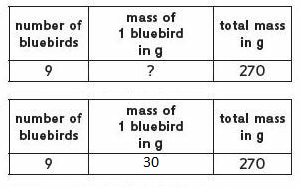
Explanation:
No. of blue birds : 9
total mass of blue birds in kg : 270
mass of 1 blue bird : ?
total mass of blue bird : No. of blue birds x mass of 1 blue bird
9 x ? = 270
taking 9 to the right side of the equation, we get :
270 ÷ 9 = 30
dividing 270 with 9 we get 30

Question 3.
Explain to someone at home how you can use a basic fact to help you solve Problem 2.
Answer:
I though 9 x what number is 270
as 9 x 3 = 27
9 x 30 = 270
by using simple facts i could knw that :
9 x 30 = 270

Everyday Mathematics Grade 3 Home Link 9.3 Answers

Using Mental Math to Multiply

Family Note Today your child practiced applying efficient fact strategies to solve multiplication problems with larger factors. Your child broke apart factors into easier numbers to mentally solve problems involving masses of North American birds.

Solve each problem in your head. Use number models and words to show your thinking.
Question 1.
The mass of one California condor is 9 kilograms. What is the mass of twelve 9-kilogram California condors?
My thinking:

Answer:
108 kg
Explanation :
I know 12 = 6 + 6
So 6 x 9 = 54
We get 12 x 9 = 54 + 54 = 108
So 12 x 9 = 108

Question 2.
The mass of one mountain bluebird is 25 grams. What is the mass of seven 25-gram bluebirds?
My thinking:

Answer:
175 grams
Explanation :
I broke apart 7 into 4 and 3
I know 25 x 4 = 100
25 x 3 = 75
so 7 x 25 = 200 + 75 = 175
I used the break apart strategy and thought :
25 x 7 = 20 x 7 + 5 x 7
= 140 + 35
= 175
so 25 x 7 = 175
= 175 grams

Question 3.
Explain to someone at home how you can use the break-apart and doubling strategies to solve problems with larger factors.
Answer:

Everyday Math Grade 3 Home Link 9.4 Answer Key

Measuring the Lengths of Activities

Family Note Today your child practiced measuring time intervals by planning a schedule for a field trip. After completing Problem 1, have your child explain how he or she figured out the length of each activity.

Question 1.
Isabella wants to know how long each camp activity lasts. Use the table below to find the length of each activity. You may use open number lines, clocks, or another strategy.

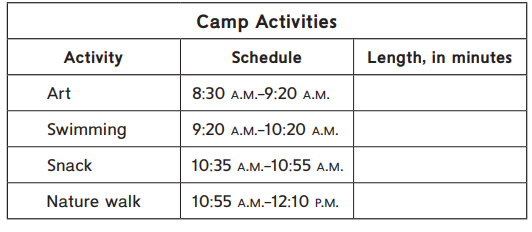
Answer:

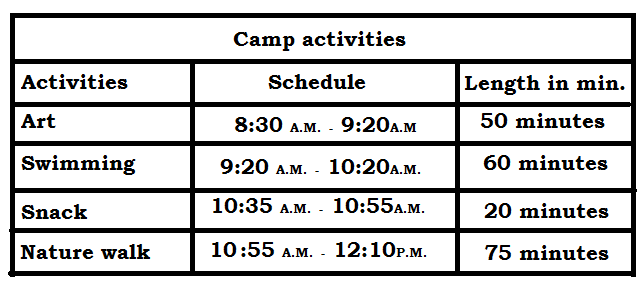
Explanation:

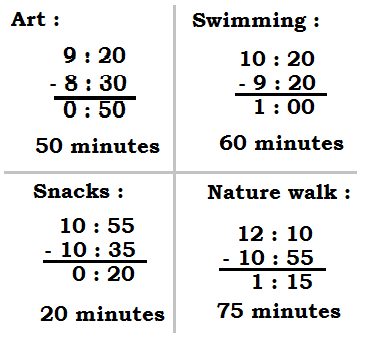
Practice
Solve.
Question 2.
4 × 60 = ________
Answer:
4 x 60 = 240
Explanation:
we know 6 x 4 = 24
this helps us know 4 x 60
4 x 60 = 240

Question 3.
70 × 3 = __________
Answer:
70 x 3 = 210
Explanation:
we know that 7 x 3 = 21
this helps us know 3 x 70
3 x 70 = 210

Question 4.
________ = 60 × 8
Answer:
480 = 60 x 8
Explanation:
we know that 6 x 8 = 48
this helps us know 60 x 8
60 x 8 = 480

Question 5.
_________ = 80 × 9
Answer:
80 x 9 = 720
Explanation:
we know that 8 x 9 = 72
this helps us know 80 x 9
80 x 9 = 720

Everyday Mathematics Grade 3 Home Link 9.5 Answers

Multidigit Multiplication

Family Note Today your child multiplied 2-digit numbers by 1-digit numbers using area models. Children drew a rectangle to represent the multiplication problem and then broke apart the larger factor into smaller, easier-to-multiply numbers.

Use the break-apart strategy to solve the multiplication problems. Draw and partition a rectangle. Then record number sentences to show how you broke apart the factor.

Example:
3 × 28 = 84

Two ways to break apart 28 to help solve 3 × 28.

Question 1.
5 × 42 = _________
Answer:
5 x 42 = 210
Explanation:

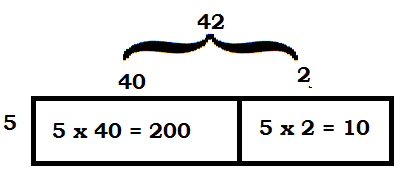
we broke 42 apart into 40 and 2 for easier multiplication
5 x 40 = 200
5 x 2 = 10
200 + 10 = 210
so we know that 5 x 42 = 210

Question 2.
6 × 54 = _________
Answer:
6 x 54 = 324
Explanation:

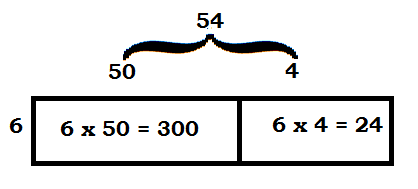
we broke apart 54 into 50 and 4
50 x 6 = 300
4 x 6 = 24
300 + 24 = 324
so we know that 54 x 6 = 324

Question 3.
Explain to someone at home how you broke apart the larger factors.
Answer:
I broke apart the larger factors into the nearest 10’s and the remaining number
Explanation:
Ex: 67
67 is divided into its nearest 10’s : 60
the remaining number is 67 – 60 = 7
so we divided 67 into 60 and 7

Everyday Math Grade 3 Home Link 9.6 Answer Key

Using Tools Effectively

Family Note Today your child pretended to use a calculator with a broken division key to solve a number story. In the problem below, your child is asked to solve a similar problem with a broken calculator. Ask your child to explain why both strategies work and how they are different.

Ask someone at home for a calculator you can use to solve this problem.

A third-grade class is planning to buy eggs for the school’s pancake breakfast. They need 180 eggs for the breakfast. The teacher reminded the class that eggs come in cartons of 12 and asked them to figure out how many cartons they need. Lucy wants to use her calculator to solve the problem, but the and keys are both broken. Help Lucy find a way to use her broken calculator to solve the problem.
Question 1.
Show or tell how to use Lucy’s broken calculator to find the number of cartons of eggs the class needs to buy.
The class needs to buy _________ cartons of eggs.
Answer:
15 cartoons
Explanation:
I knew that the number of cartoons had to be more than 10
because 10 x 12 = 120 and the class needed 180 eggs
so I tried 12 x 12 on the calculator but it was only 144
so I tried 12 x 13, 12 x 14 and 12 x 15
12 x 15 = 180
so 15 is the number of cartoons needed for the class

Question 2.
Show or tell another way for Lucy to use her broken calculator to solve the problem.
Answer:
as we know that only – and x keys are working we can
180 – 12 = 168
if we do it over and over again after subtracting 12 15 times the answer will become 0
180 – 12 = 168       (1)
168 – 12 = 156       (2)
156 – 12 = 144       (3)
144 – 12 = 132       (4)
132 – 12 = 121       (5)
120 – 12 = 108       (6)
108 – 12 = 96         (7)
96   – 12 = 84         (8)
84   – 12 = 72         (9)
72   – 12 = 60         (10)
60   – 12 = 48         (11)
48   – 12 = 36         (12)
36   – 12 = 24         (13)
24   – 12 = 12         (14)
12   – 12 = 0           (15)

by subtracting 12 from 180 over and over again after subtracting 15 times the answer will become 0

Everyday Mathematics Grade 3 Home Link 9.7 Answers

Calculating Elapsed Time

Family Note Throughout the year, your child has practiced calculating the length of day (hours of sunlight) using sunrise and sunset data. Children have used clocks and open number lines to figure out the total minutes and hours that pass from a start time to an end time. Today children analyzed graphs showing the length-of-day data for our location and for other locations around the world.

Question 1.
On the map below, look at the sunrise and sunset times for December 21, 2016. On the back of this page, calculate the length of day for all three cities. Record the times next to each city on the map.

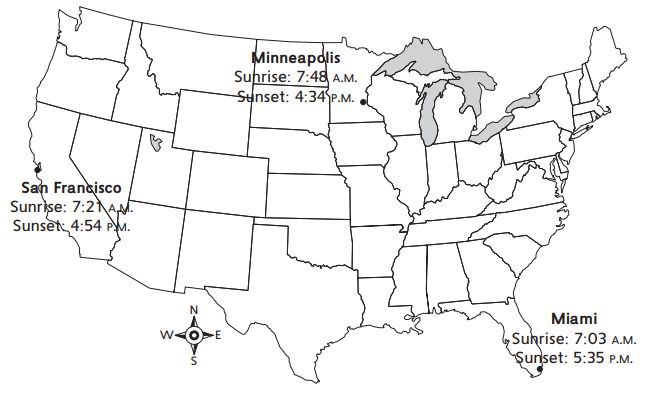
Answer:

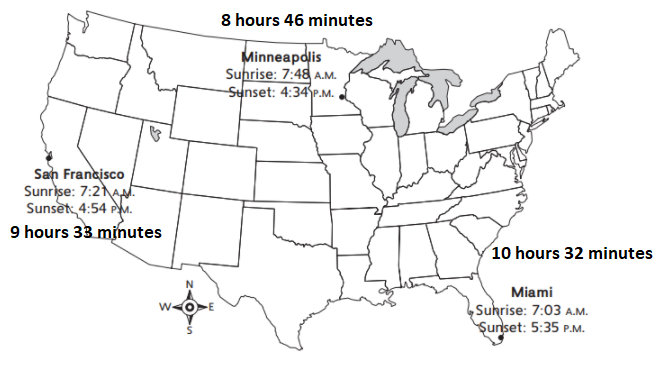
Explanation:
San Francisco :

9 hours 33 minutes
Minneapolis :

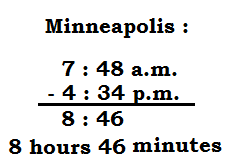
8 hours 46 minutes
Miami :

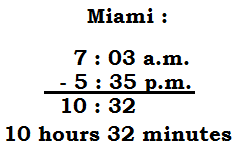
10 hours 32 minutes

Question 2.
Which city has the most hours of sunlight?
Answer:
Miami
Explanation :
Miami has day light for 10 hours 32 minutes

Question 3.
Which city has the least hours of sunlight?
Answer:
Minneapolis
Explanation :
Minneapolis has day light for 8 hours 46 minutes