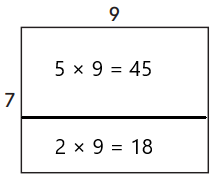Everyday Mathematics 3rd Grade Answer Key Unit 5 Fractions and Multiplication Strategies
Everyday Mathematics Grade 3 Home Link 5.1 Answers
Fractions of a Whole
Family Note Today your child worked with fraction circle pieces to explore fractions as equal parts of wholes. Children covered fraction circle pieces with equal parts and described the parts using fraction words such as 1-third. Standard notation for fractions, such as \(\frac{1}{3}\) , will be introduced in the next lesson. As your child works on this activity, discuss the fraction names of the equal parts in each problem.
Write fraction words to describe the shaded part.
Question 1.
The circle is the whole.
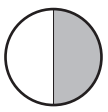
A fraction that names the shaded part is __________
Answer:
A fraction that names the shaded part is 1/2.
Explanation:
Here, we can see that the circle was divided into two parts. So the fraction that names the shaded part is 1/2.
Question 2.
The square is the whole.
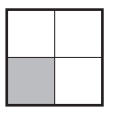
A fraction that names the shaded part is ____________
Answer:
A fraction that names the shaded part is 1/4.
Explanation:
Here, we can see that the square was divided into four parts and one part was shaded. So the fraction that names the shaded part is 1/4.
Question 3.
The rectangle is the whole.
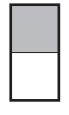
A fraction that names the shaded part is ___________
Answer:
A fraction that names the shaded part is 1/2.
Explanation:
Here, we can see that the rectangle was divided into two parts and one part was shaded. So the fraction that names the shaded part is 1/2.
Practice
Fill in the unit box. Solve these problems mentally, or use counting-up, expand-and-trade , or trade-first subtraction.
Question 4.
________ = 326 – 291
Answer:
326 – 291 = 35.
Explanation:
The difference between 326 and 291 is 35.
Question 5.
________ = 391 – 226
Answer:
391 – 226 = 165.
Explanation:
The difference between 391 and 226 is 165.
Everyday Math Grade 3 Home Link 5.2 Answer Key
Representing Fractions
Family Note Today your child learned how to represent fractions in words, in standard notation (\(\frac{1}{2}\), \(\frac{3}{4}\), and so on), and with drawings. For each of the problems below, the whole is a different shape. Help your child relate each fraction representation to the number of equal-size parts each whole is divided into and the number of shaded equal parts.
Complete the table.
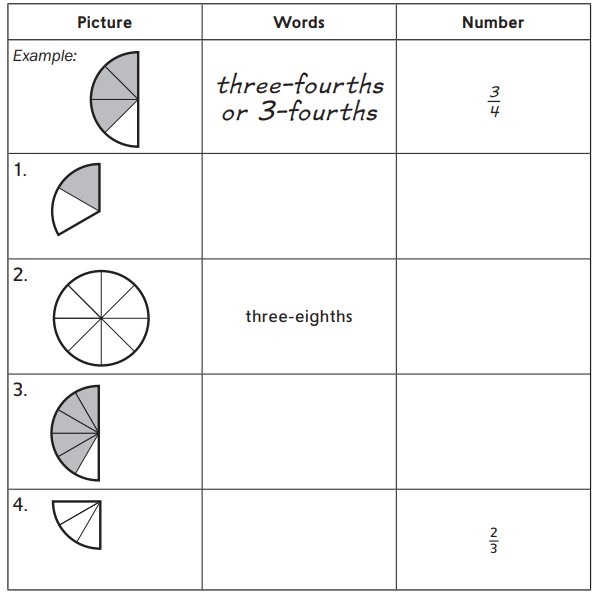
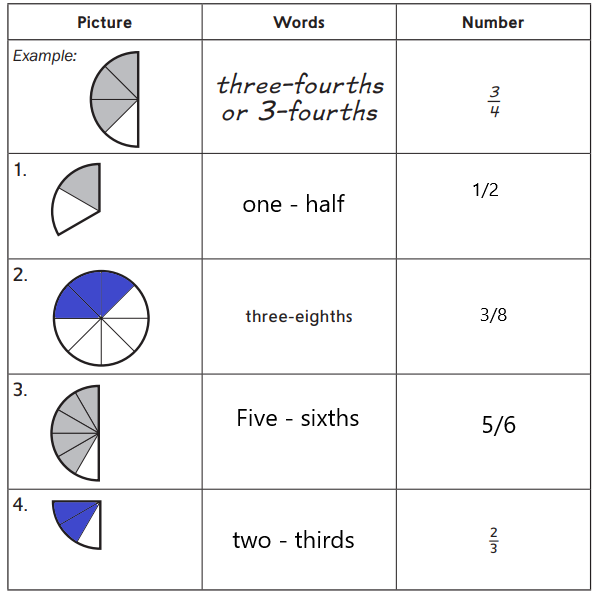
Answer:
Everyday Mathematics Grade 3 Home Link 5.3 Answers
Equivalent Fractions
Family Note Today your child continued working with fractions by finding different fractions that name the same amount of the whole, or equivalent fractions. Children identify equivalent fractions by looking at the shaded area of a figure compared to the shaded area of another same-size figure.
The pictures show three kinds of fruit pie. Use a straightedge to do the following:
Question 1.
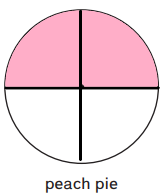
Divide the peach pie into 4 equal pieces. Shade 2 of the pieces.
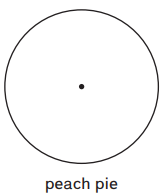
Answer:
The fraction of the peach pie is 2/4.
Explanation:
Here, we have a peach pie and divided that peach pie into 4 equal pieces then we have shaded 2 of the pieces. And here the fraction of the peach pie is 2/4.
Question 2.
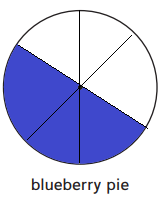
Divide the blue berry pie into 6 equal pieces. Shade 3 of the pieces.

Answer:
The fraction of the blueberry pie is 3/6.
Explanation:
Here, we have a blueberry pie and divided that peach pie into 6 equal pieces then we have shaded 3 of the pieces. And here the fraction of the peach pie is 3/6.
Question 3.
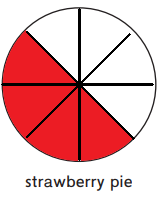
Divide the strawberry pie into 8 equal pieces. Shade 4 of the pieces.
Answer:
The fraction of the strawberry pie is 4/8.
Explanation:
Here, we have a strawberry pie and divided that peach pie into 8 equal pieces then we have shaded 4 of the pieces. And here the fraction of the peach pie is 4/8.
What fraction of each pie did you shade?
Question 4.
I shaded _________ of the peach pie.
Write another name for this fraction: _________
Answer:
I shaded 2/4 of the peach pie. The other name for the fraction is 0.5.
Explanation:
Here, we have a peach pie and divided that peach pie into 4 equal pieces then we have shaded 2 of the pieces. And here the fraction of the peach pie is 2/4. The other name for the fraction is 0.5.
Question 5.
I shaded _________ of the blueberry pie.
Write another name for this fraction: _________
Answer:
I shaded 3/6 of the blueberry pie. The other name for the fraction is 0.5.
Explanation:
Here, we have a blueberry pie and divided that peach pie into 6 equal pieces then we have shaded 3 of the pieces. And here the fraction of the peach pie is 3/6. The other name for the fraction is 0.5.
Question 6.
I shaded _________ of the strawberry pie.
Write another name for this fraction: _________
Answer:
I shaded 4/8 of the strawberry pie. The other name for the fraction is 0.5.
Explanation:
Here, we have a strawberry pie and divided that peach pie into 8 equal pieces then we have shaded 4 of the pieces. And here the fraction of the peach pie is 4/8. The other name for the fraction is 0.5.
Explain to someone at home how you know that all of the fractions on this page are equivalent.
Answer:
Here to that, all of the fractions on this page are equivalent or not, we will multiply the numerator of one fraction by the denominator of the other fraction and we can also multiply the denominator of one fraction by the numerator of the other fraction.
Everyday Math Grade 3 Home Link 5.4 Answer Key
Identifying Helper Facts
Family Note Today your child practiced identifying and using helper facts to solve unknown multiplication facts by adding or subtracting a group. For example, children added a group to “helper” 2s and 5s facts to solve 3s and 6s facts. They subtracted a group from “helper” 5s and 10s facts to solve 4s and 9s facts. Practice with efficient fact strategies such as these helps children become fluent with all multiplication facts.
For each fact below:
- Think of a helper fact.
- Add or subtract a group from the product of the helper fact .
- Solve the fact.
Example: 6 × 7 = ?
Helper fact: 5 × 7 = 35
How I can use it: I can add one more group of 7 to 35 to get 35 + 7 = 42.
6 × 7 = 42
Question 1.
3 × 8 = ?
Helper fact: __________
How I can use it: __________
3 × 8 = __________
Answer:
Example: 3 × 8 = ?
Helper fact: 2 × 8 = 16.
How I can use it: Here, we can add one more group of 8 to 16 to get 16 + 8 = 24.
3 × 8 = 24.
Explanation:
Here, we have added one more group of 8 to 16 to get 16 + 8 = 24.
Question 2.
9 × 7 = ?
Helper fact: __________
How I can use it: __________
9 × 7 = __________
Answer:
Example: 9 × 7 = ?
Helper fact: 8 × 7 = 56.
How I can use it: Here, we can add one more group of 9 to 56 to get 56 + 9 = 63.
9 × 7 = 63.
Explanation:
Here, we have added one more group of 9 to 56 to get 56 + 9 = 63.
Everyday Mathematics Grade 3 Home Link 5.5 Answers
Doubling, Part 1
Family Note Doubling (adding a number to itself or multiplying a number by 2) can be used as a strategy to solve facts with a “double” as a factor, such as the 4s, 6s, and 8s facts. For example, your child used doubling with the helper fact 2 × 7 to figure out 4 × 7 (2 × 7 = 14 and 14 + 14 = 28, so 4 × 7 = 28). Doubling the area of a rectangle can help children see and model the doubling fact strategy. Encourage your child to use drawings to solve the problem below.
Question 1.
Maria wants to figure out 4 × 6 = ?.
She notices that 4 is the double of 2.
Help Maria use 2 × 6 to solve 4 × 6.
Maria starts by sketching a 2-by-6 rectangle. Add to Maria’s picture to show how she could use doubling to find the answer to 4 × 6. Record your thinking below.
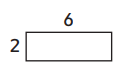
2 × 6 = __________
4 × 6 = __________
How I figured it out: __________
Answer:
2 × 6 = 12
4 × 6 = 24
How I figured it out: By doubling the 2 by 6 rectangle.
Explanation:
Here, we have doubled the 2 by 6 rectangle, so that we can find 4 by 6 value. So we can get the value by doubling the value of 2 by 6.
Everyday Math Grade 3 Home Link 5.6 Answer Key
Doubling, Part 2
Family Note Today your child continued to work on the doubling facts strategy with facts that have even factors. Your child broke apart an even factor into two identical factors and used the resulting helper fact to derive the final product. For example, 6 × 7 can be broken into 3 × 7 and 3 × 7, making the total easier to find
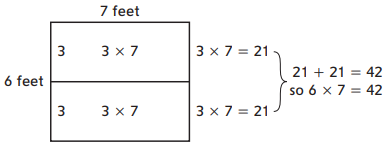
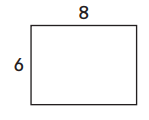
Question 1.
Show how you can solve 8 × 6 using doubling.
Factor I will split in half: __________
Sketch:
8 × 6 = __________
What helper fact did you double to solve 8 × 6?
Answer:
The factor I have split in half is 6 × 8 as 3 × 8 and 3 × 8.
Explanation:
Here, we have split 6 as 3 and 3. As 3 + 3 is 6, so here we have used doubling the facts strategy with facts that have even factors. So we will make as 3 × 8 = 24 and 3 × 8 = 24 which is 48 and 6 × 8 = 48.
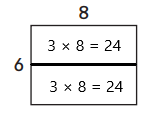
Everyday Mathematics Grade 3 Home Link 5.7 Answers
Patterns in Products
Family Note Today your child used number grids and the Multiplication/Division Facts Table to explore patterns in multiples of 5s, 9s, and 10s, as well as in products of even and odd numbers. Recognizing and making sense of patterns is an important part of mathematics. Understanding the patterns in these products will also help your child become more fluent with multiplication facts.
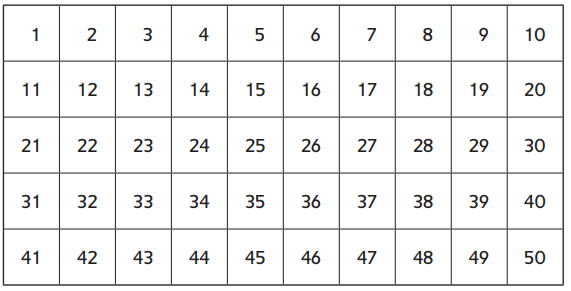
Question 1.
Circle the products of 10 × 1, 10 × 2, 10 × 3, 10 × 4, and 10 × 5.
Answer:
Circled the products which are 10, 20, 30, 40, 50.
Explanation:
Here, we have circled the products of 10 × 1, 10 × 2, 10 × 3, 10 × 4, and 10 × 5 which are 10, 20, 30, 40, 50.
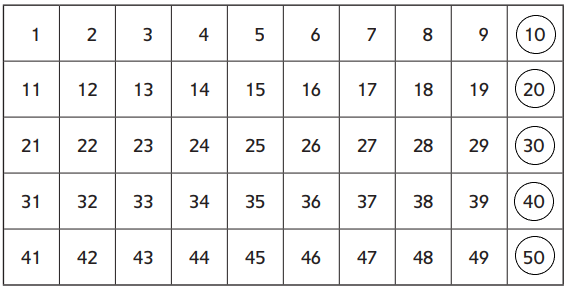
Question 2.
Shade the products of 9 × 1, 9 × 2, 9 × 3, 9 × 4, and 9 × 5.
Answer:
We have shaded the products which are 9, 18, 27, 36, 45.
Explanation:
Here, we have shaded the products of 9 × 1, 9 × 2, 9 × 3, 9 × 4, and 9 × 5 which are 9, 18, 27, 36, 45.
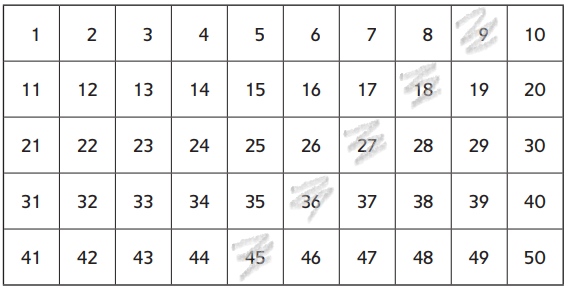
Question 3.
Explain why the pattern for the products of 10s facts is a straight column.
Answer:
The pattern for the products of 10s facts is a straight column because we are multiplying 10’s and we are basically adding another 10 each time and the numbers grid is in rows of 10 and adding another 10 is the same as moving down one row which makes a straight column.
Question 4.
Explain why the pattern for the products of 9s facts is a diagonal.
Hint: Think of how it compares to the products of the 10s facts pattern.
Answer:
As the multiples of 9 are one less than 10 away from each other. So the patterns for the products of 9’s facts are diagonal.
Everyday Math Grade 3 Home Link 5.8 Answer Key
Finding Missing Factors
Family Note Today your child played the game Salute! to practice finding missing factors. Determining missing factors in multiplication equations can help children develop fluency with multiplication and division. Help your child use the given factor and product to determine the missing factor in each problem below. For example, in Round 1 have your child think: 5 times what number is 2 5?
If you want to play Salute! with your child, the directions are on Student Reference Book, page 255. Use a regular deck of playing cards. Remove all face cards and jokers. The aces are 1s.
Question 1.
Write the missing factors for the rounds of Salute!
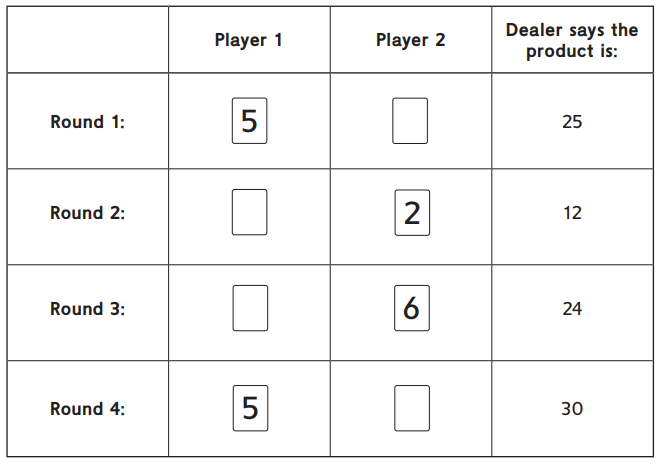
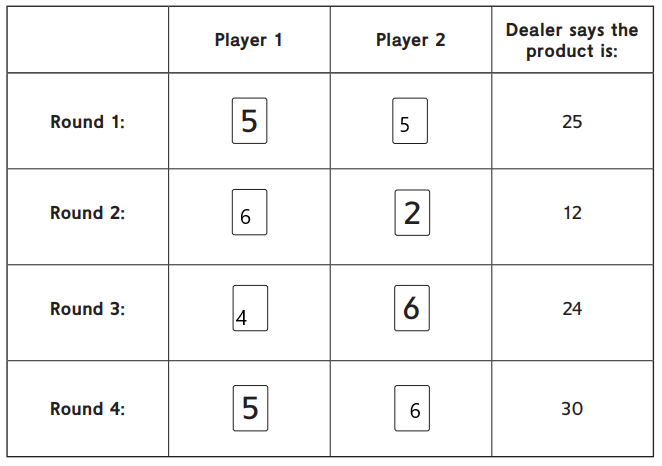
Explain how you found the missing factor for one of the rounds.
Answer:
Here, we have found the missing factor by dividing the given player and the product that the dealer says.
Everyday Mathematics Grade 3 Home Link 5.9 Answers
Near Squares
Family Note Today your child learned to use familiar multiplication squares, such as 3 × 3 = 9 and 8 × 8 = 64, to figure out near-squares facts by adding or subtracting groups. For example, the square 8 × 8 = 64 can be used as a helper fact for the near square 7 × 8. By subtracting one group of 8 from 64, children find that 7 × 8 = 56. Using squares as helper facts is one more strategy in your child’s growing library of multiplication facts strategies.
Example: 4 × 3 = ?
Square helper fact: 3 × 3 = 9
Near square: 4 × 3 = 12

How I solved it: I added a group of 3 to find 4 × 3.
Question 1.
Solve the multiplication squares.
5 × 5 = ____________
6 × 6 = ____________
Answer:
5 × 5 = 25.
helper fact is 4 × 5 = 20.
6 × 6 = 36.
helper fact is 5 × 6 = 30.
Explanation:
Here, we have used helper fact for the near square by subtracting one group of 5 from 25 and by subtracting one group of 6 from 30.
Question 2.
Choose one of the squares facts from Problem 1. Write a near square and use your square to help solve the near square. Show your work.
Square helper fact: ________ × ________ = ________
Near square: ________ × ________ = ________
How I solved it:
Answer:
Square helper fact: 9 × 9 = 81
Near square: 8 × 9 = 72
How I solved it: By subtracting one group of 9 from 81.
Explanation:
Here, we have used helper fact for the near square by subtracting one group of 9 from 81 and by subtracting one group of 9 from 72.
Everyday Math Grade 3 Home Link 5.10 Answer Key
Making Sense of a Problem
Family Note Today your child solved a challenging number story. To solve it, your child had to make sense of the information in the problem. If your child has trouble getting started on the problems below, ask: What does the problem tell you? What do you need to find out? Encourage your child to draw a picture to show what he or she understands about each problem.
Question 1.
Danika lives 5 blocks from her school. If she walks to and from school 5 days each week, how many blocks does she walk in one week?
__________ (unit)
Answer:
Danika walks 50 units to and from school 5 days each week.
Explanation:
Here, Danika lives 5 blocks from her school, and if she walks to and from school 5 days each week. So the number of blocks does she walk in one week is 5 × 5= 25 blocks. So, Danika walks 25 + 25 = 50 blocks to and from school 5 days each week.
Question 2.
It costs $5 to join the art club. The club has collected $70 from new members. The club’s goal is to collect $100. How many more members does the club need to meet its goal?
__________ (unit)
Answer:
The club needed 6 more members to meet the goal.
Explanation:
Here, the cost to join the art club is $5 and the club has collected $70 from new members. And the club’s goal is to collect $100, so the club needs to collect $100 – $70 = $30. So the club needed a number of more members to meet the goal is 30 ÷ 5 = 6 more members.
Everyday Mathematics Grade 3 Home Link 5.11 Answers
The Break-Apart Strategy
Family Note Today your child learned how to break apart one number in a multiplication fact in order to make two helper facts that are easier to solve. Using areas of rectangles helps to illustrate this, as in the example below.
7 × 6 = ?
- Break apart the 7 into 5 and 2.
- There are two helper facts: 5 × 6 and 2 × 6.
- So 7 × 6 = 5 × 6 + 2 × 6
7 × 6 = 30 + 12
7 × 6 = 42
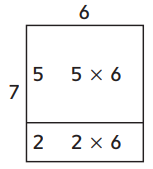
Question 1.
Show one way you can solve 7 × 9 = ?.
I will break apart the factor __________ into __________ and __________.
Helper facts that match the areas of the smaller rectangles:
__________ × __________ = __________ and __________ × __________ = __________
Drawing:
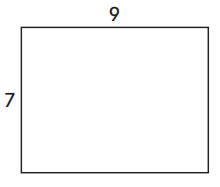
Write a number model using your helper facts:
7 × 9 = ______ × ______ + ______ × ______
7 × 9 = ______
Answer:
I will break apart the factor 7 into 5 and 2.
Helper facts that match the areas of the smaller rectangles:
5 × 9 = 45 and 2 × 9 = 18.
7 × 9 = 5 × 9 + 2 × 9
7 × 9 = 63.
Explanation:
Here, we will break apart factor 7 into 5 and 2 and we will match the areas of the smaller rectangles as
5 × 9 = 45 and 2 × 9 = 18.
7 × 9 = 5 × 9 + 2 × 9
7 × 9 = 63.