Everyday Mathematics 4th Grade Answer Key Unit 2 Multiplication and Geometry
Everyday Math Grade 4 Home Link 2.1 Answer Key
Exploring Square Numbers
A square number is a number that can be written as the product of a number multiplied by itself. For example, the square number 9 can be written as 3 ∗ 3.
Question 1.
Fill in the missing factors and square numbers.
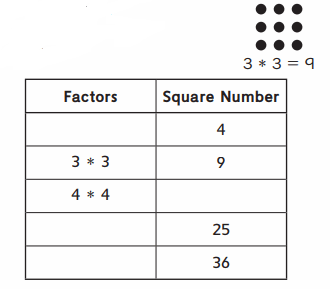
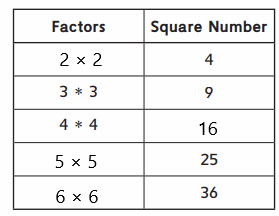
Answer:
We will fill the blanks factors and square numbers.
Explanation:
As the square number is a number that can be written as the product of a number multiplied by itself. So, here we will fill the blanks factors and square numbers.
Question 2.
What pattern(s) do you see in the factors? In the products?
Answer:
The pattern do we see in the factors is Prime Factorization.
Explanation:
Here, in the above table, we have used the Prime Factorization pattern. The Prime Factorization method is defined as a way of finding prime numbers, which are multipled together to get the original number.
Question 3.
What other pattern(s) do you see in the table?
Answer:
The other pattern that we have seen in the table is the squares of the numbers.
Question 4.
Write an equation to describe each array.
a. 
Equation: ___
Answer:
The equation will be 4 × 9 = 36.
Explanation:
As we have 36 dots in all and there are 4 rows with 9 dots in each row. So the equation will be 4 × 9 which is 36 dots.
b. 
Equation: ___
Answer:
The equation will be 5 × 5 = 25.
Explanation:
As we have 25 dots in all and there are 5 rows with 5 dots in each row. So the equation will be 5 × 5 which is 25 dots.
Question 5.
a. Which of the arrays above shows a square number? ___________
b. Explain. ________
Answer:
a. The above arrays that show a square number is array b.
b. As there are 5 rows of 5 dots which is 25 dots.
Explanation:
In the above arrays that show a square number is array b as there are 5 rows of 5 dots which is 25 dots.
Practice
Question 6.
32, 45, 58, ____, ____, ____ Rule: _____
Answer:
32, 45, 58, 71, 84, 97.
Rule: Adding 13.
Explanation:
Here, we need to add 13. If we check the difference between 45 and 32 we will get the difference as 13. So, we can see that in the given series, so 13 is added to the given numbers. So the rule is adding 13.
Question 7.
___, ___, ___, 89, 115, 141 Rule: ____
Answer:
11,37,63,89,115,141
Rule: subtract 26.
Explanation:
Here, we need to subtract 26. If we check the difference between 141 and 115 we will get the difference as 26. So, we can see that in the given series, so 26 is subtracted to the given numbers. So the rule is subtracting 26.
Everyday Math Grade 4 Home Link 2.2 Answer Key
Area of a Rectangle
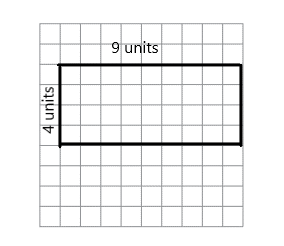
Question 1.
Draw a rectangle that has length of 9 units and width of 4 units.

Equation: ___
Area = ___ square units
Answer:
The area of the rectangle is 36 square units.
Explanation:
Here, we have constructed a rectangle that has a length of 9 units and a width of 4 units. And here we need to find the area of the rectangle, so the area of the rectangle is
Area = length × breadth
= 9 × 4
= 36 square units.
So the area of the rectangle is 36 square units.
Question 2.
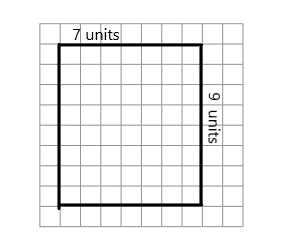
Draw a rectangle that has a length of 7 units and a width of 8 units.
Equation: ___
Area = ___ square units
Answer:
The area of the rectangle is 56 square units.
Explanation:
Here, we have constructed a rectangle that has a length of 7 units and a width of 8 units. And here we need to find the area of the rectangle, so the area of the rectangle is
Area = length × breadth
= 7 × 8
= 56 square units.
So the area of the rectangle is 56 square units.
Use the formula A = I ∗ w to find the area of each rectangle.
Question 3.
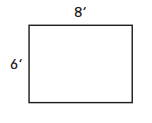
Equation: ___
Area = ___ square units
Answer:
The area of the rectangle is 48 square units.
Explanation:
Here, we need to find the area of the rectangle, so the area of the rectangle is
Area = length × breadth
= 8 × 6
= 48 square units.
So the area of the rectangle is 48 square units.
Question 4.
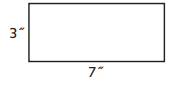
Equation: ___
Area = ___ square units
Answer:
The area of the rectangle is 48 square units.
Explanation:
Here, we need to find the area of the rectangle, so the area of the rectangle is
Area = length × breadth
= 8 × 6
= 48 square units.
So the area of the rectangle is 48 square units.
Question 5.
Riley’s dining room tabletop is 9 feet long and 6 feet wide. What is the area of the tabletop?
Equation: _____
Area = ___ square feet
Answer:
The area of the tabletop is 54 square feet.
Explanation:
Riley’s dining table top is 9 feet long and width is 6 feet, so the area of the tabletop is
Area = length × width
= 9 × 6
= 54 square feet.
So the area of the tabletop is 54 square feet.
Practice
Question 6.
368 – 59 = ____
Answer:
The subtraction of two numbers is 309.
Explanation:
By subtracting the given numbers 368 – 59 we will get the result as 309.
Question 7.
194 – 147 = ___
Answer:
The subtraction of two numbers is 47.
Explanation:
By subtracting the given numbers 194 – 147 we will get the result as 47.
Question 8.
____ = 1,729 – 623
Answer:
The subtraction of two numbers is 1,106.
Explanation:
By subtracting the given numbers 1,729 – 623 we will get the result as 1,106.
Everyday Math Grade 4 Home Link 2.3 Answer Key
Working with Factor Pairs
Write equations to help you find all the factor pairs of each number below. Use dot arrays, if needed.
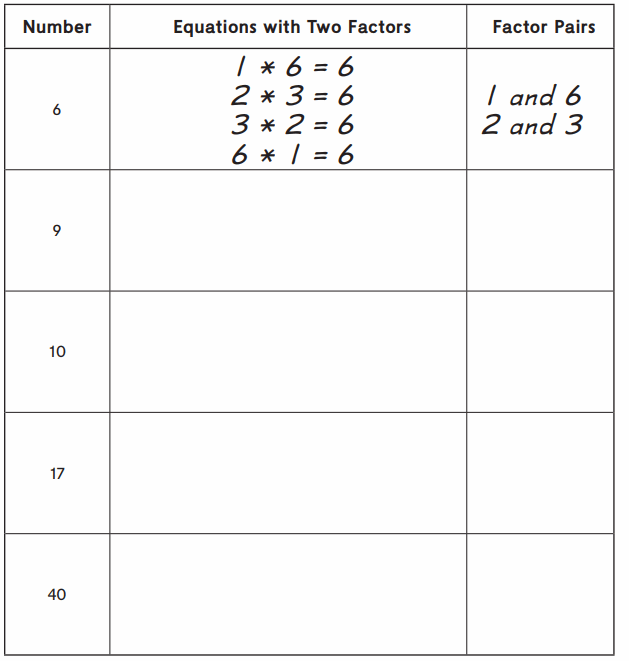
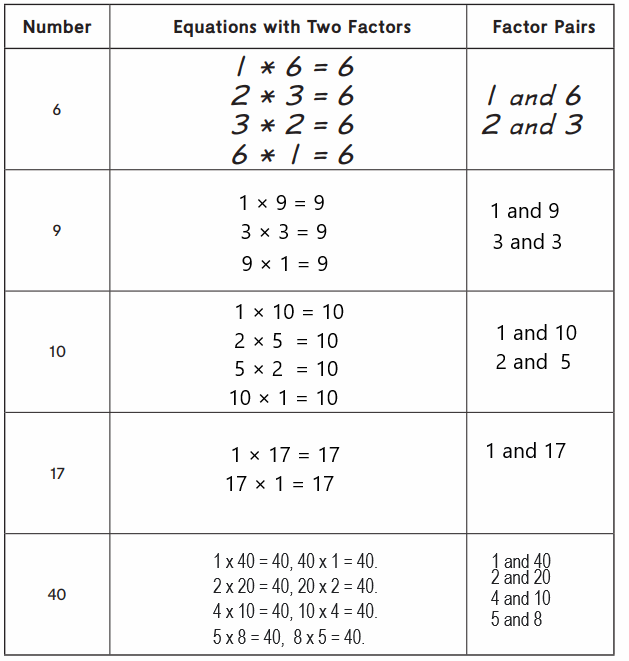
Practice
Question 2.
356 + 433 = ___
Answer:
The addition of two numbers is 789.
Explanation:
The addition of the two given numbers 356 + 433 is 789.
Question 3.
___ = 2,167 + 696
Answer:
The addition of two numbers is 2,863.
Explanation:
The addition of the two given numbers 2,167 + 696 is 2,863.
Question 4.
___ = 4,578 – 2,232
Answer:
The subtraction of two numbers is 2,346
Explanation:
The subtraction of the two given numbers 4,578 – 2,232 is 2,346.
Question 5.
3,271 – 1,089 = ___
Answer:
The subtraction of two numbers is 2,182.
Explanation:
The subtraction of the two given numbers 4,578 – 2,232 is 2,182.
Everyday Math Grade 4 Home Link 2.4 Answer Key
Finding Multiples
Question 1.
List the first 5 multiples of 4. ____________
Answer:
4 × 1 = 4,
4 × 2 = 8,
4 × 3 = 12,
4 × 4 = 16,
4 × 5 = 20.
Explanation:
The first 5 multiples of 4 are:
4 × 1 = 4,
4 × 2 = 8,
4 × 3 = 12,
4 × 4 = 16,
4 × 5 = 20.
Question 2.
List the first 10 multiples of 2. _______________
Answer:
2 × 1 = 2,
2 × 2 = 4,
2 × 3 = 6,
2 × 4 = 8,
2 × 5 = 10,
2 × 6 = 12,
2 × 7 = 14,
2 × 8 = 16,
2 × 9 = 18,
2 × 10 = 20.
Explanation:
The first 10 multiples of 2 is
2 × 1 = 2,
2 × 2 = 4,
2 × 3 = 6,
2 × 4 = 8,
2 × 5 = 10,
2 × 6 = 12,
2 × 7 = 14,
2 × 8 = 16,
2 × 9 = 18,
2 × 10 = 20.
Question 3.
a. List the first 10 multiples of 3. _________
Answer:
3 × 1 = 3,
3 × 2 = 6,
3 × 3 = 9,
3 × 4 = 12,
3 × 5 = 15,
3 × 6 = 18,
3 × 7 = 21,
3 × 8 = 24,
3 × 9 = 27,
3 × 10 = 30.
Explanation:
The first 10 multiples of 3 is
3 × 1 = 3,
3 × 2 = 6,
3 × 3 = 9,
3 × 4 = 12,
3 × 5 = 15,
3 × 6 = 18,
3 × 7 = 21,
3 × 8 = 24,
3 × 9 = 27,
3 × 10 = 30.
b. List the first 10 multiples of 5. _________
Answer:
5 × 1 = 5,
5 × 2 = 10,
5 × 3 = 15,
5 × 4 = 20,
5 × 5 = 25,
5 × 6 = 30,
5 × 7 = 35,
5 × 8 = 40,
5 × 9 = 45,
5 × 10 = 50.
Explanation:
The first 10 multiples of 5
5 × 1 = 5,
5 × 2 = 10,
5 × 3 = 15,
5 × 4 = 20,
5 × 5 = 25,
5 × 6 = 30,
5 × 7 = 35,
5 × 8 = 40,
5 × 9 = 45,
5 × 10 = 50.
c. List the multiples of 3 that are also multiples of 5. ________
Answer:
Multiples of 3 that are also multiples of 5 are 15, 30, 45, 60, 75, 90.
Explanation:
The multiples of 3 that are also multiples of 5 are 15, 30, 45, 60, 75, 90.
Question 4.
Is 28 a multiple of 7? ___ Explain. ______
Answer:
Yes, 28 is a multiple of 7.
Explanation:
Yes, 28 is a multiple of 7. As 28 is divisible by 7 and when we divide 28 by 7 we will get the reminder as zero. So 28 is a multiple of 7.
Question 5.
Is 35 a multiple of 6? __ Explain. _____
Answer:
No, 35 is not a multiple of 6.
Explanation:
No, 35 is not a multiple of 6. As 35 is not divisible by 6 and when we divide 35 by 6 we will not get the reminder as zero. So 35 is not divisible by 6.
Question 6.
a. List the factors of 15. List the multiples through 15 of each factor.


b. Is 15 a multiple of each of its factors? Explain.
Answer:
Yes, 15 is a multiple of each of its factors.
Explanation:
Yes, 15 is a multiple of each of its factors. As 15 is divisible by 1, 3, 5, 15, and by dividing we will get the reminder as zero. So 15 is a multiple of each of its factors.
Practice
Question 7.
24, ____, 48, ___, 72, ___ Rule: ____
Answer:
24, 36, 48, 72, 84.
Rule: Adding 12.
Explanation:
Here, we will add 12 to the given number 24 then we will get 36 and then we will add 12 to the number 36 then we will get 48 and we will continue until we will get the last number. So here the rule is adding 12.
Question 8.
___, 108, 162, ___, 270, ___ Rule: ____
Answer:
54, 108, 162, 216, 270, 324.
Rule: Adding 54.
Explanation:
Here, we need to add 54. If we check the difference between 162 and 108 we will get the difference as 54. So, we can see that in the given series, so 54 is added to the given numbers. So the rule is adding 54.
Question 9.
86, ___, 52, ___, 18, Rule: ___
Answer:
86, 69, 52, 35, 18, 1.
Rule: The difference between consecutive numbers is 17. 86, 69, 52, 35, 18, 1.
Explanation:
Here, we will subtraction 17 between the consecutive numbers.
Question 10.
425, ___, 339, ____, 253, ____ Rule: ___
Answer:
425, 382, 339, 296, 253, 210.
Rule: The difference between each pair of numbers is 43.
Explanation:
Here, the difference between each pair of the numbers is 43. So 425, 382, 339, 296, 253, 210.
Everyday Math Grade 4 Home Link 2.5 Answer Key
Prime and Composite Numbers
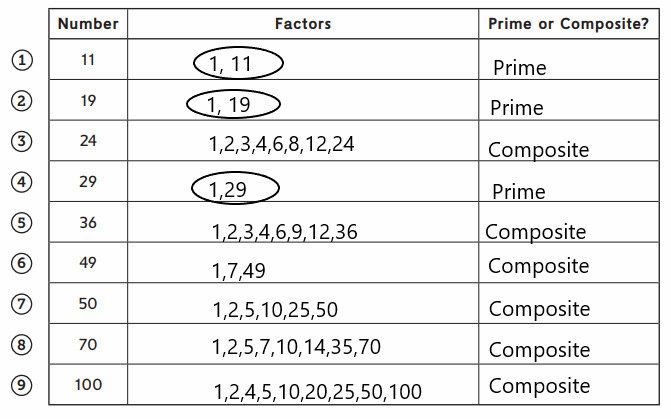
A prime number is a whole number that has exactly two different factors—1 and the number itself. A composite number is a whole number that has more than two different factors. For each number:
- List all of its factors.
- Write whether the number is prime or composite.
- Circle all of the factors that are prime numbers.
Practice
Solve.
Question 10.
841 + 527 = _____
Answer:
841 + 527 = 1,368.
Explanation:
The addition of the given two numbers 841 + 527 is 1,368.
Question 11.
____ = 3,263 + 5,059
Answer:
8,322 = 3,263 + 5,059
Explanation:
The addition of the given two numbers 3,263 + 5,059 is 8,322.
Question 12.
7,461 + 2,398 = _____
Answer:
7,461 + 2,398 = 9,859
Explanation:
The addition of the given two numbers 7,461 + 2,398 is 9,859.
Question 13.
___ = 4,172 – 3,236
Answer:
936 = 4,172 – 3,236
Explanation:
The difference between the given numbers 4,172 – 3,236 is 936.
Question 14.
8,158 = 5,071 + __
Answer:
The missing number is 3,087.
Explanation:
Let the missing number be x and we will replace the missing number with x, then 8,158 = 5,071 + x. So x is
x = 8,158 – 5,071
= 3,087.
Question 15.
3,742 – 3,349 = ___
Answer:
3,742 – 3,349 = 393.
Explanation:
The difference between the given numbers 3,742 – 3,349 is 393.
Everyday Math Grade 4 Home Link 2.6 Answer Key
Using Multiplication
Home Market sells 3 grapefruits for $2.
Question 1.
Darius spent $6 on grapefruits. How many did he buy? Use words, numbers, or diagrams to show your reasoning.
Answer:
Darius bought 9 grapefruits.
Explanation:
As Darius spent $6 on grapefruits, here home market sells 3 grapefruits for $2. So the number of grapefruits did Darius bought for $6 is 3 + 3 + 3 which is 9. So Darius bought 9 grapefruits.
Question 2.
Jana bought 15 grapefruits. How much did she spend? Use words, numbers, or diagrams to show your reasoning.
Answer:
Jana spends $10.
Explanation:
As Jana bought 15 grapefruits. here home market sells 3 grapefruits for $2. So the number of grapefruits did Darius bought for $6 is 2 + 2 + 2 + 2 + 2 which is 10. So Jana spends $10.
Question 3.
On the back of this page, write a multiplication number story about buying grapefruits at Home Market. Show how to solve your number story.
Answer:
Explanation:
Practice
Write these numbers using words.
Question 4.
12,309 _________________
Answer:
Twelve thousand three hundred and nine.
Explanation:
I have written the given numbers using words which is Twelve thousand three hundred and nine.
Question 5.
30,041 _________
Answer:
Thirty Thousand and forty-one.
Explanation:
I have written the given numbers using words which is Thirty Thousand and forty-one.
Question 6.
600,780 _________
Answer:
Six hundred thousand seven hundred eighty.
Explanation:
I have written the given numbers using words which is Six hundred thousand seven hundred eighty.
Question 7.
9,090,506 ________
Answer:
Ninety Lakh Ninety Thousand Five hundred Six.
Explanation:
I have written the given numbers using words which is Ninety Lakh Ninety Thousand Five hundred Six.
Everyday Math Grade 4 Home Link 2.6 Answer Key
Converting Units of Time
Use the measurement scales to fill in the tables and answer the questions.
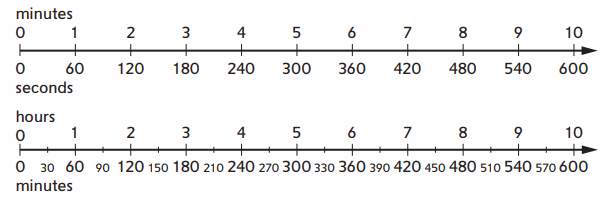
Question 1.
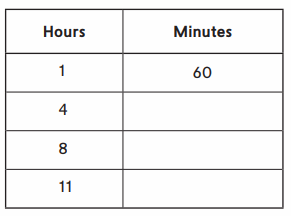
Answer:
Filled the table with minutes for the given hours using the measurement scales.
Explanation:
Here, we have filled the table with minutes for the given hours using the measurement scales.

Question 2.

Answer:
Filled the table with minutes for the given hours using the measurement scales.
Explanation:
Here, we have filled the table with seconds for the given minutes using the measurement scales.
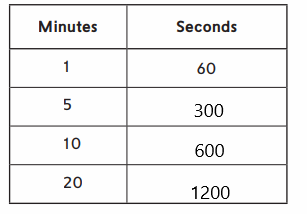
Question 3.
Zac worked on his spelling for 9 minutes last night and 8 minutes this afternoon. How many seconds did he work? Answer: seconds
Answer:
Zac worked 1,020 seconds.
Explanation:
Here, Zac worked on his spelling for 9 minutes last night and 8 minutes this afternoon, so the total number of minutes did Zac worked is 9 + 8 which is 17 minutes. Now we will convert minutes to seconds 17 × 60 which is 1,020 seconds. So Zac worked 1,020 seconds.
questions 4.
Eton’s baby sister took a nap for 2 hours and 22 minutes yesterday and 1 hour and 35 minutes today. How many more minutes did she sleep yesterday than today?
Answer: ___ minutes
Answer:
Eton’s baby sister took a nap yesterday then today is 47 minutes.
Explanation:
Here, Eton’s baby sister took a nap for 2 hours and 22 minutes yesterday, so the total number of minutes 120 + 22 which is 142 minutes. And 1 hour and 35 minutes today, so the total number of minutes 60 + 35 is 95 minutes. And the total number of minutes did Eton’s baby sister took a nap yesterday then today is 142 – 95 = 47 minutes.
Try This
Question 5.
How many seconds did Eton’s baby sister sleep all together?
Answer: ___ seconds
Answer:
The total number of seconds did Eton’s sister sleeps is 14,220 seconds.
Explanation:
Eton’s baby sister sleeps all together 142 + 95 which is 237 minutes and we need to convert minutes to seconds 237 × 60 = 14,220 seconds. So the total number of seconds did Eton’s sister sleeps is 14,220 seconds.
Practice
Question 6.
945 + 1,055 = ___
Answer:
945 + 1,055 = 2000
Explanation:
Add the two given numbers to get the resultant sum. Hence the answer is 2000.
Question 7.
2,953 + 4,471 = ___
Answer:
2,953 + 4,471 = 7424
Explanation:
Add the two given numbers to get the resultant sum. Hence the answer is 7424.
Question 8.
4,552 + 4,548 = ___
Answer:
4,552 + 4,548 = 9100
Explanation:
Add the two given numbers to get the resultant sum. Hence the answer is 9100.
Question 9.
3,649 + 3,649 = ___
Answer:
3,649 + 3,649 = 7298
Explanation:
Add the two given numbers to get the resultant sum. Hence the answer is 7298.
Everyday Math Grade 4 Home Link 2.8 Answer Key
Multiplicative Comparisons
Family Note In this lesson students used comparison statements and equations to represent situations in which one quantity is a number of times as much as another quantity. For example: José saved $5 over the summer. His sister saved 3 times as much. How much money did José’s sister save? In this number story students compare the amount of money José saved to the amount his sister saved. Students write the equation 3 ∗ 5 = 15 to represent this comparison and solve the problem:
José’s sister saved $15. Because these comparison statements and equations involve multiplication, they are called multiplicative comparisons.
Complete the problems below. Write an equation with a letter for the unknown and solve.
Question 1.
What number is 7 times as much as 9?
Equation with unknown:
Answer: ___
n = 7 × 9
63
Explanation:
The number which is 7 times as much as 9 is 63 and the equation is 7 × 9 which is 63.
Question 2.
What number is 5 times as much as 6?
Equation with unknown:
Answer: ___
n = 5 * 6
30
Explanation:
The number which is 5 times as much as 6 is 30 and the equation is 5 × 6 which is 30.
Question 3.
32 is 4 times as much as what number?
a. Equation with unknown: ___
b. Answer: ___
Answer:
n = 32 * 4
128
Explanation:
The number which is 32 times as much as 4 is 128 and the equation is 32 × 4 which is 128.
Question 4.
Write an equation to represent this situation and solve.
Ameer worked 3 times as many hours as Simi each week during the summer.
If Simi worked 10 hours each week, how many hours did Ameer work each week?
a. Equation with unknown: ____
Answer:
The number of hours did Ameer work each week is 30 hours.
Explanation:
Here, Ameer worked 3 times as many hours as Simi each week during the summer and Simi worked 10 hours each week. So the number of hours did Ameer work each week 3 × 10 which is 30 hours. So the number of hours did Ameer work each week is 30 hours.
Practice
Question 5.
7,482 – 7,083 = ___
Answer:
7,482 – 7,083 = 399
Explanation:
By subtracting the given numbers 7,482 – 7,083 the answer we get is 399.
Question 6.
7,702 – 3,581 = ___
Answer:
7,702 – 3,581 = 4121
Explanation:
By subtracting the given numbers 7,702 – 3,581 the answer we get is 4121.
Question 7.
5,201 – 3,052 = ___
Answer:
5,201 – 3,052 = 2149
Explanation:
By subtracting the given numbers 5,201 – 3,052 the answer we get is 2149.
Question .8
8,002 – 5,403 = ____
Answer:
8,002 – 5,403 = 2599
Explanation:
By subtracting the given numbers 8,002 – 5,403 the answer we get is 2599.
Everyday Math Grade 4 Home Link 2.9 Answer Key
Solving Multiplicative Comparison Number Stories
Make a diagram or drawing and write an equation to represent the situation. Then find the answer.
Question 1.
Judith collected 9 marbles. Swen has 6 times as many. How many marbles does Swen have?
Diagram or drawing:
Equation with unknown: ____
Answer:
54 marbles
Explanation:
Here the Swen has 54 marbles. As Judith collected 9 marbles and Swen has 6 times as many as Judith it means the Swen has 9 * 6 = 54 marbles.
Question 2.
Sol ran 4 times as many minutes as Jerry. Jerry ran 12 minutes. How many minutes did Sol run?
Diagram or drawing:
Equation with unknown: ____
Answer:
48 minutes
Explanation:
Here, Sol ran 4 times as many minutes as Jerry and Jerry ran 12 minutes. So the number of minutes did Sol ran 12 × 4 which 48 minutes.
Insert quantities into the number story. Make a diagram and write an equation to represent the story.
Question 3.
Lola picked apples. Eilene picked apples. Eilene picked times as many apples as Lola.
Diagram or drawing:
Equation with unknown: _____
Answer: ___ apples
Practice
Write these numbers in expanded form.
Question 4.
3,830 _________
Answer:
3000 + 800 + 30
Question 5.
56,037 ________
Answer:
50,000 + 6000 + 30 + 7
Question 6.
800,700 __
Answer:
800000 + 700
Question 7.
716,305 _____
Answer:
700,000 + 10,000 + 6000 + 300 + 5
Everyday Math Grade 4 Home Link 2.10 Answer Key
Identifying Triangles
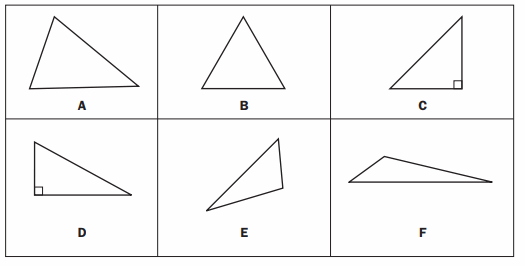
Write the letter or letters that match each statement.
Question 1.
Has perpendicular line segments
Answer:
C, D
Explanation:
The perpendicular line segments in the given question are C, D
Question 2.
Has an obtuse angle
Answer:
E, F
Explanation:
E and F are the triangles which are obtuse angle.
Question 3.
Has right angles
Answer:
C, D
Explanation:
C and D are the right angles.
Question 4.
Has acute angles
Answer:
A, B
Explanation:
A and B are the acute angles given in the question.
Question 5.
Has more than one kind of angle
Answer:
C, D, E, F
Explanation:
C, D, E, and F are the one kind of angle that is given in the question.
Question 6.
Has only one kind of angle
Answer:
A, B
Explanation:
A and B are the only kind of angle.
Question 7.
Does NOT have any right angles
Answer:
A, B, E, F
Explanation:
A, B, E, and F do not have any right angles in the given question.
Question 8.
Is a right triangle
Answer:
C, D
Explanation:
C and D is the right triangle in the given question.
Practice
Question 9.
List all the factors of 12.
Answer:
1, 2, 3, 4, 6, 12
Explanation:
The factors of 12 are 1, 2, 3, 4, 6, 12 because each of those divides 12 without leaving a remainder.
Question 10.
Name the next 4 multiples of 7. 35, _____, _____, ___, ____
Answer:
42, 49, 56, 63.
Explanation:
The next 4 multiples of 7 are 42, 49, 56, 63.
Everyday Math Grade 4 Home Link 2.11 Answer Key
Drawing Quadrilaterals
Question 1.
A parallelogram is a quadrilateral that has 2 pairs of parallel sides. Draw a parallelogram.

Answer:
I have drawn a parallelogram that has 2 pairs of parallel sides.
Explanation:
As asked in the question I have drawn a parallelogram below.
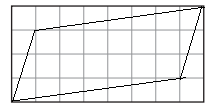
Question 2.
Answer each question, drawing pictures on the back of this page to help you.
a. Can a parallelogram have right angles? Explain.
b. Could a quadrilateral have 4 obtuse angles? Explain.
c. Name a quadrilateral that has at least 1 pair of parallel sides.
Answer:
a.
b. No, all the four angles of a quadrilateral cannot be obtuse. As the sum of the angles of a quadrilateral is 360∘, they may have a maximum of three obtuse angles.
c. Trapezoids
Trapezoids have only one pair of parallel sides.
Draw a quadrilateral that has at least 1 right angle.
Answer:
Question 4.
Draw a quadrilateral that has 2 separate pairs of equal length sides but is NOT a parallelogram.
This is called a ____.
Practice
Question 5.
5 ∗ 30 = ___
Answer:
150
Explanation:
By multiplying the given numbers the answer we get is 150.
Question 6.
__ = 40 ∗ 3
Answer:
120
Explanation:
By multiplying the given numbers the answer we get is 120.
Question 7.
___ = 80 ∗ 6
Answer:
480
Explanation:
By multiplying the given numbers the answer we get is 480.
Question 8.
6 ∗ 70 = ____
Answer:
420
Explanation:
By multiplying the given numbers the answer we get is 420.
Everyday Math Grade 4 Home Link 2.12 Answer Key
Drawing Lines of Symmetry
Question 1.
Draw the other half of each picture to make it symmetrical. Use a straightedge to form the line of symmetry.

Answer:
Question 2.
Draw a line of symmetry for each figure.
Answer:
Question 3.
List four items in your home that are symmetric. Pick one item and draw it below, including at least one line of symmetry.
Item: __ Item: ___ Drawing:
Item: __ Item: ___
Practice
Question 4.
___ = 2,767 + 3,254
Answer:
6021
Explanation:
Add the two given numbers to get the resultant sum. Hence the answer is 6021.
Question 5.
193 + 6,978 = ___
Answer:
7171
Explanation:
Add the two given numbers to get the resultant sum. Hence the answer is 7171.
Question 6.
7,652 − 5,388 = ___
Answer:
5674
Explanation:
By subtracting the given numbers the answer we get is 5674.
Question 7.
___ = 4,273 − 1,678
Answer:
2595
Explanation:
By subtracting the given numbers the answer we get is 2595.
Everyday Math Grade 4 Home Link 2.13 Answer Key
Identifying Patterns
Question 1.
Complete.
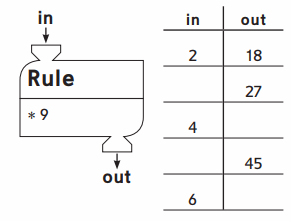
What patterns do you see?
Answer:
The pattern is multiples of 9.
Explanation:
The pattern is multiples of 9 in which 2 is in and 18 is out and that series continuous till the number 6.

Question 2.
Complete.
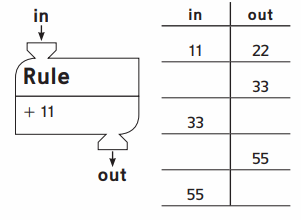
What patterns do you see?
Answer:
The pattern is adding 11.
Explanation:
The pattern is adding 11 in which 11 is in and 22 is out and that series continuous till the number 55.
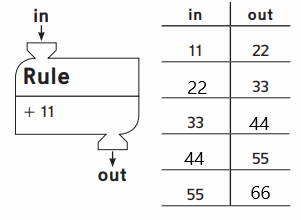
Question 3.
Study the pattern 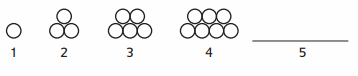
a. Draw the next step in the pattern. What patterns do you notice?
b. How many circles will be in the 6th step? __ In the 10thstep? ___
c. How did you figure out how many circles will be in the 10th step?
Answer:
a. In this question the number of circles is odd and increases by 2 every time.
Explanation:
I have drawn the next step in the pattern below.
b. 11; 19
Explanation:
There will be 11 circles in the 6th step. And 19 circles in the 10th step.
c. In this, each step is the next odd number so I skip counted from 1 by 2 until I got to the 10th step.
Explanation:
We can figure it out by observing each step given in the pattern. As in each step, the next one is an odd number so we can skip counted from 1 by 2 until we got to the 10th step.
Practice
Question 4.
800,000 + 90 = ___
Answer:
800,090
Explanation:
Add the two given numbers to get the resultant sum. Hence the answer is 800,090.
Question 5.
200,000 + 50,000 + 4 = ___
Answer:
250,004
Explanation:
Add the two given numbers to get the resultant sum. Hence the answer is 250,004.