Engage NY Eureka Math Precalculus Module 5 Lesson 14 Answer Key
Eureka Math Precalculus Module 5 Lesson 14 Exercise Answer Key
Exercises 1–3
Exercise 1.
At first glance of the probability distributions of the three games, without performing any calculations, which do you think might be the best choice and why?
Answer:
Answers will vary. Sample response: I think the spinning wheel might be the best choice because the probabilities are relatively high for winning 10 and 100 tickets.
Exercise 2.
Perform necessary calculations to determine which game to recommend to the child. Explain your choice in terms of both tickets and price. Is this the result you anticipated?

Answer:
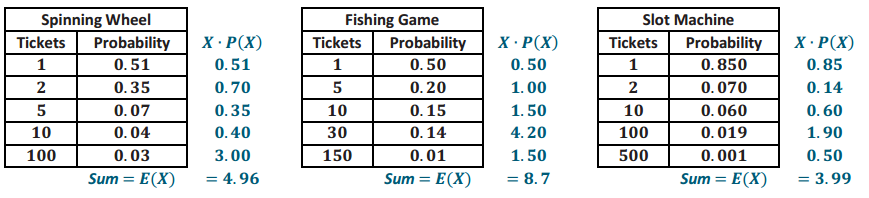
The fishing game would be the best game to play because, on average, the child will earn about 9 tickets for each play—but for the spinning wheel and slot machine games, she will only win about 5 or 4 tickets (respectively, on average) for each play.
The cost of the prize, if won by playing the fishing game, will average \(\frac{1000}{8.7}\)∙$0.50≈$57.47. If the spinning wheel or slot machine game is played, the average cost of the prize becomes \(\frac{1000}{4.96}\)∙$0.50≈$100.81 or
\(\frac{1000}{3.99}\)∙$0.50≈$125.31, respectively.
Answers about prediction will vary.
Exercise 3.
The child states that she would like to play the slot machine game because it offers a chance of winning 500 tickets per game, and that means she might only have to play twice to reach her goal, and none of the other games offer that possibility. Using both the information from the distributions above and your expected value calculations, explain to her why this might not be the best strategy.
Answer:
While the child is correct in her statement, the chances of earning 500 tickets with 1 play at the slot machine are very small. The event would happen in the long run only 1 out of 1,000 tries. The chances of earning 1,000 tickets in only 2 tries is very small (probability = 0.001∙0 .001 = 0.000 001 = \(\frac{1}{1000000}\) or 1 in 1 million). Given the rare chance of a high payout and the high chance of a low payout, the slot machine is not the way to go.
With the fishing game, she will earn about 9 tickets on average for each play—but for the spinning wheel and slot machine games, she will earn about half that many tickets on average with each play. That means that she may have to spend nearly twice the amount of money for the same expected number of tickets.
Exercise 4.
The company can market and maintain only one of the two policy types, and some people in the company feel it should market Plan B since it earns the higher premium from the customer and has the lower claim payout amount. Assume that the cost of required resources for the two types of policies is the same (for the advertising, selling, or maintaining of the policies) and that the same number of policies would be sold for either Plan A or Plan B. In terms of earning the most money for the insurance company, do you agree with the Plan B decision? Explain your decision.
Answer:

The Plan A policy would be better for the company as it has the higher expected value (and it is assumed that the same number of policies would be sold regardless of the plan). This means the company will earn more on average for every Plan A policy sold than it would for every Plan B policy sold—specifically, $20.65 more per policy sold on average. This difference will really add up as more and more policies are sold. So, even though Plan B has a higher premium and a lower payout, a payout is much more likely to occur with Plan B, making it the less attractive option.
Eureka Math Precalculus Module 5 Lesson 14 Problem Set Answer Key
Question 1.
In the previous lesson, a duck pond game was described with the following payout distribution to its players:
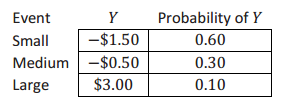
where Y represents the net amount that a player won (or lost) playing the duck game one time.
This led to a situation where the people running the game could expect to gain $0.75 on average per attempt.
Someone is considering changing the probability distribution as follows:
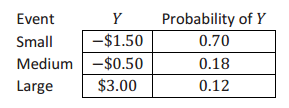
Will this adjustment favor the players, favor the game’s organizers, or will it make no difference at all in terms of the amount the organization can expect to gain on average per attempt?
Answer:
The expected value for the adjusted distribution:
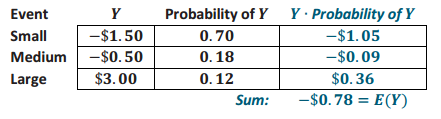
So, the new distribution will favor the game’s organizers. On average, the organizers will earn an additional $0.03 for every game played.
Question 2.
In the previous lesson’s Problem Set, you were asked to make a model of a spinning wheel with a point distribution as follows:
- You gain 2 points 50% of the time.
- You lose 3 points 25% of the time.
- You neither gain nor lose any points 25% of the time.
When X represents the number of points earned in a given spin, E(X) = 0.25 points.
Suppose you change the probabilities by “moving” 10% of the distribution as follows:
- You gain 2 points 60% of the time.
- You lose 3 points 15% of the time.
- You neither gain nor lose any points 25% of the time.
a. Without performing any calculations, make a guess as to whether or not this new distribution will lead to a player needing a fewer number of attempts than before on average to attain 5 or more points. Explain your reasoning.
Answer:
Since the chance of winning 2 points is higher, the chance of losing 3 points is lower, and the chance of earning 0 points is unchanged, that probably means that a person can reach 5 points more quickly than before.
b. Determine the expected value of points earned from 1 game based on this new distribution. Based on your computation, how many spins on average do you think it might take to reach 5 points?
Answer:
E(X) = 2∙0.60 + ( – 3)∙0.15 + 0∙0.25 = 0.75
The expected value tripled. Now it is expected to only take \(\frac{5}{0.75}\) = 6.67 (about 7) spins on average to reach 5 points.
c. Does this value from part (b) support your guess in part (a)? (Remember that with the original distribution and its expected value of 0.25 points per play, it would have taken 20 spins on average to reach 5 points.)
Answer:
Yes. The new distribution will only require 6.67 spins on average to reach 5 points. That is far fewer than the previous expected number of spins (20) needed on average to reach 5 points. This is in line with our conjecture back in part (a) that a person would be able to reach 5 points more quickly than before.
Question 3.
You decide to invest $1,000.00 in the stock market. After researching, you estimate the following probabilities:
- Stock A has a 73% chance of earning a 20% profit in 1 year, an 11% chance of earning no profit, and a 16% chance of being worthless.
- Stock B has a 54% chance of earning a 75% profit in 1 year, a 23% chance of earning no profit, and a 23% chance of being worthless.
a. At first glance, which seems to be the most appealing?
Answer:
Answers vary. Sample response: Stock A seems more appealing because there are lower probabilities of making no profit and losing the entire $1,000.00 investment.
b. Which stock should you decide to invest in and why? Is this what you predicted?
Answer:
Let X represent the value of the investment in Stock A after 1 year.
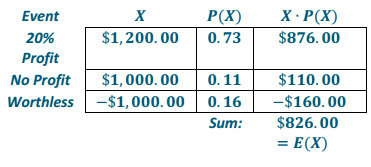
Let Yrepresent the value of the investment in Stock B after 1 year.

I should invest in Stock B because the total expected value of my investment is $945.00, whereas Stock B is only expected to yield $826.00. Stock B is riskier than Stock A, but the expected value is greater.
Question 4.
The clock is winding down in the fourth quarter of the basketball game. The scores are close. It is still anyone’s game. As the team’s coach, you need to quickly decide which player to put on the court to help ensure your team’s success. Luckily, you have the historical data for Player A and Player B in front of you.
- 80% of Player A’s shot attempts have been 2 – point field goals, and 60% of them have hit their marks.
The remaining shots have been 3 – point field goals, and 20% of them have hit their marks. - 85% of Player B’s shot attempts have been 2 – point field goals, and 62% of them have hit their marks.
The remaining shots have been 3 – point field goals, and 22% of them have hit their marks.
a. At first glance, whom would you put in and why?
Answer:
Answers vary.
b. Based on these statistics, which player might be more likely to help lead your team to victory and why?
Answer:
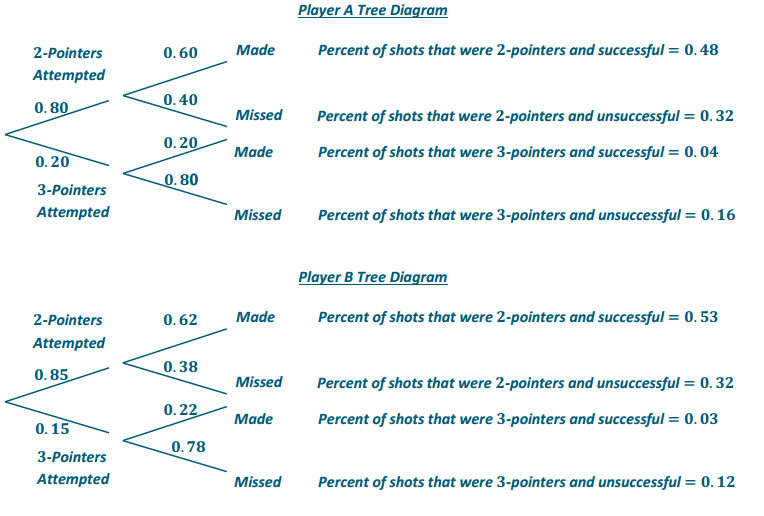
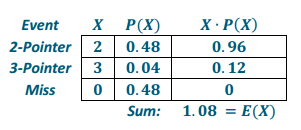
Let X represent Player A’s points per shot.
Let Y represent Player B’s points per shot.
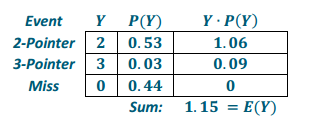
From the analysis, it appears as though Player B might be able to score slightly more points than Player A with 1.15 points per shot versus 1.08. However, both players have very close expected points per shot, so either would be a viable candidate.
Question 5.
Prior versions of College Board examinations (SAT, AP) awarded the test taker with 1 point for each correct answer and deducted \(\frac{1}{4}\) point for each incorrect answer. Current versions have eliminated the point deduction for incorrect responses (test takers are awarded 0 points).
The math section of the SAT contains 44 multiple – choice questions, with choices A–E. Suppose you answer all the questions but end up guessing on 8 questions. How might your math score look different on your score report using each point system? Explain your answer.
Answer:
Let X represent points per question with deduction.
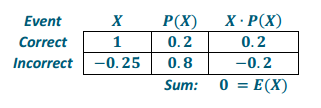
Let Y represent points per question without deduction.
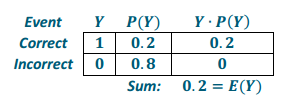
With the deduction system, a test taker would score an expected 0 points (0∙8) on the 8 guessed questions, while on the nondeduction system, a test taker would score an expected 1.6 points (0.2∙8) on the 8 guessed questions.
Eureka Math Precalculus Module 5 Lesson 14 Exit Ticket Answer Key
Question 1.
In the previous lesson, you examined the Maryland Lottery’s Pick 3 game where the chance of winning with a Front Pair bet is 0.01. (http://mdlottery.com/games/pick – 3/payouts)
In that game, a successful bet of $1.00 pays out $50.00 for a net gain to the player of $49.00.
Imagine that the state also offers a $1.00 scratch – off lottery game with the following net gain distribution:
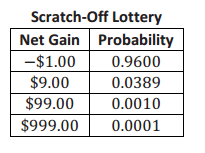
If you had a friend who wanted to spend $1.00 each day for several days on only 1 of these 2 lottery games, which game would you recommend? Explain.
Answer:
For the Maryland Lottery Pick 3, E(X) = 0 .99∙ – $1.00 + 0 .01∙$49.00 = – $0.99 + $0.49 = – $0.50
(determined in previous lesson).
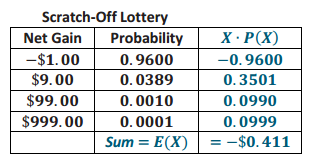
So, if a person was going to play a $1.00 game over and over again, he should play the scratch – off game as the player’s average loss per game is lower by about $0.09. (Note: Both games have negative expected values; placing the $1.00 in a bank savings account each day is a much better idea in terms of earning money.)