Eureka Math Precalculus Module 4 End of Module Assessment Answer Key

Engage NY Eureka Math Precalculus Module 4 End of Module Assessment Answer Key

Eureka Math Precalculus Module 4 End of Module Assessment Task Answer Key

Question 1.
a. In the following diagram, triangle XYZ has side lengths a, b, and c as shown. The angle α indicated is acute. Show that the area A of the triangle is given by A=\(\frac{1}{2}\) ab sin⁡(α).

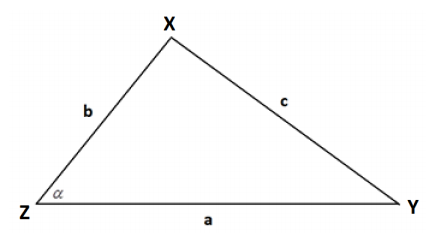
Answer:
Draw an altitude as shown. Call its length h.

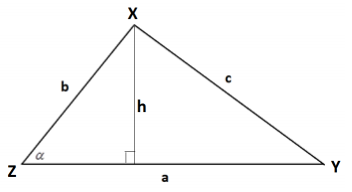
We have sin ⁡(α ) = \(\frac{h}{b}\) , so h = b sin ⁡(α) .
The area A of the triangle is given as “half base times height.” So
A = \(\frac{1}{2}\) × a × b sin ⁡(α ) = \(\frac{1}{2}\) ab sin ⁡(α ) .

b. In the following diagram, triangle PQR has side lengths p, q, and r as shown. The angle β indicated is obtuse. Show that the area A of the triangle is given by A=\(\frac{1}{2}\) pq sin⁡(β).

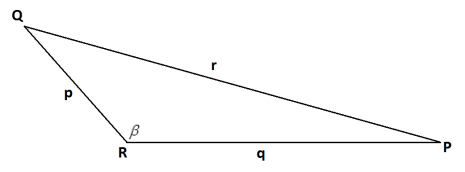
Answer:
Draw in an altitude as shown. Call its length h .

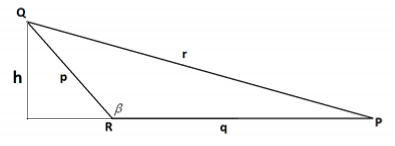
We have sin ⁡(π – β ) = \(\frac{h}{p}\), so h = p sin ⁡(π – β) . Since sin ⁡(π – β ) = sin ⁡(β) , this can be rewritten h = p sin ⁡(β) .
The area A of the triangle is thus \(\frac{1}{2}\) × q × p sin ⁡(β ) = \(\frac{1}{2}\) pq sin ⁡(β) .

c. To one decimal place, what is the area of the triangle with sides of lengths 10 cm, 17 cm, and 21 cm? Explain how you obtain your answer.
Answer:
Let θ be the measure of the angle between the sides of lengths 10 cm and 17 cm . By the law of cosines, we have 21² = 10² + 17² – 2 ∙ 10 ∙ 17 cos ⁡(θ) . This gives
cos ⁡(θ ) = \(\frac{52}{340}\) = \(\frac{13}{85}\), and so θ = cos^–1 (\(\frac{13}{85}\)) ≈ 1.42 radians.
\(\frac{1}{2}\) ∙ 10 ∙ 17 sin ⁡(θ ) ≈ 85 sin ⁡(1.42) ≈ 84.0
The area of the triangle is 84.0 square centimeters.

Question 2.
Triangle ABC with side lengths a, b, and c as shown is circumscribed by a circle with diameter d.

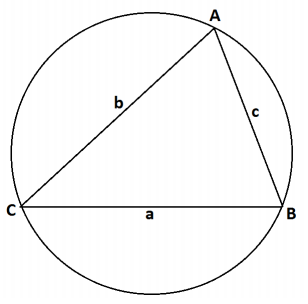
a. Show that \(\frac{a}{\sin (A)}\) =d.
Answer:
Consider the pointA’ on the circle with \(\overline{\mathrm{A}^{\prime} B}\) a diameter of the circle.

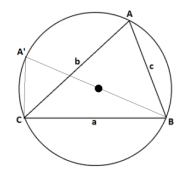
By Thales’ theorem (an inscribed angle that intercepts a semi-circle is a right angle),∠A’CB is a right angle. Thus,sin (A’ ) = \(\frac{a}{d}\).
But by the inscribed angle theorem (angles intercepting the same arc are congruent), the inscribed angle atA’ has the same measure as the inscribed angle atA . So,sin (A’ ) = sin ⁡(A) , and our equation readssin (A ) = \(\frac{a}{d}\). Rearranging gives \(\frac{a}{\sin (A)}\) = d .

b. The law of sines states that \(\frac{a}{\sin (A)}\)=\(\frac{b}{\sin (B)}\)=\(\frac{c}{\sin (C)}\) for any triangle ABC with side lengths a, b, and c (with the side of length a opposite vertex A, the side of length b opposite vertex B, and the side of length c opposite vertex C). Explain why the law of sines holds for all triangles.
Answer:
The relationship between a, sin(A), and d holds for any side of the triangle. So we also have \(\frac{b}{\sin (B)}\) = d and \(\frac{c}{\sin (C)}\) = d . This shows that \(\frac{a}{\sin (A)}\) = \(\frac{b}{\sin (B)}\) = \(\frac{c}{\sin (C)}\) for a triangle circumscribed by a circle.

As every triangle can be circumscribed by a circle, the law of sines,
\(\frac{a}{\sin (A)}\) = \(\frac{b}{\sin (B)}\) = \(\frac{c}{\sin (C)}\), thus holds for all triangles.

c. Prove that c²=a²+b²-2ab cos⁡(C) for the triangle shown in the original diagram.
Answer:

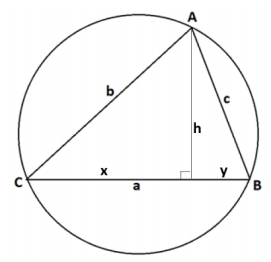
Draw an altitude as shown for the triangle, and identify the three lengths x , y , and h as shown.
Now x = b cos ⁡(C ),h = b sin ⁡(C) , and
y = a – x = a – b cos ⁡(C) .
Applying the Pythagorean theorem to the right triangle on the right, we have
y² + h² = c²
(a – b cos ⁡(C))² + (b sin ⁡(C))² = c²
a² – 2ab cos ⁡(C ) + b² cos² (C ) + b² sin² (C ) = c²
Using cos² (C ) + sin² (C ) = 1 this reads
a² – 2ab cos ⁡(C ) + b² = c²
or
c² = a² + b² – 2ab cos ⁡(C) .

Question 3.
Beatrice is standing 20 meters directly east of Ari, and Cece is standing 15 meters directly northeast of Beatrice.

a. To one decimal place, what is the distance between Ari and Cece?
Answer:
The following diagram depicts the situation described:

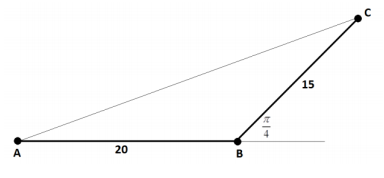
By the law of cosines
|AC |² = 20² + 15² – 2 ∙ 15 ∙ 20 ∙ cos ⁡(\(\frac{3\pi}{4}\))
|AC |² = 400 + 225 – 600 (– \(\frac{1}{\sqrt{2}}\))
|AC |² = 625 + 300 \(\sqrt{2}\)
|AC | = \(\sqrt{625+300 \sqrt{2}}\) ≈ 32.4
Thus, the distance between Ari and Cece is approximately 32.4 meters.

b. To one decimal place, what is the measure of the smallest angle in the triangle formed by Ari, Beatrice, and Cece?
Answer:
The angle of the smallest measure in a triangle lies opposite the shortest side of the triangle. Thus, we seek the measure of the angle at Ari’s position.
By the law of sines
\(\frac{\sin (A)}{15}=\frac{\sin \left(\frac{3 \pi}{4}\right)}{|A C|}\)
giving
sin ⁡(A ) = \(\frac{15}{\sqrt{2}|A C|}\) ≈ \(\frac{1.5}{\sqrt{2} \cdot 32.4}\) ≈ 0.33.
Thus, m ∠A ≈ sin^-1 (0.33 ) ≈ 0.33 radian. (This is about 19° .)

Question 4.
a. Is it possible to construct an inverse to the sine function if the domain of the sine function is restricted to the set of real values between \(\frac{\pi}{2}\) and \(\frac{3\pi}{2}\)? If so, what is the value of sin^-1 (\(\frac{1}{2}\)) for this inverse function? Explain how you reach your conclusions.
Answer:

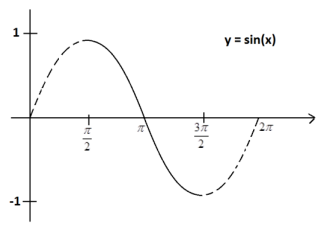
We see, when restricted to inputs between \(\frac{\pi}{2}\) and \(\frac{3\pi}{2}\), the graph of y = sin ⁡(x) is strictly decreasing.
Thus for each value between –1 and 1 , there is an input value x within this range for which sin ⁡(x) has this value. That is, there is indeed an inverse function for sine in this restricted domain.
We know that sin ⁡(\(\frac{\pi}{6}\)) = \(\frac{1}{2}\). So it follows that sin ⁡(π + \(\frac{\pi}{6}\)) = – \(\frac{1}{2}\). For our inverse function we have
sin^-1 (– \(\frac{1}{2}\)) = π + \(\frac{\pi}{6}\) = \(7\frac{\pi}{6}\) .

b. Is it possible to construct an inverse to the cosine function if the domain of the cosine function is restricted to the set of real values between \(\frac{\pi}{2}\) and \(\frac{3\pi}{2}\)? If so, what is the value of cos^-1 (\(\frac{1}{2}\)) for this inverse function? Explain how you reach your conclusions.
Answer:

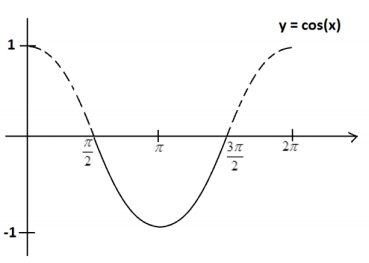
The value of the cosine function is neither strictly increasing nor strictly decreasing on that restricted domain.
There are distinct inputs from the restricted domain that give the same cosine values, and so it is not possible to construct an inverse to the cosine for this domain.

c. Is it possible to construct an inverse to the tangent function if the domain of the tangent function is restricted to the set of real values between \(\frac{\pi}{2}\) and \(\frac{3\pi}{2}\)? If so, what is the value of tan^-1 (-1) for this inverse function? Explain how you reach your conclusions.
Answer:
The graph of the tangent function is strictly increasing on the restricted domain:

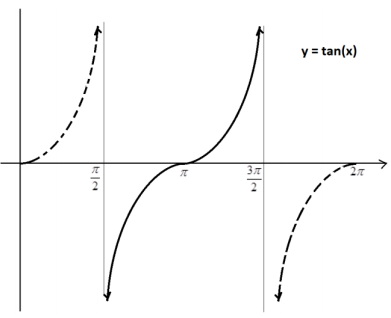
For each real number y , there is indeed a unique real number x in this restricted domain with tan ⁡(x ) = y . We can thus construct an inverse function.
We know that tan ⁡(\(\frac{\pi}{4}\) ) = 1 , and so we see that tan ⁡(π + \(\frac{\pi}{4}\)) = –1 . Thus for our inverse function, tan^–1 (–1 ) = \(\frac{5\pi}{4}\).

Question 5.
The diagram shows part of a rugby union football field. The goal line (marked) passes through two goal posts (marked as black circles) set 5.6 meters apart.

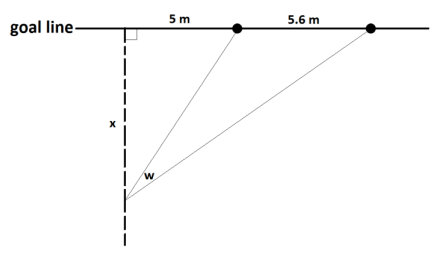
According to the rules of the game, an attempt at a conversion must be taken at a point on a line through the point of touchdown and perpendicular to the goal line. If a touchdown occurred 5 meters to one side of a goal post on the goal line, for example, the dashed line in the diagram indicates the line on which the conversion must be attempted.
Suppose the conversion is attempted at a distance of x meters from the goal line. Let w be the angle (measured in radians) indicated subtended by the goal posts.
a. Using inverse trigonometric functions, write an expression for w in terms of the distance x.
Answer:
Label the angle y as shown:

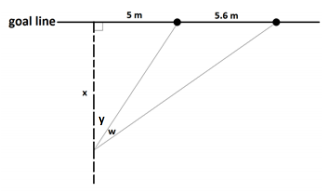
We have tan ⁡(y ) = \(\frac{5}{x}\) and tan ⁡(y + w ) = \(\frac{10.6}{x}\) and so
w = (y + w ) – y = tan^–1 (\(\frac{10.6}{x}\)) – tan^–1 (\(\frac{5}{x}\)).

b. Using a graphing calculator or mathematics software, sketch a copy of the graph of the angle measure w as a function of x on the axes below. Indicate on your sketch the value of x that maximizes w. What is that maximal angle measure? (Give all your answers to two decimal places.)

Answer:
We see

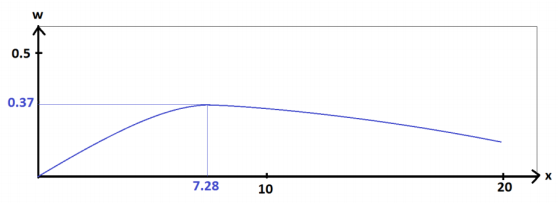
At x = 7.28 , the angle w has a measure of 0.37 radian. (This is about 21° .)

c. In the original diagram, we see that the angle of measure w is one of three angles in an obtuse triangle. To two decimal places, what is the measure of the obtuse angle in that triangle when w has its maximal possible measure?
Answer:
Label the obtuse angle a and the length L as shown.

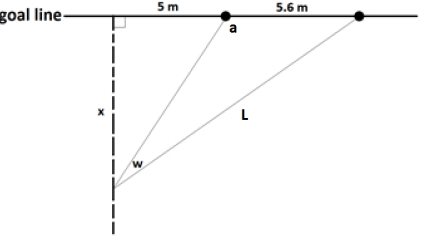
For x = 7.28 and w = 0.37 , we have
L = \(\sqrt{10.6^{2}+7.28^{2}}\) ≈ 12.86 , in meters.
By the law of sines,
\(\frac{\sin (a)}{L}=\frac{\sin (w)}{5.6}\)

So sin ⁡(a ) = \(\frac{L \sin (w)}{5.6}\) ≈ \(\frac{12.86 \times \sin (0.37)}{5.6}\) ≈ 0.83 .
Thus, a = sin^–1 (0.83 ) = 0.98 or π – 0.98 .

Since we are working with an obtuse angle, we must have a = π – 0.98 ≈ 2.16 radians. (This is about 124° .)

Question 6.
While riding her bicycle, Anu looks down for an instant to notice a reflector attached to the front wheel near its rim. As the bicycle moves, the wheel rotates and the position of the reflector relative to the frame of the bicycle changes. Consequently, the angle down from the horizontal that Anu needs to look in order to see the reflector changes with time.

Anu also notices the air valve on the rim of the front wheel tire and observes that the valve and the reflector mark off about one-sixth of the perimeter of the front wheel.

As Anu rides along a straight path, she knows that there will be a moment in time when the reflector, the valve, and her eye will be in line. She wonders what the angle between the horizontal from her eye and the line from her eye to the reflector passing through the valve is at this special moment.

She estimates that the reflector and the valve are each 1.5 feet from the center of the front wheel, that her eye is 6 feet away from the center of that wheel, and that the line between her eye and the wheel center is 45° down from the horizontal.

According to these estimates, what is the measure, to one decimal place in radians, of the angle Anu seeks?

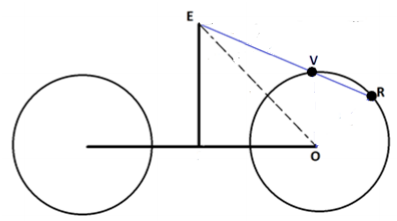
In this diagram, O represents the center of the front wheel, E the location of Anu’s eye, and R and V the positions of the reflector and valve, respectively, at the instant R, V, and E are collinear.
Answer:
The following is a schematic diagram of Anu on her bicycle. The point O is the center of the front wheel, the point E is the location of Anu’s eye, and the points R and V are the locations of the reflector and the valve, respectively, on the rim of the front wheel and the instant those two points and E are collinear. We have |EO| = 6 feet and
|OR | = |OV | = 1.5 feet, and we seek the measure of angle a shown.

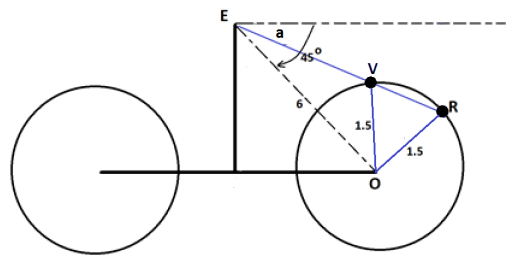
We are told that the length of the arc between V and R is one-sixth of the perimeter of the wheel. Thus m ∠VOR = \(\frac{1}{6}\) ∙ 2π = \(\frac{\pi}{3}\) radian. Consequently, m ∠EVO = \(\frac{2\pi}{3}\).

Looking at triangle EVO , the law of sines gives \(\frac{6}{\sin \left(\frac{2 \pi}{3}\right)}\) = \(\frac{1.5}{\sin (m \angle V E O)}\), and so sin ⁡(m∠VEO ) = \(\frac{\sin \left(\frac{2 \pi}{3}\right)}{4}\) =\(\frac{\sqrt{3}}{8}\). Thus, m ∠VEO = sin^–1 (\(\frac{\sqrt{3}}{8}\)) radians. Since ∠EVO is obtuse, ∠VEO is acute, and we must work with the value of sin^–1 (\(\frac{\sqrt{3}}{8}\)) that corresponds to the measure of an acute angle.

It follows that m ∠a = \(\frac{\pi}{3}\) – sin^–1 (\(\frac{\sqrt{3}}{8}\)) ≈ 0.6 radians (which is about 34° ).