Engage NY Eureka Math Precalculus Module 3 Lesson 21 Answer Key
Eureka Math Precalculus Module 3 Lesson 21 Exploratory Challenge/Exercise Answer Key
Exploratory Challenge/Exercises 1–14
By examining the amount of Carbon – 14 that remains in an organism after death, one can determine its age. The half – life of Carbon – 14 is 5, 730 years, meaning that the amount of Carbon – 14 present is reduced by a factor of \(\frac{1}{2}\) every 5, 730 years.
Exercise 1.
Complete the table.

Answer:

Let C be the function that represents the number of C – 14 atoms remaining per 1.0×108 C – 12 atoms t years after death.
Exercise 2.
What is C(11, 460)? What does it mean in this situation?
Answer:
C(11460) = 2500
Each time the years since death increase by 5, 730, you have to reduce the C – 14 atoms per 1.0×108 C – 12 atoms by a factor of \(\frac{1}{2}\). After the organism has been dead for 11, 460 years, the organism contains 2, 500 C – 14 atoms per 1.0×108 C – 12 atoms.
Exercise 3.
Estimate the number of C – 14 atoms per 1.0×108 C – 12 atoms you would expect to remain in an organism that died 10, 000 years ago.
Answer:
It would be slightly more than 2, 500 atoms, so approximately 3, 100.
Exercise 4.
What is C-1(625)? What does it represent in this situation?
Answer:
C-1(625) = 22, 920
This represents the number of years since death when there are 625 C – 14 atoms per
1.0×108 C – 12 atoms remaining in the sample.
Exercise 5.
Suppose the ratio of C – 14 to C – 12 atoms in a recently discovered woolly mammoth was found to be 0.000 001. Estimate how long ago this animal died.
Answer:
We need to write this as a ratio with a denominator equal to 1.0×108.
0.000 001 = 1.0×10 – 6 = \(\frac{1.0 \times 10^{2}}{1.0 \times 10^{8}}\)
So, if the number of C – 12 atoms is 1.0 × 108, then the number of C – 14 atoms would be 100. This animal would have died between 34, 000 and 40, 000 years ago.
Exercise 6.
Explain why the C-1(100) represents the answer to Exercise 5.
Answer:
C-1(100) means the value of x when C(x) = 100. We wanted the time when there would be 100 C – 14 atoms for every 1.0 × 108 C – 12 atoms.
Exercise 7.
What type of function best models the data in the table you created in Exercise 1? Explain your reasoning.
Answer:
Since the data is being multiplied by a constant factor each time the years increase by the same amount, this data would be modeled best by an exponential function.
Exercise 8.
Write a formula for C in terms of t. Explain the meaning of any parameters in your formula.
Answer:
C(t) = \(10000\left(\frac{1}{2}\right)^{\frac{t}{5730}}\)
The 10, 000 represents the number of C – 14 atoms per 1.0×108 C – 12 atoms present at the death of the organism. The 5, 730 and the \(\frac{1}{2}\) indicate that the amount is halved every 5, 730 years.
Exercise 9.
Graph the set of points (t, C(t)) from the table and the function C to verify that your formula is correct.
Answer:
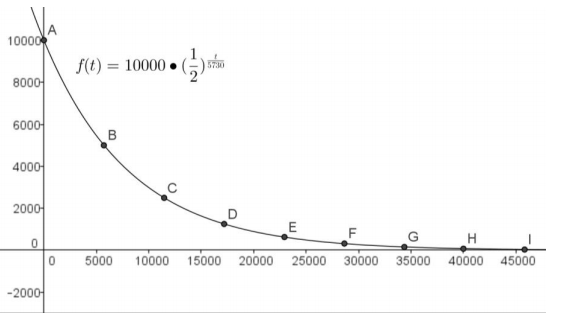
Exercise 10.
Graph the set of points (C(t), t) from the table. Draw a smooth curve connecting those points. What type of function would best model this data? Explain your reasoning.
Answer:
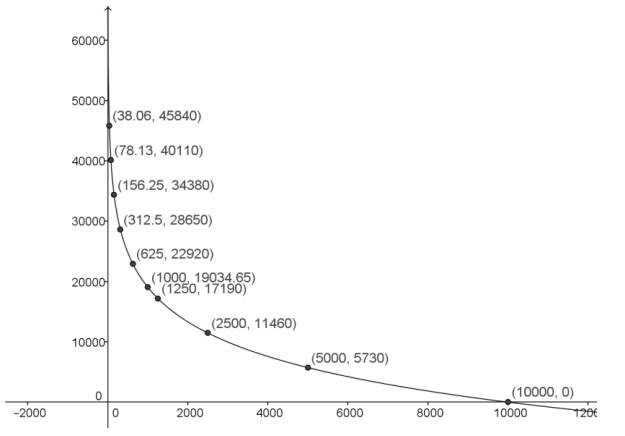
This data would best be modeled by a logarithmic function since the data points represent points on the graph of the inverse of an exponential function.
Exercise 11.
Write a formula that gives the years since death as a function of the amount of C – 14 remaining per 1.0×108 C – 12 atoms.
Answer:
Take the equation C(t) = 10000(\(\frac{1}{2}\)), and use the variables x and y in place of t and C(t). Find the inverse by exchanging the x and y variables and solving for y.
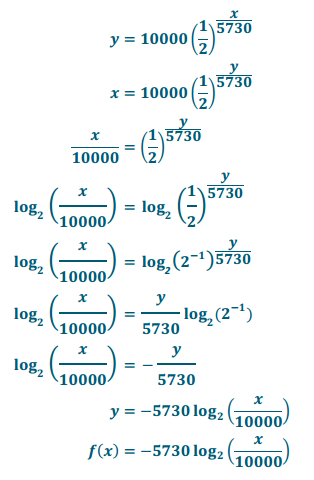
In this formula, x is the number of C – 14 atoms for every 1.0×108 C – 12 atoms, and f(x) is the time since death.
Exercise 12.
Use the formulas you have created to accurately calculate the following:
a. The amount of C – 14 atoms per 1.0×108 C – 12 atoms remaining in a sample after 10, 000 years
Answer:
y = \(10000\left(\frac{1}{2}\right)^{\frac{10000}{5730}}\)
C(10000) ≈ 2981
There are approximately 2, 981 C – 14 atoms per 1.0×108 C – 12 atoms in a sample that died 10, 000 years ago.
b. The years since death of a sample that contains 100 C – 14 atoms per 1.0×108 C – 12 atoms
Answer:
f(x) = – \(5730 \log _{2}\left(\frac{100}{10000}\right)\)
f(100) ≈ 38069
An organism containing 100 C – 14 atoms per 1.0×108 C – 12 atoms died 38, 069 years ago.
c. C(25, 000)
Answer:
y = \(10000\left(\frac{1}{2}\right)^{\frac{25000}{5730}}\)
C(25000) ≈ 486
After an organism has been dead for 25, 000 years, there are approximately 486 C – 14 atoms per
1.0×108 C – 12 atoms.
d. C-1(1, 000)
Answer:
f(x) = – \(5730 \log _{2}\left(\frac{1000}{10000}\right)\)
To find this amount, evaluate f(1000) ≈ 19035.
When there are 1, 000 C – 14 atoms per 1.0×108 C – 12 atoms, the organism has been dead for 19, 035 years.
Exercise 13.
A baby woolly mammoth that was discovered in 2007 died approximately 39, 000 years ago. How many C – 14 atoms per 1.0×108 C – 12 atoms would have been present in the tissues of this animal when it was discovered?
Answer:
Evaluate C(39000) ≈ 89 atoms of C – 14 per 10×108 atoms of C – 12.
Exercise 14.
A recently discovered woolly mammoth sample was found to have a red liquid believed to be blood inside when it was cut out of the ice. Suppose the amount of C – 14 in a sample of the creature’s blood contained 3, 000 atoms of C – 14 per 1.0×108 atoms of C – 12. How old was this woolly mammoth?
Answer:
Evaluate C-1(3000) ≈ 9953. The woolly mammoth died approximately 10, 000 years ago.
Exercises 15–18
Scientists can infer the age of fossils that are older than 50, 000 years by using similar dating techniques with other radioactive isotopes. Scientists use radioactive isotopes with half – lives even longer than Carbon – 14 to date the surrounding rock in which the fossil is embedded.
A general formula for the amount A of a radioactive isotope that remains after t years is A = \(A_{0}\left(\frac{1}{2}\right)^{\frac{t}{h}}\)
where A0 is the amount of radioactive substance present initially and h is the half – life of the radioactive substance.
Exercise 15.
Solve this equation for t to find a formula that infers the age of a fossil by dating the age of the surrounding rocks.
Answer:
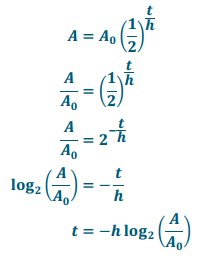
Exercise 16.
Let (x) = \(A_{0}\left(\frac{1}{2}\right)^{\frac{x}{h}}\). What is A-1(x)?
Answer:
A-1(x) = – h log2\(\left(\frac{x}{A_{0}}\right)\)
Exercise 17.
Verify that A and A-1are inverses by showing that A(A-1(x)) = x and A-1(A(x)) = x.
Answer:
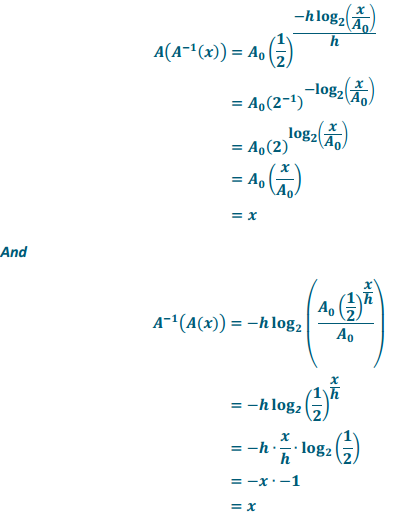
Exercise 18.
Explain why, when determining the age of organic materials, archaeologists and anthropologists would prefer to use the logarithmic function to relate the amount of a radioactive isotope present in a sample and the time since its death.
Answer:
Defining the years since death as a function of the amount of radioactive isotope makes more sense since archaeologists and anthropologists are trying to determine the number of years since the death of an organism from a sample. They know the amount of the radioactive isotope and can use that as an input into the formula to generate the number of years since its death.
Eureka Math Precalculus Module 3 Lesson 21 Problem Set Answer Key
Question 1.
A particular bank offers 6% interest per year compounded monthly. Timothy wishes to deposit $1, 000.
a. What is the interest rate per month?
Answer:
\(\frac{0.06}{12}\) = 0.005
b. Write a formula for the amount A Timothy has after n months.
Answer:
A = 1000(1.005)n
c. Write a formula for the number of months it takes Timothy to have A dollars.
Answer:
n = \(\frac{\ln \left(\frac{A}{1000}\right)}{\ln (1.005)}\)
d. Doubling – time is the amount of time it takes for an investment to double. What is the doubling – time of Timothy’s investment?
Answer:
n = \(\frac{\ln (2)}{\ln (1.005)}\)
≈ 138.98
It takes 139 months for Timothy’s investment to double.
e. In general, what is the doubling – time of an investment with an interest rate of r/12 per month?
Answer:
n = \(\frac{\ln (2)}{\ln \left(1 + \frac{r}{12}\right)}\)
Question 2.
A study done from 1950 through 2000 estimated that the world population increased on average by 1.77% each year. In 1950, the world population was 2, 519 million.
a. Write a formula for the world population t years after 1950. Use p to represent the world population.
Answer:
p = 2519(1.0177)t
b. Write a formula for the number of years it takes to reach a population of p.
Answer:
t = \(\frac{\ln \left(\frac{p}{2519}\right)}{\ln (1.0177)}\)
c. Use your equation in part (b) to find when the model predicts that the world population is 10 billion.
Answer:
t = \(\frac{\ln \left(\frac{10000}{2519}\right)}{\ln (1.0177)}\)
≈ 78.581
According to the model, it takes about \(78 \frac{1}{2}\) years from 1950 for the world population to reach 10 billion; this would be in 2028.
Question 3.
Consider the case of a bank offering r (given as a decimal) interest per year compounded monthly, if you
deposit $P.
a. What is the interest rate per month?
Answer:
\(\frac{r}{12}\)
b. Write a formula for the amount A you have after n months.
Answer:
A = \(A = P\left(1 + \frac{r}{12}\right)^{n}\)
c. Write a formula for the number of months it takes to have A dollars.
Answer:
\(\ln \left(\frac{A}{P}\right) = n \cdot \ln \left(1 + \frac{r}{12}\right)\)
\(n = \frac{\ln \left(\frac{A}{P}\right)}{\ln \left(1 + \frac{r}{12}\right)}\)
d. What is the doubling – time of an investment earning 7% interest per year, compounded monthly? Round up to the next month.
Answer:
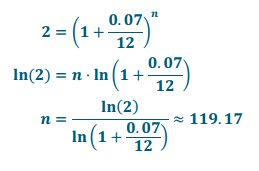
It would take 120 months or 10 years in order to double an investment earning 7% interest per year, compounded monthly.
Question 4.
A half – life is the amount of time it takes for a radioactive substance to decay by half. In general, we can use the equation A = P(\(\frac{1}{2}\))t for the amount of the substance remaining after t half – lives.
a. What does P represent in this context?
Answer:
The initial amount of the radioactive substance
b. If a half – life is 20 hours, rewrite the equation to give the amount after h hours.
Answer:
\(t = \frac{h}{20}\)
\(A = P\left(\frac{1}{2}\right)^{\frac{h}{20}}\)
c. Use the natural logarithm to express the original equation as having base e.
Answer:
\(A = P e^{\ln \left(\frac{1}{2}\right) t}\)
d. The formula you wrote in part (c) is frequently referred to as the “Pert” formula, that is, Pert. Analyze the value you have in place for r in part (c). What do you notice? In general, what do you think r represents?
Answer:
r = \(\ln \left(\frac{1}{2}\right)\)
It seems like the r value always represents the natural logarithm of the growth rate per t. If t is a number of half – lives, then r is the natural logarithm of \(\frac{1}{2}\).
e. Jess claims that any exponential function can be written with base e; is she correct? Explain why.
Answer:
She is correct. No matter what the original rate is, say b, we can always rewrite the rate as eln(b), so e is always a possible base for an exponential function. Similarly, we could always rewrite logarithms in terms of the natural logarithm.
Question 5.
If caffeine reduces by about 10% per hour, how many hours h does it take for the amount of caffeine in a body to reduce by half (round up to the next hour)?
Answer:
\(\frac{1}{2} = 1 \cdot(0.9)^{h}\)
h = \(\frac{\ln \left(\frac{1}{2}\right)}{\ln (0.9)}\)
≈ 6.5788
It takes about 7 hours for the caffeine to reduce by half.
Question 6.
Iodine – 123 has a half – life of about 13 hours, emits gamma – radiation, and is readily absorbed by the thyroid. Because of these facts, it is regularly used in nuclear imaging.
a. Write a formula that gives you the percent p of iodine – 123 left after t half – lives.
Answer:
A = \(P\left(\frac{1}{2}\right)^{t}\)
\(\frac{A}{P} = \left(\frac{1}{2}\right)^{t}\)
p = \(\left(\frac{1}{2}\right)^{t}\)
b. What is the decay rate per hour of iodine – 123? Approximate to the nearest millionth.
Answer:
t = \(\frac{h}{13}\)
p = \(\left(\frac{1}{2}\right)^{\frac{h}{13}}\)
p = \(\left.\left(\frac{1}{2}\right)^{1 / 13}\right)^{h}\)
p ≈ (0.948 078)h
Iodine – 123 decays by about 0.051 922 per hour, or 5.1922%.
Question 7.
Use your result to part (b). How many hours h would it take for you to have less than 1% of an initial dose of iodine – 123 in your system? Round your answer to the nearest tenth of an hour.
Answer:
0.01 = (0.948 078)h
h = \(\frac{\ln (0.01)}{\ln (0.948078)}\)
≈ 86.4
It would take approximately 86.4 hours for you to have less than 1% of an initial does of iodine – 123 in your system.
Question 7.
An object heated to a temperature of 50°C is placed in a room with a constant temperature of 10°C to cool down. The object’s temperature T after t minutes can be given by the function T(t) = 10 + 40e – 0.023 105t.
a. How long does it take for the object to cool down to 30°C?
Answer:
30 = 10 + 40e – 0.023 105t
\(\frac{1}{2} = e^{ – 0.023105 t}\)
t = \(\frac{\ln \left(\frac{1}{2}\right)}{ – 0.023105}\) ≈ 29.9999
About 30 minutes
b. Does it take longer for the object to cool from 50°C to 30°C or from 30°C to 10.1°C?
Answer:
Since it is an exponential decay function, it takes longer for the object to cool from 30°C to 10.1°C than it takes for the object to cool from 50°C to 30°C. The function levels off as it approaches 10°C, so it takes progressively longer. It would take an additional 70 minutes to cool down to 10.1°C after getting to 30°C.
c. Will the object ever be 10°C if kept in this room?
Answer:
It will effectively be 10°C eventually, but mathematically it will never get there. After 400 minutes, the temperature will be about 10.0001°C.
d. What is the domain of T-1? What does this represent?
Answer:
The domain of the inverse represents the possible temperatures that the object could be, so (10, 50].
Question 8.
The percent of usage of the word judgment in books can be modeled with an exponential decay curve. Let P be the percent as a function of x, and let x be the number of years after 1900; then, P(x) = 0.022 046 5 ⋅ e– 0.007 994 1x.
a. According to the model, in what year was the usage 0.1% of books?
Answer:
\(P^{ – 1}(x) = \frac{\ln \left(\frac{x}{0.0220465}\right)}{ – 0.0079951}\)
According to the inverse of the model, we get a value of – 189, which corresponds to the year 1711.
b. When does the usage of the word judgment drop below 0.001% of books? This model was made with data from 1950 to 2005. Do you believe your answer is accurate? Explain.
Answer:
We get a value of 387, which corresponds to the year 2, 287. It is unlikely that the model would hold up well in either part (a) or part (b) because these years are so far in the past and future.
c. Find P-1. What does the domain represent? What does the range represent?
Answer:
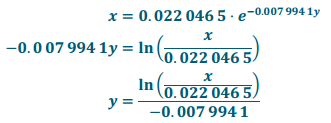
The domain is the percent of books containing the word “judgment” while the range is the number of years after 1, 900.
Eureka Math Precalculus Module 3 Lesson 21 Exit Ticket Answer Key
Question 1.
Darrin drank a latte with 205 milligrams (mg) of caffeine. Each hour, the caffeine in Darrin’s body diminishes by about 8%.
a. Write a formula to model the amount of caffeine remaining in Darrin’s system after each hour.
Answer:
c(t) = 205 ⋅ (1 – 8%)t
c(t) = 205 ⋅ (0.92)t
b. Write a formula to model the number of hours since Darrin drank his latte based on the amount of caffeine in Darrin’s system.
Answer:
c = 205(0.92)t
\(\frac{c}{205}\) = 0.92t
\(\ln \left(\frac{c}{205}\right)\) = ln(0.92)t
\(\ln \left(\frac{c}{205}\right)\) = t∙ln(0.92)
t = \(\frac{\ln \left(\frac{c}{205}\right)}{\ln (0.92)}\)
Thus,
t(c) = \(\frac{\ln \left(\frac{c}{205}\right)}{\ln (0.92)}\).
Alternatively,
c = 205(0.92)t
\(\frac{c}{205}\) = 0.92t
\(\log _{0.92}\left(\frac{c}{205}\right)\) = t.
And by the change of base property,
t(c) = \(\frac{\ln \left(\frac{c}{205}\right)}{\ln (0.92)}\).
c. Use your equation in part (b) to find how long it takes for the caffeine in Darrin’s system to drop below 50 mg.
Answer:
t = \(\frac{\ln \left(\frac{50}{205}\right)}{\ln (0.92)}\)
It would take approximately 16.922 hours for the caffeine to drop to 50 mg; therefore, it would take approximately 17 hours for the caffeine to drop below 50 mg.