Engage NY Eureka Math Precalculus Module 3 Lesson 18 Answer Key
Eureka Math Precalculus Module 3 Lesson 18 Example Answer Key
Exercises
Suppose ABC Electric purchases a new work truck for $34, 500. They estimate that the truck’s value will depreciate to $0 over 15 years. The table below shows the value v(t) of the truck in thousands of dollars depreciated over time t in months using a straight-line depreciation method.

Exercise 1.
Does the function v appear to be a linear function? Explain your reasoning.
Answer:
Yes. Each time the months increase by 12, the value decreases by 2.3.
Exercise 2.
What is an appropriate domain and range for v in this situation?
Answer:
The domain would be [0, 180], which represents a time span of 15 years measured in months. The range would be [0, 34.5], which represents the value of the car over the 15-year period based on the company’s estimates.
Exercise 3.
Write a formula for v in terms of t, the months since the truck was purchased.
Answer:
v(t) = –\(\frac{2.3}{12}\) t + 34.5 for 0≤t≤180
Exercise 4.
What will the truck be worth after 30 months? 40 months? 50 months?
Answer:
All values are rounded to the hundredths place.
v(30) = 28.75
v(40) = 26.83
v(50) = 24.92
Exercise 5.
When will the truck be valued at $30, 000? $20, 000? $10, 000?
Answer:
v(t) = 30 when
–\(\frac{2.3}{12}\) x + 34.5 = 30
To solve for t, subtract both sides of the equation by 34.5, and then multiply both sides by –\(\frac{12}{2.3}\).
–\(\frac{2.3}{12}\) t + 34.5-34.5 = 30-34.5
–\(\frac{2.3}{12}\) t = -4.5
–\(\frac{12}{2.3}\) (-\(\frac{2.3}{12}\)t) = –\(\frac{12}{2.3}\) (-4.5)
t≈23.48
After approximately 23.5 months, the truck will be worth $30, 000.
Similarly, solving the equations v(t) = 20000 and v(t) = 10000 will give approximate times for when the truck is worth $20, 000 and $10, 000. The truck will be worth $20, 000 after approximately 75.7 months, and it will be worth $10, 000 after approximately 127.8 months.
Exercise 6.
Construct a table that shows the time of depreciation, t(v), in months as a function of the value of the truck, v, in thousands of dollars.
Answer:

Exercise 7.
Does the function t appear to be a linear function? Explain your reasoning.
Answer:
Yes. Each time the v values decrease by 2.3, the t(v) values increase by 12.
Exercise 8.
What is an appropriate domain and range for t in this situation?
Answer:
The domain and range are the same as for the function v, except switched.
Exercise 9.
Write a formula for t in terms of the value of the truck, v, since it was purchased.
Answer:
Using the slope of the t function, –\(\frac{12}{2.3}\), and a point (34.5, 0), we could create the equation t(v) = –\(\frac{12}{2.3}\) (v-34.5) + 0.
Exercise 10.
Explain how you can create the formula for t using the formula for v from Exercise 5.
Answer:
Solve v(t) = y for t, and then just change the variables.
–\(\frac{2.3}{12}\) t + 34.5 = y
–\(\frac{2.3}{12}\) t = y – 34.5
t = –\(\frac{12}{2.3}\)(y-34.5)
Thus, t(v) = –\(\frac{12}{2.3}\) (v-34.5) for 0 ≤ v ≤ 34.5.
Exercise 11.
Sketch a graph of the equations y = v(t) and y = t(v) in the Cartesian plane. How do their graphs compare?
Answer:
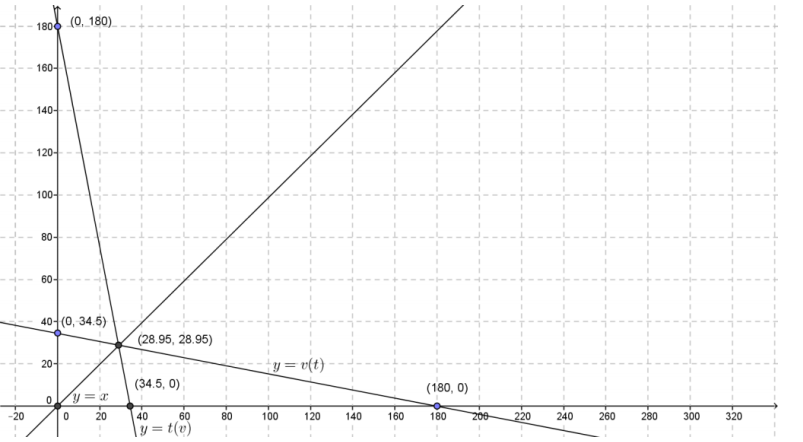
Both graphs are decreasing, and they intersect at the point (28.95, 28.95).
Exercise 12.
What is the meaning of the intersection point of the graphs of the two equations?
Answer:
It is the point where the value of the truck (in thousands of dollars) is equal to the number of months that its value has depreciated since its purchase.
Exercise 13.
Add the graph of y = x to your work in Exercise 11. Describe the relationship between the graphs of y = v(t), y = t(v), and y = x.
Answer:
The graphs of y = v(t) and y = t(v) are images of one another across the line y = x.
Exercise 14.
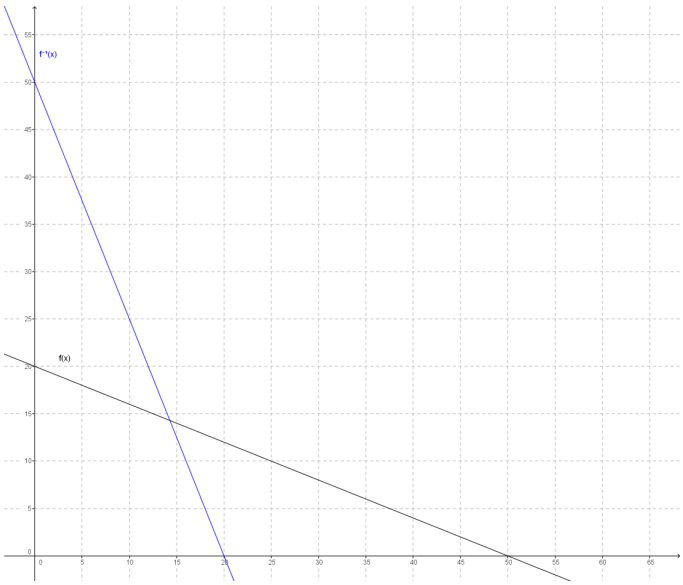
ABC Electric uses this formula, f(x) = 750-10x, to depreciate computers, where f is the value of a computer and x is the number of months since its purchase.
a. Calculatef(36). What is the meaning of f(36)?
Answer:
f(36) = 750 – 10(36) = 390
It is the value of a computer 36 months after the date it is purchased.
b. What is the meaning of b in f(b) = 60? What is the value of b?
Answer:
It is the number of months since its purchase date when the computer will be worth $60. Solving 750 – 10b = 60 gives a value of b = 69.
c. Write a formula for f-1, and explain what it means in this situation.
Answer:
f-1 (x) = \(\frac{x-750}{-10}\)
This function determines the number of months that have passed since the computer’s date of purchase given the value of the computer, x dollars.
d. When will the depreciated value of a computer be less than $400?
Answer:
Evaluate f-1 (400).
f-1 (x) = \(\frac{400-750}{-10}\) = \(\frac{-350}{-10}\) = 35
The value of a computer will be less than $400 after 35 months.
e. What is the meaning of c in f-1 (c) = 60? What is the value of c?
Answer:
It is the value of the computer 60 months after its date of purchase.
To find the value of c, you can evaluate f(60), or you can solve the equation \(\frac{c-750}{-10}\) = 60 for c.
The value of c is 150. After 60 months, the value of the computer is $150.
Exercise 15.
Find the inverses of the following functions:
a. f(x) = \(\frac{2}{3}\) x – 10
Answer:
y = \(\frac{2}{3}\) x – 10
x = \(\frac{2}{3}\) y – 10
x + 10 = \(\frac{2}{3}\) y
y = \(\frac{3}{2}\) (x + 10)
f-1 (x) = \(\frac{3}{2}\)(x + 10)
b. g(x) = 2(x + 4)3
Answer:
y = 2(x + 4)3
x = 2(y + 4)3
\(\frac{x}{2}\) = (y + 4)3
\(\sqrt[3]{\frac{x}{2}}\) = y + 4
y = \(\sqrt[3]{\frac{x}{2}}-4\)
g-1 (x) = \(\sqrt[3]{\frac{x}{2}}-4\)
c. h(x) = \(\frac{1}{x-2}\), x ≠ 2
Answer:
y = \(\frac{1}{x-2}\)
x = \(\frac{1}{y-2}\)
x(y – 2) = 1
xy – 2x = 1
xy = 1 + 2x
y = \(\frac{1 + 2x}{x}\), x ≠ 0
h-1 (x) = \(\frac{1 + 2x}{x}\), x ≠ 0
Eureka Math Precalculus Module 3 Lesson 18 Problem Set Answer Key
Question 1.
For each of the following, write the inverse of the function given.
a. f = {(1, 3), (2, 15), (3, 8), (4, -2), (5, 0)}
Answer:
f-1 = {(3, 1), (15, 2), (8, 3), (-2, 4), (0, 5)}
b. g = {(0, 5), (2, 10), (4, 15), (6, 20)}
Answer:
g-1 = {(5, 0), (10, 2), (15, 4), (20, 6)}
c. h = {(1, 5), (2, 25), (3, 125), (4, 625)}
Answer:
h-1 = {(5, 1), (25, 2), (125, 3), (625, 4)}
d. 
Answer:

e. 
Answer:

f. 
Answer:

g. y = 2x
Answer:
y = \(\frac{1}{2}\) x
h. y = \(\frac{1}{3}\) x
Answer:
y = 3x
i. y = x – 3
Answer:
y = x + 3
j. y = –\(\frac{2}{3}\) x + 5
Answer:
y = –\(\frac{3}{2}\) x + \(\frac{15}{2}\)
k. 2x – 5y = 1
Answer:
2y-5x = 1
l. -3x + 7y = 14
Answer:
-3y + 7x = 14
m. y = \(\frac{1}{3}\) (x-9)3
Answer:
y = \(\sqrt[3]{3 x}\) + 9
n. y = \(\frac{5}{3x-4}\), x ≠ \(\frac{4}{3}\)
Answer:
y = \(\frac{5}{3x}\) + \(\frac{4}{3}\)
o. y = 2x7 + 1
Answer:
y = \(\sqrt[7]{\frac{1}{2} x-\frac{1}{2}}\)
p. y = \(\sqrt[5]{x}\)
Answer:
y = x5
q. y = \(\frac{x + 1}{x-2}\), x ≠ 1
Answer:
y = \(\frac{x + 1}{x-1}\)
Question 2.
For each part in Problem 1, state the domain, D, and range, R, of the inverse function.
Answer:
a. D = {-2, 0, 3, 8, 15}
R = {0, 1, 2, 3, 4, 5}
b. D = {5, 10, 15, 20}
R = {0, 2, 4, 6}
c. D = {5, 25, 125, 625}
R = {1, 2, 3, 4}
d. D = {3, 12, 27, 48}
R = {1, 2, 3, 4}
e. D = {3, 6, 12, 24}
R = {-1, 0, 1, 2}
f. D = {0, 1, 2, 3}
R = {1, 10, 100, 1000}
g. Both domain and range are all real numbers.
h. Both domain and range are all real numbers.
i. Both domain and range are all real numbers.
j. Both domain and range are all real numbers.
k. Both domain and range are all real numbers.
l. Both domain and range are all real numbers.
m. Both domain and range are all real numbers.
n. The domain is all real numbers except x = 0, and the range is all real numbers except y = \(\frac{4}{3}\).
o. Both domain and range are all real numbers.
p. Both domain and range are all real numbers.
q. Both domain and range are all real numbers except 1.
Question 3.
Sketch the graph of the inverse function for each of the following functions:
a.
Answer:
b.
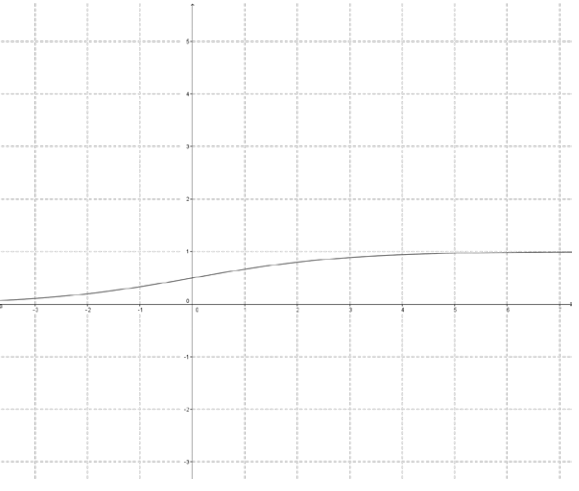
Answer:
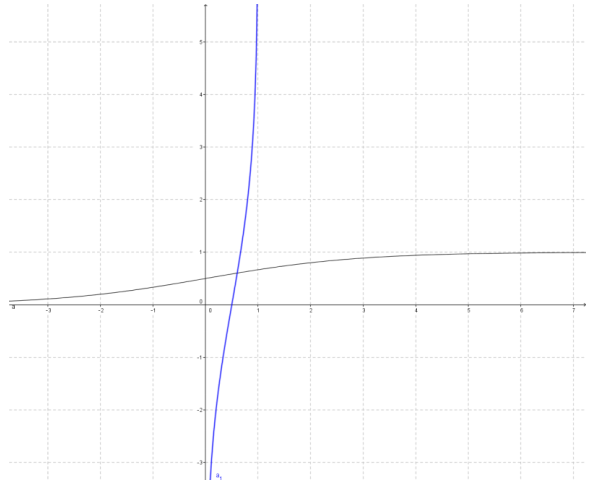
c.
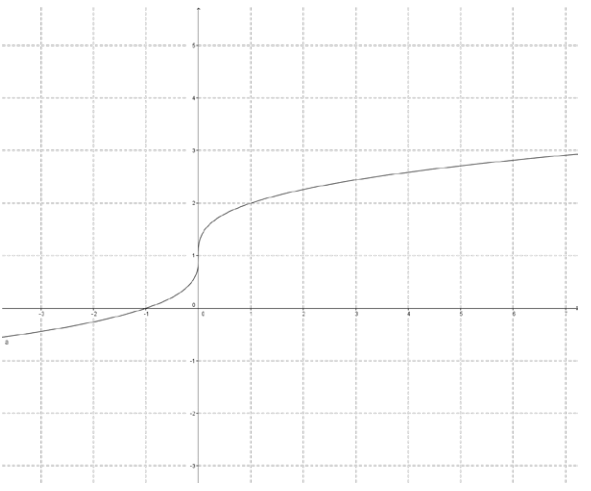
Answer:
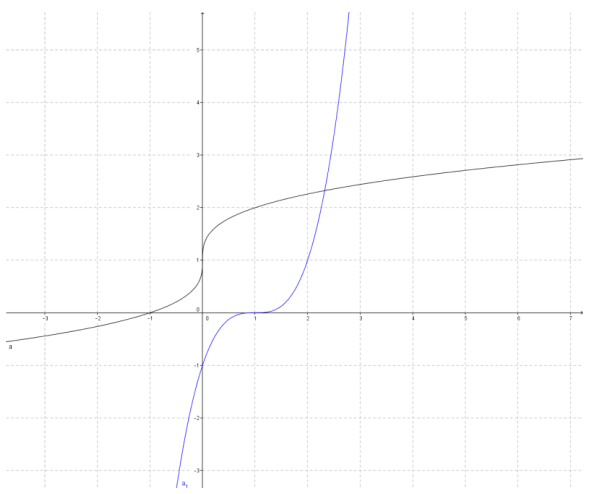
d.
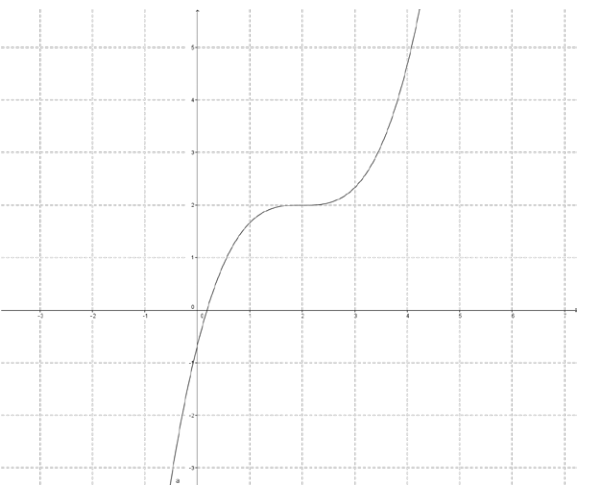
Answer:
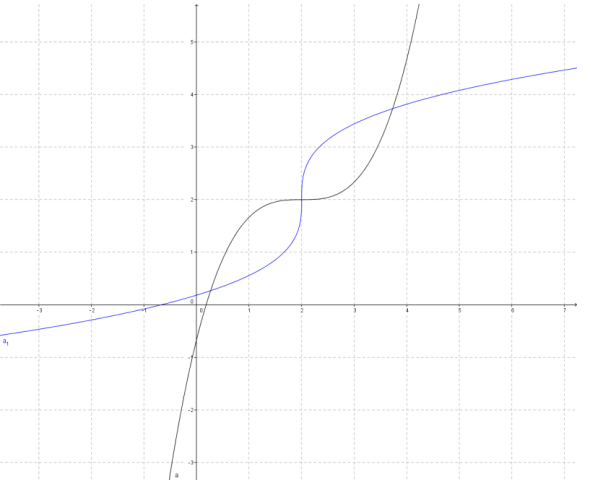
Question 4.
Natalie thinks that the inverse of f(x) = x – 5 is g(x) = 5 – x. To justify her answer, she calculates f(5) = 0 and then finds g(0) = 5, which gives back the original input.
a. What is wrong with Natalie’s reasoning?
Answer:
A single point does not verify that the function is an inverse function. In order to be an inverse of the original function, we must have f(g(x)) = g(f(x)) for all x.
b. Show that Natalie is incorrect by using other examples from the domain and range of f.
Answer:
Any other point will work; for instance, f(0) = -5 and g(-5) = 10.
c. Find -1 (x). Where do -1 and g intersect?
Answer:
-1 (x) = x + 5
The two functions intersect at the point (0, 5), which explains why Natalie thought g was the inverse of f after she tried that point.
Question 5.
Sketch a graph of the inverse of each function graphed below by reflecting the graph about the line y = x. State whether or not the inverse is a function.
a.
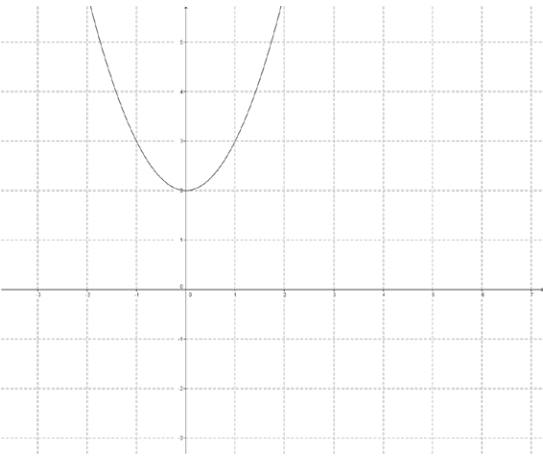
Answer:
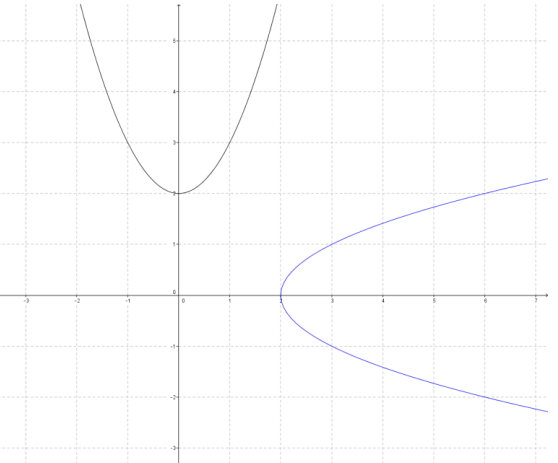
The reflected image is not a function.
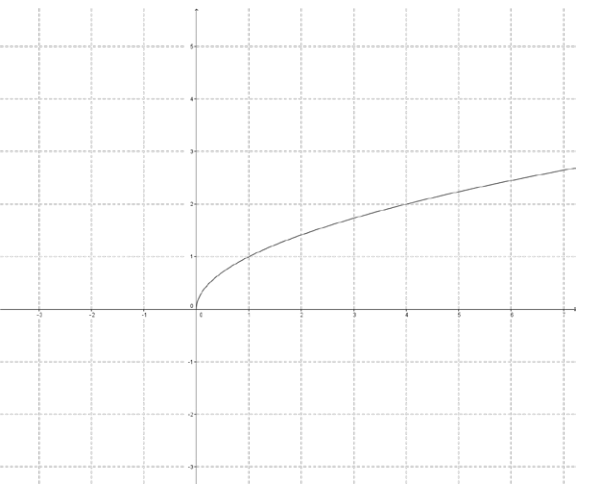
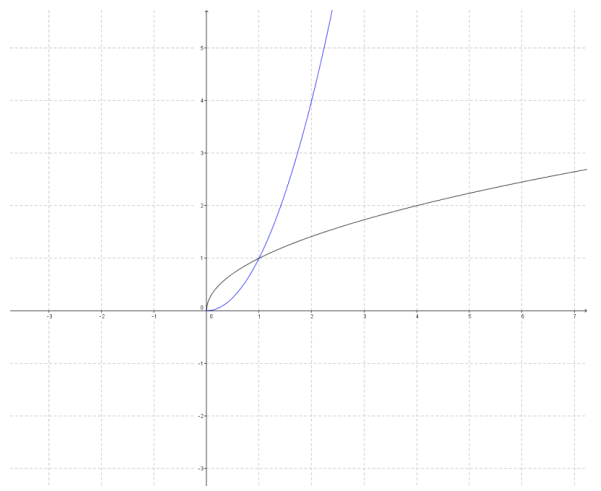
b.
Answer:
The reflected image is not a function.
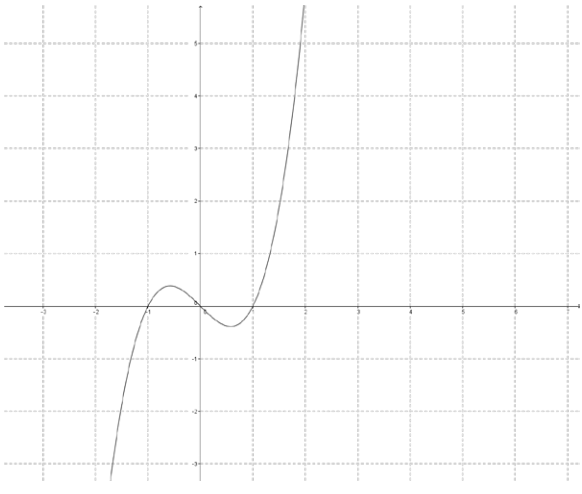
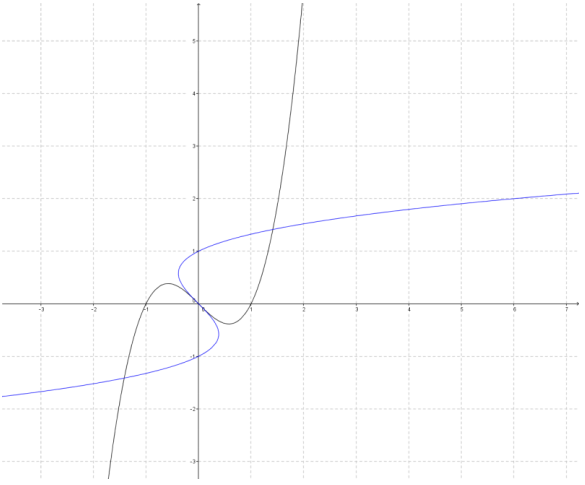
c.
Answer:
The reflected image is a function.
d.
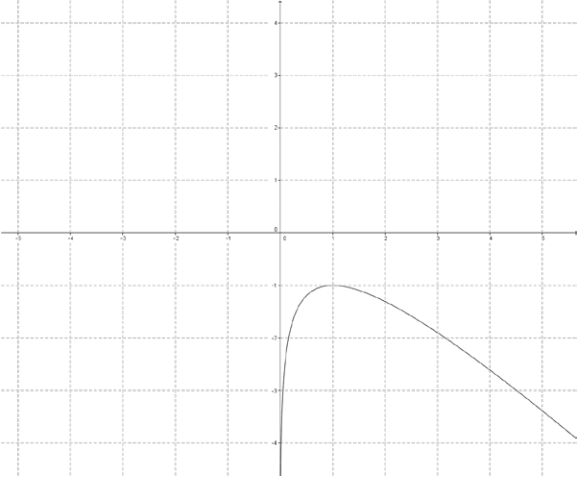
Answer:
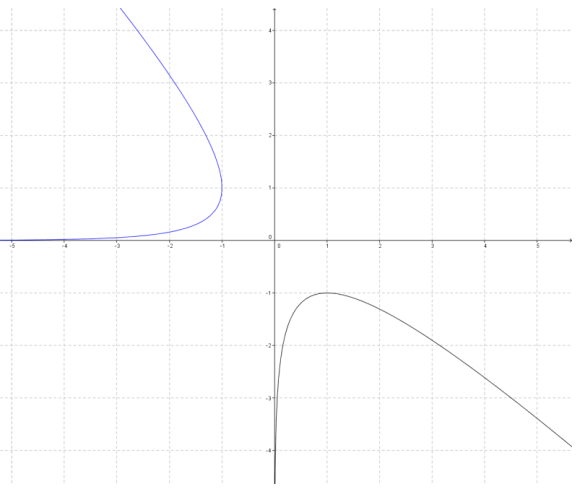
The reflected image is not a function.
Question 6.
How can you tell before you reflect a graph over y = x if its reflection will be a function or not?
Answer:
If the function is not one-to-one, then its reflection will not be a function. Algebraically, if f(x1) = f(x2) and x1 ≠ x2, then the reflection will not be a function. Visually, this takes on the shape of a horizontal line intersecting the graph at two points. If any horizontal line can intersect the graph of a function at two points, then the reflection of the graph over the line y = x will not be a function.
Question 7.
After finding several inverses, Callahan exclaims that every invertible linear function intersects its inverse at some point. What needs to be true about the linear functions that Callahan is working with for this to be true? What is true about linear functions that do not intersect their inverses?
Answer:
The linear functions Callahan is working with must have slopes different from 1 in order to intersect with their inverses since this will guarantee that the functions will cross the y = x line and that the inverses will intersect at y = x, if they intersect at all. If a linear function is parallel to y = x, then it will not intersect the graph of its inverse function.
Question 8.
If f is an invertible function such that f(x) > x for all x, then what do we know about the inverse of f?
Answer:
Since the function is always above the line y = x, we know that its inverse will always be below the line y = x. In other words, f-1(x) < x. We can also see this by substituting y = f(x), which gives us y > x. Switching x and y to find the inverse, we get x > y or x > f-1(x).
Question 9.
Gavin purchases a new $2, 995 computer for his business, and when he does his taxes for the year, he is given the following information for deductions on his computer (this method is called MACRS—Modified Accelerated Cost Recovery System):

Where P0 represents the value of the computer new.
a. Construct a table for the function D, giving the deduction Gavin can claim in year x for his computer, x = {1, 2, 3}.
Answer:

b. Find the inverse of D.
Answer:

c. Construct a table for the function P, giving the present value of Gavin’s computer in year x, x = {0, 1, 2, 3}.
Answer:

d. Find the inverse of P.
Answer:

Question 10.
Problem 9 used the MACRS method to determine the possible deductions Gavin could have for the computer he purchased. The straight-line method can be used also. Assume the computer has a salvage value of $500 after 5 years of use; call this value S. Then, Gavin would be presented with this information when he does his taxes:

a. Construct a table for the function D, giving the deduction Gavin can claim in year x for his computer in x = {1, 2, 3, 4, 5}.
Answer:

b. What do you notice about the function for deduction in this problem compared to the function in Problem 9?
Answer:
The deduction values are a lot lower, and after the first year they are constant.
c. If you are given the deduction that Gavin claims in a particular year using the straight-line method, is it possible for you to know what year he claimed it in? Explain. What does this tell us about the inverse of D?
Answer:
Unless it is the first year, you cannot tell the year in which Gavin claimed a particular deduction just by knowing the deduction amount. Gavin should claim $499 as a deduction every year except for the first year.
Extension:
Question 11.
For each function in Problem 1, verify that the functions are inverses by composing the function with the inverse you found (in each case, after applying both functions, you should end up with the original input).
Answer:
a. f-1 (f(1)) = f-1 (3) = 1
f-1 (f(2)) = f-1 (15) = 2
f-1 (f(3)) = f-1 (8) = 3
f-1 (f(4)) = f-1 (-2) = 4
f-1 (f(5)) = f-1 (0) = 5
b. f f-1
0 → 5 → 0
2 → 10 → 2
4 → 15 → 4
6 → 20 → 6
c. h(h-1 (5)) = h(1) = 5
h(h-1 (25)) = h(2) = 25
h(h-1 (125)) = h(3) = 125
h(h-1 (625)) = h(4) = 625
d. f-1 f
3 → 1 → 3
12 → 2 → 12
27 → 3 → 27
48 → 4 → 48
e. 
f. 
g. Let y = f(x).
f-1 (f(x)) = \(\frac{1}{2}\) (2x)
= x
h. Let y = f(x).
f-1 (f(x)) = 3(\(\frac{1}{3}\) x)
= x
i. Let y = f(x).
f-1 (f(x)) = (x – 3) + 3
= x
j. Let y = f(x).
f-1 (f(x)) = –\(\frac{3}{2}\) (-\(\frac{2}{3}\) x + 5) + \(\frac{15}{2}\)
= x-\(\frac{15}{2}\) + \(\frac{15}{2}\)
= x
k. Let y = f(x); then f(x) = \(\frac{2}{5}\) x-\(\frac{1}{5}\), f-1 (x) = \(\frac{5}{2}\) x + \(\frac{1}{2}\).
f-1 (f(x)) = \(\frac{5}{2}\) (\(\frac{2}{5}\) x-\(\frac{1}{5}\)) + \(\frac{1}{2}\)
= x – \(\frac{1}{2}\) + \(\frac{1}{2}\)
= x
l. Let y = f(x); then f(x) = \(\frac{3}{7}\) x + 2 and f-1 (x) = \(\frac{7}{3}\) x-\(\frac{14}{3}\).
f-1 (f(x)) = \(\frac{7}{3}\) (\(\frac{3}{7}\) x + 2)-\(\frac{14}{3}\)
= x + \(\frac{14}{3}\)–\(\frac{14}{3}\)
= x
m. Let y = f(x).
f-1 (f(x)) = \(\sqrt[3]{3\left(\frac{1}{3}(x-9)^{3} + 9 \mid\right.}\)
= \(\sqrt[3]{(1)(x-9)^{3}} + 9\)
= x – 9 + 9
= x
n. Let y = f(x).
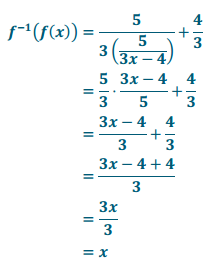
o. Let y = f(x).
f-1 (f(x)) = \(\sqrt[7]{\frac{1}{2}\left(2 x^{7} + 1\right)-\frac{1}{2}}\)
= \(\sqrt[7]{x^{7} + \frac{1}{2}-\frac{1}{2}}\)
= \(\sqrt[7]{x^{7}}\)
= x
p. Let y = f(x).
f-1 (f(x)) = \((\sqrt[5]{x})^{5}\)
= x
q. Let y = f(x).
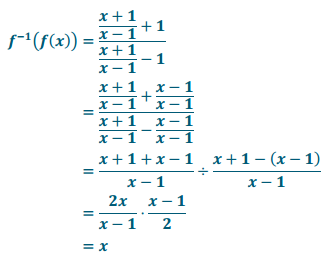
Eureka Math Precalculus Module 3 Lesson 18 Exit Ticket Answer Key
Question 1.
The function f is described below in three different ways. For each way, express f-1 in the same style.

f(x) = –\(\frac{2}{5}\) x + 20
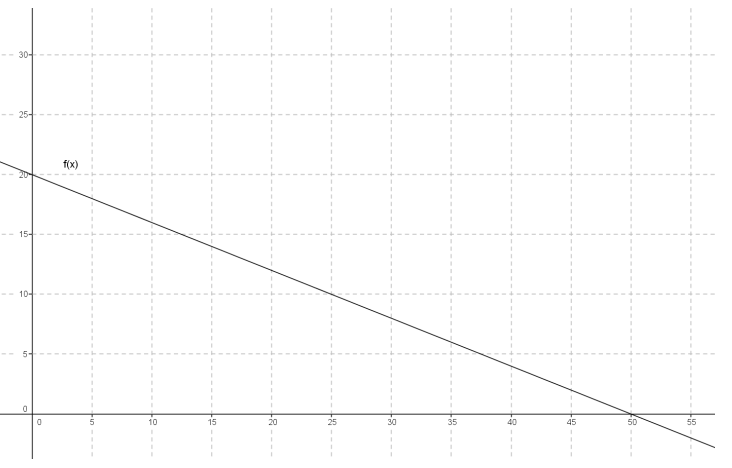
Answer:

f(x) = –\(\frac{2}{5}\) x + 20
f-1 (x) = –\(\frac{5}{2}\) x + 50