Engage NY Eureka Math Precalculus Module 3 Lesson 10 Answer Key
Eureka Math Precalculus Module 3 Lesson 10 Exercise Answer Key
Opening Exercise
a. Add the fractions: \(\frac{3}{5}\) + \(\frac{2}{7}\).
Answer:
\(\frac{3}{5}\) + \(\frac{2}{7}\) = \(\frac{3}{5}\) ∙ \(\frac{7}{7}\) + \(\frac{2}{7}\) ∙ \(\frac{5}{5}\) = \(\frac{21}{35}\) + \(\frac{10}{35}\) = \(\frac{31}{35}\)
b. Subtract the fractions: \(\frac{5}{2}\) – \(\frac{4}{3}\).
Answer:
\(\frac{5}{2}\) – \(\frac{4}{3}\) = \(\frac{5}{2}\) ∙ \(\frac{3}{3}\) – \(\frac{4}{3}\) ∙ \(\frac{2}{2}\) = \(\frac{15}{6}\) – \(\frac{8}{6}\) = \(\frac{7}{6}\)
c. Add the expressions: \(\frac{3}{x}\) + \(\frac{x}{5}\).
Answer:
\(\frac{3}{x}\) + \(\frac{x}{5}\) = \(\frac{3}{x}\) ∙ \(\frac{5}{5}\) + \(\frac{x}{5}\) ∙ \(\frac{x}{x}\) = \(\frac{15}{5 x}\) + \(\frac{x^{2}}{5 x}\) = \(\frac{15 + x^{2}}{5 x}\)
d. Subtract the expressions: \(\frac{x}{x + 2}\) – \(\frac{3}{x + 1}\).
Answer:
\(\frac{x}{x + 2}\) – \(\frac{3}{x + 1}\) = \(\frac{x}{x + 2}\) ∙ \(\frac{x + 1}{x + 1}\) – \(\frac{3}{x + 1}\) ∙ \(\frac{x + 2}{x + 2}\) = \(\frac{x^{2} + x}{(x + 2)(x + 1)}\) – \(\frac{3 x + 6}{(x + 1)(x + 2)}\) = \(\frac{\left(x^{2} + x\right) – (3 x + 6)}{(x + 2)(x + 1)}\) = \(\frac{x^{2} – 2 x – 6}{(x + 2)(x + 1)}\)
Exercises
Exercise 1.
Construct an argument that shows that the set of rational numbers is closed under addition. That is, if x and y are rational numbers and w = x + y, prove that w must also be a rational number.
Answer:
Since x and y are rational numbers, there are four integers, a, b, c, and d, with x = \(\frac{a}{b}\) and y = \(\frac{c}{d}\), and neither b nor d is 0.
Now we need to check to see if w is a rational number:
w = x + y = \(\frac{a}{b}\) + \(\frac{c}{d}\) = \(\frac{a}{b}\) ∙ \(\frac{d}{d}\) + \(\frac{c}{d}\) ∙ \(\frac{b}{b}\) = \(\frac{ad + cb}{bd}\)
The numerator is formed by multiplying and adding integers, so it must be an integer. Similarly, the denominator must be an integer. Lastly, bd cannot be 0 since neither b nor d is 0. This proves that w is a rational number.
Exercise 2.
How could you modify your argument to show that the set of rational numbers is also closed under subtraction? Discuss your response with another student.
Answer:
This time, we start with \(\frac{a}{b}\) – \(\frac{c}{d}\) and end up with \(\frac{ad – cb}{bd}\). We just notice that subtracting two integers yields an integer and then apply the same reasoning as before.
Exercise 3.
Multiply the fractions: \(\frac{2}{5}\) ∙ \(\frac{3}{4}\).
Answer:
\(\frac{2}{5}\) ∙ \(\frac{3}{4}\) = \(\frac{6}{20}\)
Exercise 4.
Divide the fractions: \(\frac{2}{5}\) ÷ \(\frac{3}{4}\).
Answer:
\(\frac{2}{5}\) ÷ \(\frac{3}{4}\) = \(\frac{2}{5}\) ∙ \(\frac{4}{3}\) = \(\frac{8}{15}\)
Exercise 5.
Multiply the expressions: \(\frac{x + 1}{x + 2}\) ∙ \(\frac{3x}{x – 4}\).
Answer:
\(\frac{x + 1}{x + 2}\) ∙ \(\frac{3x}{x – 4}\) = \(\frac{(x + 1) \cdot 3 x}{(x + 2)(x – 4)}\)
Exercise 6.
Divide the expressions: \(\frac{x + 1}{x + 2}\) ÷ \(\frac{3x}{x – 4}\).
Answer:
\(\frac{x + 1}{x + 2}\) ÷ \(\frac{3x}{x – 4}\) = \(\frac{x + 1}{x + 2}\) ∙ \(\frac{x – 4}{3x}\) = \(\frac{(x + 1)(x – 4)}{(x + 2) \cdot 3 x}\)
Exercise 7.
Construct an argument that shows that the set of rational numbers is closed under division. That is, if x and y are rational numbers (with y nonzero) and w = \(\frac{x}{y}\), prove that w must also be a rational number.
Answer:
Let x = \(\frac{a}{b}\) and let y = \(\frac{c}{d}\), with both b and d nonzero.
\(\frac{a}{b}\) ÷ \(\frac{c}{d}\) = \(\frac{a}{b}\) ∙ \(\frac{d}{c}\) = \(\frac{ad}{bc}\)
This is indeed a rational number. Thus, the set of rational numbers is closed under division by a nonzero number.
Exercise 8.
How could you modify your argument to show that the set of rational expressions is also closed under division by a nonzero rational expression? Discuss your response with another student.
Answer:
The only change is that a, b, c, and d represent polynomials rather than integers. The numerator and denominator of the quotient are polynomials because they both represent the product of polynomials, and polynomials are closed under multiplication. This means that the quotient is a ratio of polynomials, which fits our definition of a rational expression.
Eureka Math Precalculus Module 3 Lesson 10 Problem Set Answer Key
Question 1.
Given \(\frac{x + 1}{x – 2}\) and \(\frac{x – 1}{x^{2} – 4}\), show that performing the following operations results in another rational expression.
a. Addition
Answer:
\(\frac{x + 1}{x – 2}\) + \(\frac{x – 1}{x^{2} – 4}\) = \(\frac{x^{2} + 3 x + 2 + x – 1}{x^{2} – 4}\) = \(\frac{x^{2} + 4 x + 1}{x^{2} – 4}\)
b. Subtraction
Answer:
\(\frac{x + 1}{x – 2}\) – \(\frac{x – 1}{x^{2} – 4}\) = \(\frac{x^{2} + 3 x + 2 – x + 1}{x^{2} – 4}\) = \(\frac{x^{2} + 2 x + 3}{x^{2} – 4}\)
c. Multiplication
Answer:
\(\frac{x + 1}{x – 2}\) ∙ \(\frac{x – 1}{x^{2} – 4}\) = \(\frac{x^{2} – 1}{(x – 2)\left(x^{2} – 4\right)}\)
d. Division
Answer:
\(\frac{x + 1}{x – 2}\) ÷ \(\frac{x – 1}{x^{2} – 4}\) = \(\frac{x^{2} + 3 x + 2}{x – 1}\)
Question 2.
Find two rational expressions \(\frac{a}{b}\) and \(\frac{c}{d}\) that produce the result \(\frac{x – 1}{x^{2}}\) when using the following operations. Answers for each type of operation may vary. Justify your answers.
a. Addition
Answer:
\(\frac{x}{x^{2}}\) + \(\frac{ – 1}{x^{2}}\) = \(\frac{x – 1}{x^{2}}\)
b. Subtraction
Answer:
\(\frac{x}{x^{2}}\) – \(\frac{1}{x^{2}}\) = \(\frac{x – 1}{x^{2}}\)
c. Multiplication
Answer:
\(\frac{1}{x}\) ∙ \(\frac{x – 1}{x}\) = \(\frac{x – 1}{x^{2}}\)
d. Division
Answer:
\(\frac{1}{x}\) ÷ \(\frac{x}{x – 1}\) = \(\frac{x – 1}{x^{2}}\)
Question 3.
Find two rational expressions \(\frac{a}{b}\) and \(\frac{c}{d}\) that produce the result \(\frac{2 x + 2}{x^{2} – x}\) when using the following operations. Answers for each type of operation may vary. Justify your answers.
a. Addition
Answer:
\(\frac{2 x}{x^{2} – x}\) + \(\frac{2}{x^{2} – x}\) = \(\frac{2 x + 2}{x^{2} – x}\)
b. Subtraction
Answer:
\(\frac{2 x}{x^{2} – x}\) – \(\frac{ – 2}{x^{2} – x}\) = \(\frac{2 x + 2}{x^{2} – x}\)
c. Multiplication
Answer:
\(\frac{2}{x}\) ∙ \(\frac{x + 1}{x – 1}\) = \(\frac{2 x + 2}{x^{2} – x}\)
d. Division
Answer:
\(\frac{2}{x}\) ÷ \(\frac{x – 1}{x + 1}\) = \(\frac{2 x + 2}{x^{2} – x}\)
Question 4.
Consider the rational expressions A, B and their quotient, \(\frac{A}{B}\), where B is not equal to zero.
a. For some rational expression C, does \(\frac{AC}{BC}\) = \(\frac{A}{B}\)?
Answer:
Whenever C≠0, \(\frac{AC}{BC}\) = \(\frac{A}{B}\).
b. Let A = \(\frac{x}{y}\) + \(\frac{1}{x}\) and B = \(\frac{y}{x}\) + \(\frac{1}{y}\). What is the least common denominator of every term of each expression?
Answer:
xy
c. Find AC, BC where C is equal to your result in part (b). Then, find \(\frac{AC}{BC}\). Simplify your answer.
Answer:
AC = x2 + y
BC = y2 + x
\(\frac{AC}{BC}\) = \(\frac{x^{2} + y}{y^{2} + x}\)
d. Express each rational expression A, B as a single rational term, that is, as a division between two polynomials.
Answer:
A = \(\frac{x^{2} + y}{x y}\)
B = \(\frac{y^{2} + x}{x y}\)
e. Write \(\frac{A}{B}\) as a multiplication problem.
Answer:
\(\frac{A}{B}\) = A ∙ \(\frac{1}{B}\)
f. Use your answers to parts (d) and (e) to simplify \(\frac{A}{B}\).
Answer:
\(\frac{A}{B}\) = \(\frac{x^{2}+y}{x y}\) ∙ \(\frac{x y}{y^{2}+x}\)
= \(\frac{x^{2}+y}{y^{2}+x}\)
g. Summarize your findings. Which method do you prefer using to simplify rational expressions?
Answer:
We can simplify complex rational expressions by either multiplying both the numerators and denominators by the least common denominator, or we can use the fact that division by a number is multiplication by its reciprocal. Answers may vary on preference.
Question 5.
Simplify the following rational expressions.
a. \(\frac{\frac{1}{y} – \frac{1}{x}}{\frac{x}{y} – \frac{y}{x}}\)
Answer:
\(\frac{\frac{1}{y} – \frac{1}{x}}{\frac{x}{y} – \frac{y}{x}}\) = \(\frac{\frac{x – y}{x y}}{\frac{x^{2} – y^{2}}{x y}}\) = \(\frac{1}{x + y}\)
b. \(\frac{\frac{1}{x} + \frac{1}{y}}{\frac{1}{x^{2}} – \frac{1}{y^{2}}}\)
Answer:
\(\frac{\frac{1}{x} + \frac{1}{y}}{\frac{1}{x^{2}} – \frac{1}{y^{2}}}\) = \(\frac{1}{\frac{1}{x} – \frac{1}{y}}\) = \(\frac{x y}{y – x}\)
c. \(\frac{\frac{1}{x^{4}} – \frac{1}{y^{2}}}{\frac{1}{x^{4}} + \frac{2}{x^{2} y} + \frac{1}{y^{2}}}\)
Answer:
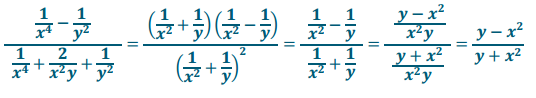
d. \(\frac{\frac{1}{x – 1} – \frac{1}{x}}{\frac{1}{x – 1} + \frac{1}{x}}\)
Answer:
\(\frac{\frac{x – x + 1}{(x – 1) x}}{\frac{x + x – 1}{(x – 1) x}}\) = \(\frac{1}{2 x – 1}\)
Question 6.
Find A and B that make the equation true. Verify your results.
a. \(\frac{A}{x + 1}\) + \(\frac{B}{x – 1}\) = \(\frac{2}{x^{2} – 1}\)
Answer:
\(\frac{A(x – 1) + B(x + 1)}{(x + 1)(x – 1)}\) = \(\frac{2}{(x + 1)(x – 1)}\)
Therefore,
A(x – 1) + B(x + 1) = 2.
Let x = 1, A = – 1
Let x = – 1, B = 1
– \(\frac{1}{x + 1}\) + \(\frac{1}{x – 1}\) = \(\frac{2}{x^{2} – 1}\)
b. \(\frac{A}{x + 3}\) + \(\frac{B}{x + 2}\) = \(\frac{2 x – 1}{x^{2} + 5 x + 6}\)
Answer:
\(\frac{A(x + 2) + B(x + 3)}{(x + 3)(x + 2)}\) = \(\frac{2 x – 1}{(x + 3)(x + 2)}\)
Therefore,
A(x + 2) + B(x + 3) = 2x – 1.
Let x = – 3, A = 7
Let x = – 2, B = – 5
\(\frac{7}{x + 3}\) – \(\frac{5}{x + 2}\) = \(\frac{2 x – 1}{x^{2} + 5 x + 6}\)
Question 7.
Find A, B, and C that make the equation true. Verify your result.
\(\frac{A x + B}{x^{2} + 1}\) + \(\frac{C}{x + 2}\) = \(\frac{x – 1}{\left(x^{2} + 1\right)(x + 2)}\)
Answer:
\(\frac{A x + B}{x^{2} + 1}\) + \(\frac{C}{x + 2}\) = \(\frac{x – 1}{\left(x^{2} + 1\right)(x + 2)}\), (Ax + B)(x + 2) + C(x2 + 1) = x – 1,
Ax2 + 2Ax + Bx + 2B + Cx2 + C = x – 1
Therefore,
A + C = 0, 2A + B = 1
and 2B + C = – 1.
A = \(\frac{3}{5}\), B = – \(\frac{1}{5}\), C = – \(\frac{3}{5}\)
\(\frac{\frac{3}{5} x – \frac{1}{5}}{x^{2} + 1}\) + \(\frac{ – \frac{3}{5}}{x + 2}\) = \(\frac{x – 1}{\left(x^{2} + 1\right)(x + 2)}\)
Eureka Math Precalculus Module 3 Lesson 10 Exit Ticket Answer Key
Question 1.
Payton says that rational expressions are not closed under addition, subtraction, multiplication, or division. His claim is shown below. Is he correct for each case? Justify your answers.
a. \(\frac{x}{2x + 1}\) + \(\frac{x + 1}{2x + 1}\) = 1, and 1 is a whole number, not a rational expression.
Answer:
No, he is not correct. \(\frac{x}{2x + 1}\) + \(\frac{x + 1}{2x + 1}\) = \(\frac{2x + 1}{2x + 1}\) The numerator and denominator are both polynomials.
b. \(\frac{3x – 1}{2x + 1}\) – \(\frac{3x – 1}{2x + 1}\) = 0, and 0 is a whole number, not a rational expression.
Answer:
No, he is not correct. 0 = \(\frac{0}{1}\) The numerator and denominator are both polynomials since integers are an example of polynomials.
c. \(\frac{x – 1}{x + 1}\) ∙ \(\frac{x + 1}{1}\) = x – 1, and x – 1 is a whole number, not a rational expression.
Answer:
No, he is not correct. \(\frac{x – 1}{x + 1}\)⋅\(\frac{x + 1}{x – 1}\) = \(\frac{x^{2} – 1}{x + 1}\) The numerator and denominator are both polynomials.
d. \(\frac{x – 1}{x + 1}\) ÷ \(\frac{1}{x + 1}\) = x – 1, and x – 1 is a whole number, not a rational expression.
Answer:
No, he is not correct. \(\frac{x – 1}{x + 1}\) ÷ \(\frac{1}{x + 1}\) = \(\frac{x^{2} – 1}{x + 1}\) The numerator and denominator are both polynomials.
Question 2.
Simplify the following rational expressions by rewriting them with a single polynomial denominator.
a. \(\frac{3}{x – 1}\) + \(\frac{2}{x}\)
Answer:
\(\frac{5 x – 2}{x^{2} – x}\)
b. \(\frac{2}{x – 2}\) – \(\frac{3}{x}\)
Answer:
\(\frac{ – x + 6}{x^{2} – 2 x}\)
c. \(\frac{x + 1}{x – 1}\) ∙ \(\frac{x}{x – 1}\)
Answer:
\(\frac{x^{2} + x}{(x – 1)^{2}}\)
d. \(\frac{x + 2}{x – 1}\) ÷ \(\frac{x – 2}{x^{2} – 1}\)
Answer:
\(\frac{x^{2} + 3 x + 2}{x – 2}\)