Engage NY Eureka Math Precalculus Module 3 Lesson 19 Answer Key
Eureka Math Precalculus Module 3 Lesson 19 Exercise Answer Key
Opening Exercise
The function f with domain {1, 2, 3, 4, 5} is shown in the table below.
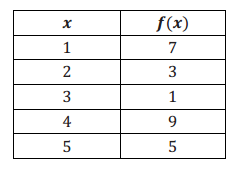
a. What is f(1)? Explain how you know.
Answer:
f(1) = 7 The table shows how the domain values and range values correspond for this function.
b. What is f-1 (1)? Explain how you know.
Answer:
f-1 (1) = 3 Since this is the inverse function, the range values of f are the domain values of f-1.
c. What is the domain of f-1? Explain how you know.
Answer:
The domain of f-1 is the range of f, so the domain of f-1 is the set of numbers {1, 3, 5, 7, 9}.
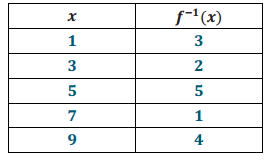
d. Construct a table for the function f-1, the inverse of f.
Answer:
Exercises
Exercise 1.
Complete the mapping diagram to show that f(f-1(x)) = x.
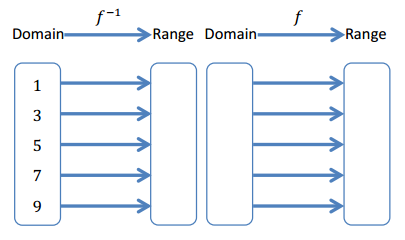
Answer:
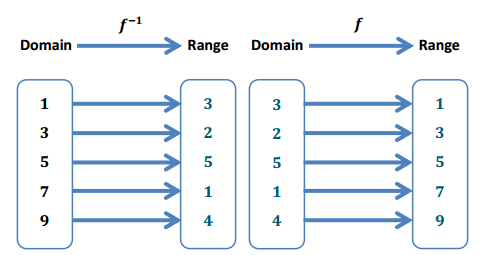
Exercise 2.
Complete the mapping diagram to show that f-1(f(x)) = x.
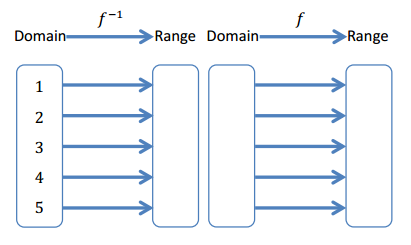
Answer:
Exercise 3.
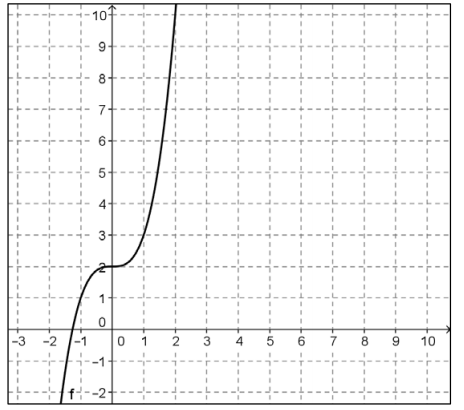
The graph of f is shown below.
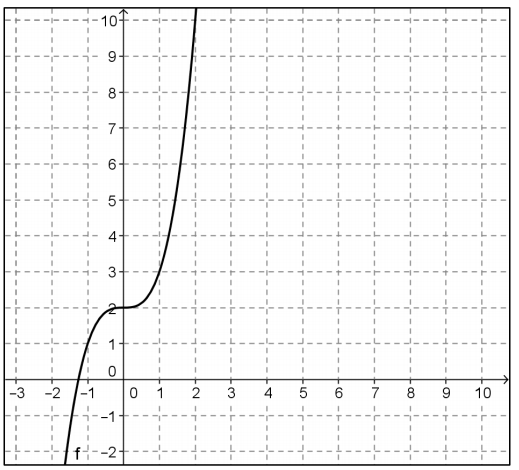
a. Select several ordered pairs on the graph of f, and use those to construct a graph of f-1 in part b.
Answer:
( – 1, 1), (0, 2), (1, 3), (2, 10)
b. Draw the line y = x, and use it to construct the graph of f-1 below.
Answer:
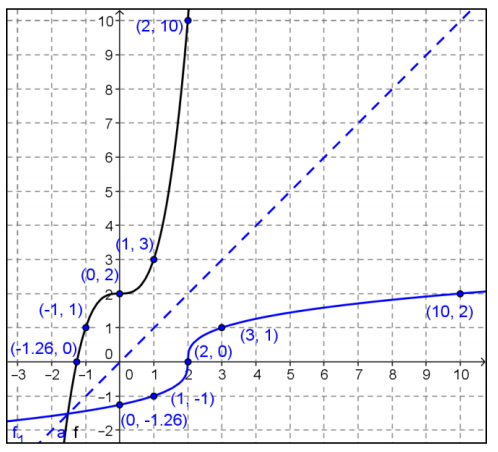
c. The algebraic function for f is given by f(x) = x3 + 2. Is the formula for f-1(x) = \(\sqrt[3]{x – 2}\)? Explain why or why not.
Answer:
No. The formula for f-1is not correct because you don’t get 0 when you substitute 2 into the formula for f3. The correct formula would be f-1(x) = \(\sqrt[3]{x – 2}\).
Exercise 4.
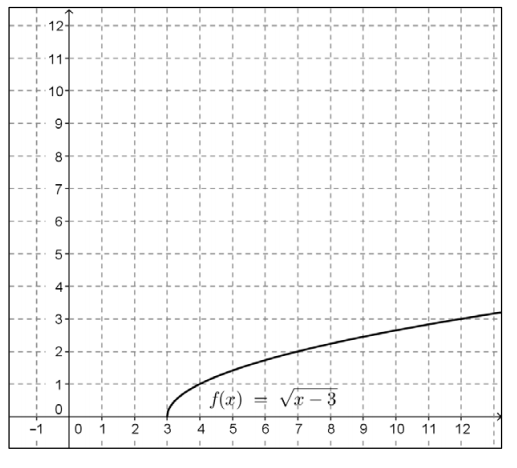
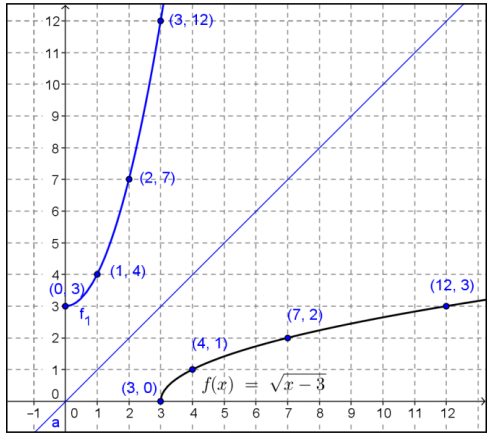
The graph of f(x) = \(\sqrt{x – 3}\) is shown below. Construct the graph of f3.
Answer:
Exercise 5.
Morgan used the procedures learned in Lesson 18 to define f-1(x) = x2 + 3. How does the graph of this function compare to the one you made in Exercise 5?
Answer:
The graph of Morgan’s function, f-1(x) = x2 + 3, is the inverse graph that we drew in Exercise 5. It has a domain that is assumed to be all real numbers. However, the inverse of f must have a domain equal to the range of f, which is f(x) ≥ 0. Thus, the inverse’s domain is not all real numbers but is instead restricted to x ≥ 0. The graphs of these functions are identical for x ≥ 0.
Exercise 6.
Construct the inverse of the function f given by the table below. Is the inverse a function? Explain your reasoning.

Answer:

No, the inverse is not a function. Each element in the domain must have only one element in the range assigned to it. You can see that the number 4 is paired with – 3 and 3.
Exercise 7.
The graphs of several functions are shown below. Which ones are invertible? Explain your reasoning.
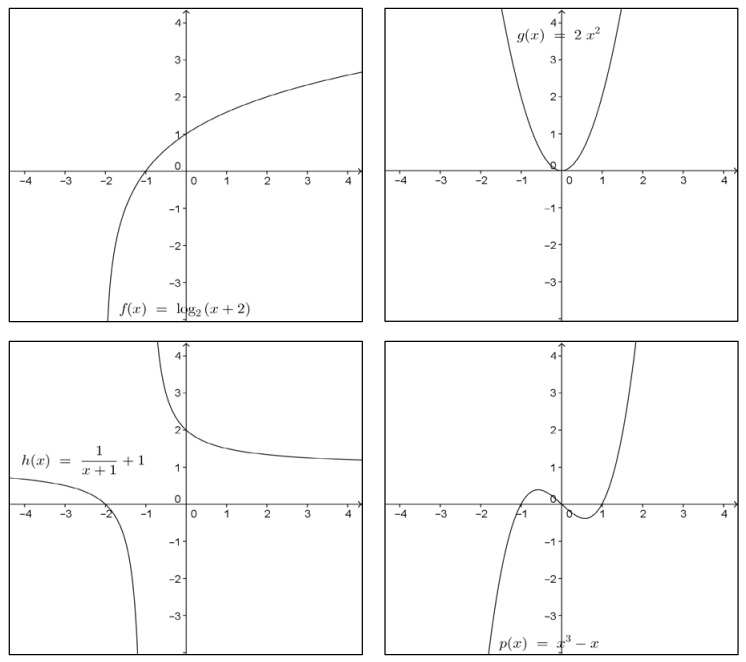
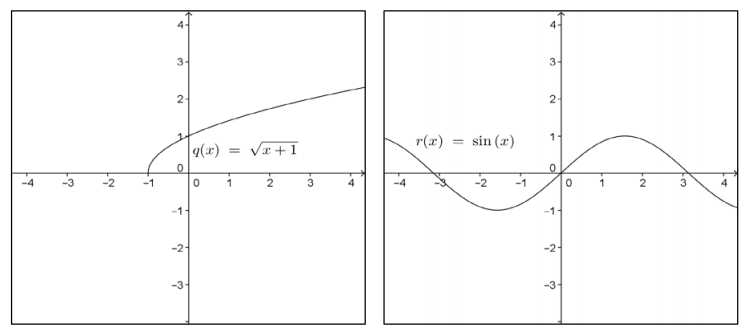
Answer:
The functions g, p, and r are not invertible. You can see that multiple elements of the domain are paired with a single range element. When the domain and range are exchanged to form the inverse, the result does not satisfy the definition of a function.
Exercise 8.
Given the function f(x) = x2 – 4:
a. Select a suitable domain for f that makes it an invertible function. State the range of f.
Answer:
A graph shows that the function f has a minimum point at (0, – 4). One possible domain would start with the x – value of the minimum, x ≥ 0. The range of f given this domain would be f(x) ≥ – 4.
b. Write a formula for f-1. State the domain and range of f-1.
Answer:
Since we know the vertex is (0, – 4), we can rewrite this function in vertex form and then create and solve an equation to find the inverse.
f(x) = x2 – 4
y = x2 – 4
x = y2 – 4
x + 4 = y2
y = \(\sqrt{x + 4}\) or y = – \(\sqrt{x + 4}\)
However, select the positive branch because we want the range to be y ≥ 0.
y = \(\sqrt{x + 4}\), x ≥ – 4
c. Verify graphically that f, with the domain you selected, and f-1 are indeed inverses.
Answer:
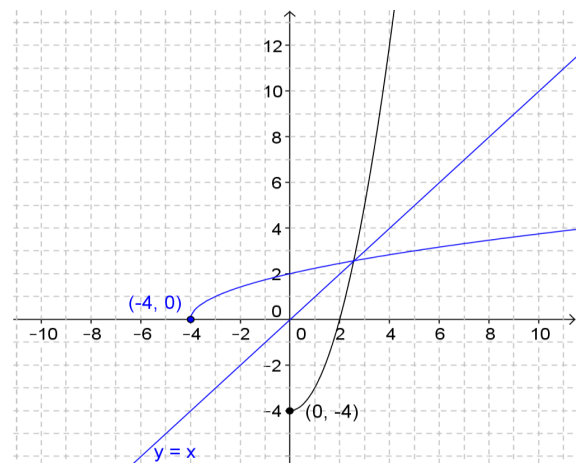
d. Verify that f and f-1 are indeed inverses by showing that f(f-1 (x)) = x and f-1 (f(x)) = x.
Answer:
f(f-1 (x)) = (\(\sqrt{x + 4}\))2 – 4
= x + 4 – 4
= x
f-1 (f(x)) = \(\sqrt{x + 4}\)
= \(\sqrt{x^{2} + 4 – 4}\)
= x, x ≥ 0
Exercise 9.
Three pairs of functions are given below. For which pairs are f and g inverses of each other? Show work to support your reasoning. If a domain is not specified, assume it is the set of real numbers.
a. f(x) = \(\frac{x}{x + 1}\), x≠ – 1 and g(x) = \(\frac{ – x}{x – 1}\), x≠1
Answer:
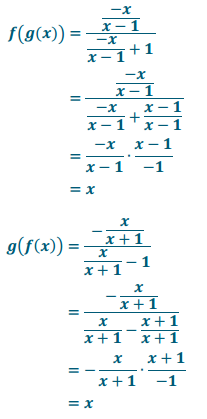
The two functions are inverses.
b. f(x) = \(\sqrt{x}\) – 1, x ≥ 0 and g(x) = (x + 1)2
Answer:
f(g(x)) = \(\sqrt{(x + 1)^{2}}\) – 1 = x + 1 – 1 = x
g(f(x)) = (\(\sqrt{x}\) – 1 + 1)2 = \(\) = x
These two functions are inverses as long as we restrict the domain of g to be x ≥ – 1 since the range of f is f(x) ≥ – 1.
c. f(x) = – 0.75x + 1 and g(x) = – \(\frac{4}{3}\) x – \(\frac{4}{3}\)
Answer:
f(g(x)) = – \(\frac{3}{4}\) ( – \(\frac{4}{3}\) x – \(\frac{4}{3}\)) + 1 = x + 1 + 1 = x + 2
These two functions are not inverses.
Eureka Math Precalculus Module 3 Lesson 19 Problem Set Answer Key
Question 1.
Let f be the function that assigns to each student in the class her biological mother.
a. In order for f to have an inverse, what condition must be true about students in your class?
Answer:
No students in the class can share the same biological mother.
b. If we enlarged the domain to include all students in the school, would this larger domain function have an inverse? Explain.
Answer:
Probably not. Most schools contain siblings.
Question 2.
Consider a linear function of the form f(x) = mx + b, where m and b are real numbers, and m≠0.
a. Explain why linear functions of this form always have an inverse that is also a function.
Answer:
The graphs of these functions are lines. When a line is reflected over the line y = x, the image is also a line and, therefore, can be represented as a linear function.
b. State the general form of a line that does not have an inverse.
Answer:
y = k for some real number k That is, only linear functions whose graphs are horizontal lines do not have inverse functions.
c. What kind of function is the inverse of an invertible linear function (e.g., linear, quadratic, exponential, logarithmic, rational)?
Answer:
The inverse of an invertible linear function would also be a linear function.
d. Find the inverse of a linear function of the form f(x) = mx + b, where m and b are real numbers, and
Answer:
m≠0.
x = my + b
y = \(\frac{x – b}{m}\)
So, f-1(x) = \(\frac{x – b}{m}\) for any linear function f(x) = mx + b, with m≠0.
Question 3.
Consider a quadratic function of the form f(x) = \(b\left(\frac{x – h}{a}\right)^{2} + k\) + k for real numbers a, b, h, k, and a, b≠0.
a. Explain why quadratic functions never have an inverse without restricting the domain.
Every quadratic function is represented by the graph of a parabola, which always reflects over the y = x line in such a way that one input maps to two outputs, violating the definition of a function. Thus, a quadratic function could only have an inverse if its domain is restricted.
b. What are the coordinates of the vertex of the graph of f?
Answer:
(h, k)
c.
State the possible domains you can restrict f on so that it has an inverse.
Answer:
The function f on the domains ( – ∞, h] and [h, ∞) is invertible.
d. What kind of function is the inverse of a quadratic function on an appropriate domain?
Answer:
The inverse of a quadratic function on an appropriate domain is a square root function.
e. Find f-1for each of the domains you gave in part (c).
Answer:
x = \(b\left(\frac{y – h}{a}\right)^{2} + k\)
\(\frac{x – k}{b} = \left(\frac{y – h}{a}\right)^{2}\)
y = \(\pm a \sqrt{\frac{x – k}{b}} + h\)
The inverse function is either described by y = \(a \sqrt{\frac{x – k}{b}} + h\) or y = – \(a \sqrt{\frac{x – k}{b}} + h\) depending on which domain is chosen for f.
Question 4.
Show that f(x) = mx + b for real numbers m and b with m≠0 has an inverse that is also a function.
y = mx + b
x = my + b
x – b = my
\(\frac{1}{m} x – \frac{b}{m}\) = y
Thus, f-1(x) = \(\frac{1}{m} x – \frac{b}{m}\), which is a linear function. One can see from the graph of a line that each input in the domain is paired with one output.
Question 5.
Explain why f(x) = a(x – h)2 + k for real numbers a, h, and k with a≠0 does not have an inverse that is a function. Support your answer in at least two different ways (numerically, algebraically, or graphically).
Answer:
y = a(x – h)2 + k
x = a(y – h)2 + k
\(\frac{x – k}{a}\) = (y – h)2
This equation has two solutions when you take the square root:
y – h = \(\sqrt{\frac{x – k}{a}}\) or y – h = – \(\sqrt{\frac{x – k}{a}}\)
You can see that selecting a single value for x results in two corresponding values of y for all x≠k. Thus, the inverse is not a function.
Graphically, the graph of f is a quadratic function with a vertex at (h, k). The symmetry of this graph means that there are two domain values with the same range value for all x≠h. When the graph of this function is reflected over the line y = x, the resulting graph does not meet the definition of a function.
Extension:
Question 6.
Consider the function f(x) = sin(x).
a. Graph y = f(x) on the domain [ – 2π, 2π].
Answer:
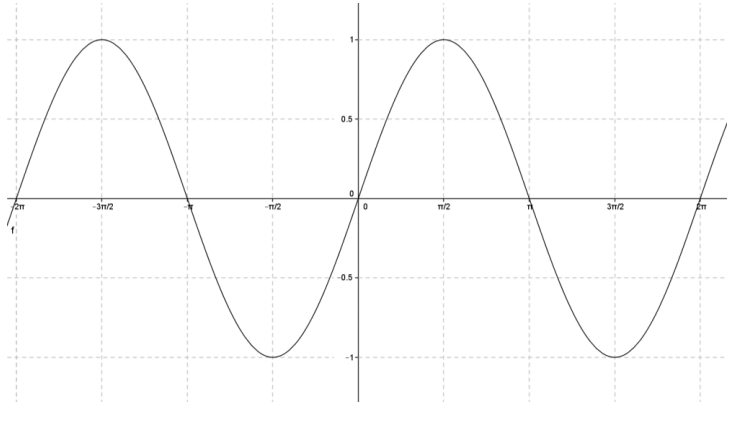
b. If we require a restricted domain on f to be continuous and cover the entirety of the range of f, how many possible choices for a domain are there in your graph from part (a)? What are they?
Answer:
There are three possible choices: [ – \(\frac{3\pi}{2}\), – \(\frac{\pi}{2}\)], [ – \(\frac{\pi}{2}\), \(\frac{\pi}{2}\)], [\(\frac{\pi}{2}\), \(\frac{3\pi}{2}\)].
c. Make a decision on which restricted domain you listed in part (b) makes the most sense to choose. Explain your decision.
Answer:
Answers may vary, but it is expected most students choose [ – \(\frac{\pi}{2}\), \(\frac{\pi}{2}\)] since it includes the origin.
d. Use a calculator to evaluate sin-1(0.75) to three decimal places. How can you use your answer to find other values ψ such that sin(ψ) = 1? Verify that your technique works by checking it against your graph in
part (a).
Answer:
sin-1(0.75) ≈ 0.848
On the unit circle, sine values are equal for supplementary angles of rotation, so π – 0.848 gives another approximate result. Infinitely many values can be found from these two values by adding integer multiples of 2π to either value.
Eureka Math Precalculus Module 3 Lesson 19 Exit Ticket Answer Key
Question 1.
Let f(x) = x2 – 3x + 2.
a. Give a restricted domain for f where it is invertible.
Answer:
The vertex of this parabola is at x = \(\frac{3}{2}\), so either ( – ∞, \(\frac{3}{2}\)] or [\(\frac{3}{2}\), ∞) would be acceptable. The remaining answers assume [\(\frac{3}{2}\), ∞) was chosen.
b. Find the inverse of f for the domain you gave in part (a).
Answer:
f(x) = (x – 1.5)2 – 0.25
x = (y – 1.5)2 – 0.25
y = ±\(\sqrt{x + 0.25}\) + 1.5
For f(x) on the domain [\(\frac{3}{2}\), ∞), f-1(x) = \(\sqrt{x + 0.25}\) + 1.5.
c. State the domain and range of the function you found in part (b).
Answer:
For f-1, the domain is all real numbers greater than or equal to – 0.25, and the range is all real numbers greater than or equal to 1.5.
d. Verify through function composition that the function you found in part (b) is the inverse of f.
Answer:
For x ≥ – 0.25, we have:
f(f-1 (x)) = f(\(\sqrt{x + 0.25}\) + 1.5)
= (\(\sqrt{x + 0.25}\) + 1.5)2 – 3(\(\sqrt{x + 0.25}\) + 1.5) + 2
= x + 0.25 + 3\(\sqrt{x + 0.25}\) + 2.25 – 3\(\sqrt{x + 0.25}\) – 4.5 + 2
= x
For x ≥ 1.5, we have:
f-1 (f(x)) = f-1(x2 – 3x + 2)
= \(\sqrt{x^{2} – 3 x + 2 + 0.25} + 1.5\)
= \(\sqrt{x^{2} – 3 x + \frac{9}{4}} + \frac{3}{2}\)
= \(\sqrt{\left(x – \frac{3}{2}\right)^{2}} + \frac{3}{2}\)
= \(x – \frac{3}{2} + \frac{3}{2}\)
= x
Thus, f(f-1 (x)) = f-1 (f(x)) = x.
e. Graph both functions on the domains specified.
Answer:
Answer: