Engage NY Eureka Math Precalculus Module 2 Lesson 8 Answer Key
Eureka Math Precalculus Module 2 Lesson 8 Exercise Answer Key
Opening Exercise
Compute the product AB for the following pairs of matrices.
a. A=\(\left[\begin{array}{cc}
0 & -1 \\
1 & 0
\end{array}\right]\), B=\(\left[\begin{array}{cc}
0 & -1 \\
1 & 0
\end{array}\right]\)
Answer:
AB=\(\left[\begin{array}{cc}
-1 & 0 \\
0 & -1
\end{array}\right]\)
b. A=\(\left[\begin{array}{cc}
1 & 0 \\
0 & -1
\end{array}\right]\), B=\(\left[\begin{array}{cc}
-1 & 0 \\
0 & 1
\end{array}\right]\)
Answer:
AB=\(\left[\begin{array}{cc}
-1 & 0 \\
0 & -1
\end{array}\right]\)
c. 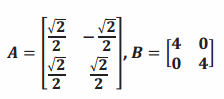
Answer:
AB=\(\left[\begin{array}{cc}
2 \sqrt{2} & -2 \sqrt{2} \\
2 \sqrt{2} & 2 \sqrt{2}
\end{array}\right]\)
d. A=\(\left[\begin{array}{ll}
1 & 1 \\
0 & 1
\end{array}\right]\), B=\(\left[\begin{array}{ll}
2 & 0 \\
0 & 2
\end{array}\right]\)
Answer:
AB=\(\left[\begin{array}{ll}
2 & 2 \\
0 & 2
\end{array}\right]\)
e. 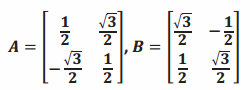
Answer:
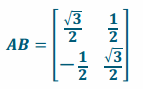
Eureka Math Precalculus Module 2 Lesson 8 Exploratory Challenge Answer Key
Exploratory Challenge
For each pair of matrices A and B given below:
1. Describe the geometric effect of the transformation LB\(\left(\left[\begin{array}{l}
x \\
y
\end{array}\right]\right)\)=B⋅\(\left(\left[\begin{array}{l}
x \\
y
\end{array}\right]\right)\).
2. Describe the geometric effect of the transformation LA\(\left[\begin{array}{l}
x \\
y
\end{array}\right]\)=A⋅\(\left[\begin{array}{l}
x \\
y
\end{array}\right]\).
3. Draw the image of the unit square under the transformation LB\(\left[\begin{array}{l}
x \\
y
\end{array}\right]\)=B⋅\(\left[\begin{array}{l}
x \\
y
\end{array}\right]\).
4. Draw the image of the transformed square under the transformation LA\(\left[\begin{array}{l}
x \\
y
\end{array}\right]\)=A⋅\(\left[\begin{array}{l}
x \\
y
\end{array}\right]\).
5. Describe the geometric effect on the unit square of performing first LBand then LA.
6. Compute the matrix product AB.
7. Describe the geometric effect of the transformation LAB \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\)=AB⋅\(\left[\begin{array}{l}
x \\
y
\end{array}\right]\).
i. A=\(\left[\begin{array}{cc}
0 & -1 \\
1 & 0
\end{array}\right]\), B=\(\left[\begin{array}{cc}
0 & -1 \\
1 & 0
\end{array}\right]\)
1. The transformation produced by matrix B has the effect of rotation by 90° counterclockwise.
2. The transformation produced by matrix A has the effect of rotation by 90° counterclockwise.
3. The green square in the second quadrant is the image of the original square under the transformation produced by B.
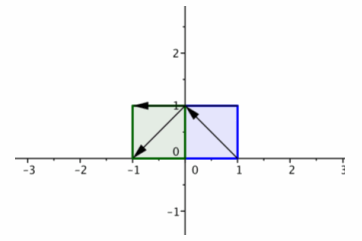
4. The red square in the third quadrant is the image of the square after transforming with matrix A and then matrix B.
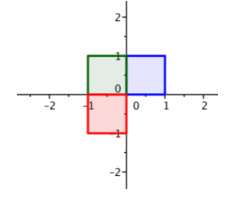
5. If we rotate twice by 90°, then the net effect is a rotation by 180°.
6. The matrix product is AB=\(\left[\begin{array}{cc}
-1 & 0 \\
0 & -1
\end{array}\right]\).
7. The transformation produced by matrix AB has the effect of rotation by 180°.
ii. A=\(\left[\begin{array}{cc}
1 & 0 \\
0 & -1
\end{array}\right]\), B=\(\left[\begin{array}{cc}
-1 & 0 \\
0 & 1
\end{array}\right]\)
Answer:
1. The transformation produced by matrix B has the effect of reflection across the y-axis.
2. The transformation produced by matrix A has the effect of reflection across the x-axis.
3. The green square in the second quadrant is the image of the original square under the transformation produced by B.
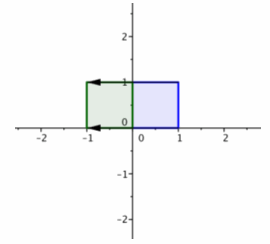
4. The red square in the third quadrant is the image of the square after transforming with matrix A and then matrix B.
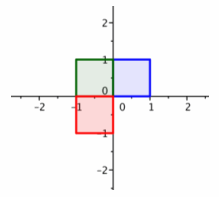
5. If we reflect across the y-axis and then reflect across the x-axis, the net effect is a rotation by 180°.
6. The matrix product is AB=\(\left[\begin{array}{cc}
-1 & 0 \\
0 & -1
\end{array}\right]\).
7. The transformation produced by matrix AB has the effect of rotation by 180°.
iii. 
Answer:
1. The transformation produced by matrix B has the effect of dilation from the origin with scale factor 4.
2. The transformation produced by matrix A has the effect of rotation by 45°.
3. The large green square is the image of the original unit square under the transformation produced by B.
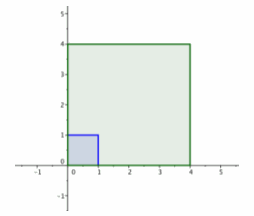
4. The tilted red square is the image of the green square under the transformation produced by A.
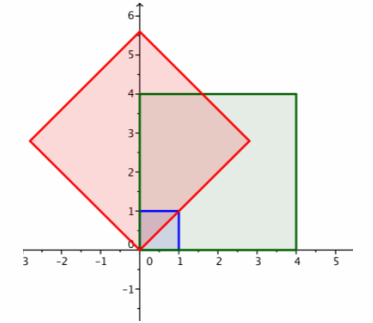
5. If we dilate with factor 4 and then rotate by 45°, the net effect is a rotation by 45° and dilation with scale factor 4.
6. The matrix product is AB=\(\left[\begin{array}{cc}
2 \sqrt{2} & -2 \sqrt{2} \\
2 \sqrt{2} & 2 \sqrt{2}
\end{array}\right]\).
7. The transformation produced by matrix AB has the effect of rotation by 45° while scaling by 4.
iv. A=\(\left[\begin{array}{ll}
1 & 1 \\
0 & 1
\end{array}\right]\), B=\(\left[\begin{array}{ll}
2 & 0 \\
0 & 2
\end{array}\right]\)
Answer:
1. The transformation produced by matrix B has the effect of dilation with scale factor 2.
2. The transformation produced by matrix A has the effect of shearing parallel to the y-axis.
3. The large green square is the image of the original unit square under the transformation produced by B.
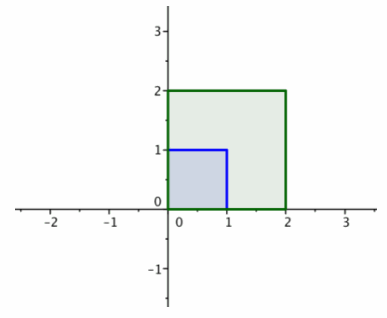
4. The red parallelogram is the image of the green square under the transformation produced by A.
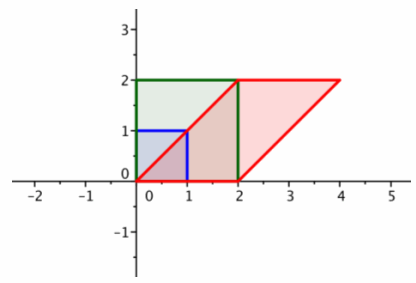
5. If we dilate and then shear, the net effect is a dilated shear.
6. The matrix product is AB=\(\left[\begin{array}{ll}
2 & 2 \\
0 & 2
\end{array}\right]\).
7. The transformation produced by matrix AB has the effect of a dilated shear.
v. 
Answer:
1. The transformation produced by matrix B has the effect of rotation by 30°.
2. The transformation produced by matrix A has the effect of rotation by -60°.
3. The tilted green square is the image of the original unit square under the transformation produced by B.
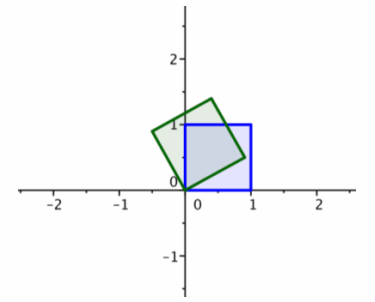
4. The tilted red square is the image of the green square under the transformation produced by A.
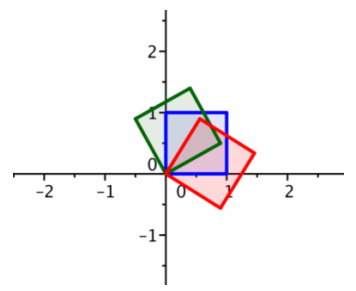
5. If we rotate by 30° counterclockwise and then rotate by 60° clockwise, the net result is a rotation by 30° counterclockwise.
6. The matrix product is AB=\(\left[\begin{array}{cc}
\frac{\sqrt{3}}{2} & \frac{1}{2} \\
-\frac{1}{2} & \frac{\sqrt{3}}{2}
\end{array}\right]\).
7. The transformation produced by matrix AB has the effect of rotation by -30°.
b. Make a conjecture about the geometric effect of the linear transformation produced by the matrix AB. Justify your answer.
Answer:
The linear transformation produced by matrix AB has the same geometric effect of the sequence of the linear transformation produced by matrix B followed by the linear transformation produced by matrix A. We have seen in previous work that if we multiply by AB, we get the same transformation as when we multiplied by A first and then multiplied the result by B.
Eureka Math Precalculus Module 2 Lesson 8 Problem Set Answer Key
Question 1.
Let A be the matrix representing a dilation of \(\frac{1}{2}\), and let B be the matrix representing a reflection across the y-axis.
a. Write A and B.
Answer:
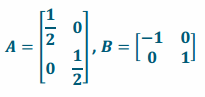
b. Evaluate AB. What does this matrix represent?
Answer:
AB=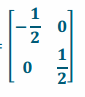
AB is a reflection across the y-axis followed by a dilation of \(\frac{1}{2}\).
c. Let x=\(\left[\begin{array}{l}
5 \\
6
\end{array}\right]\), y=\(\left[\begin{array}{l}
-1 \\
3
\end{array}\right]\), and z=\(\left[\begin{array}{l}
8 \\
-2
\end{array}\right]\). Find (AB)x, (AB)y, and (AB)z.
Answer:
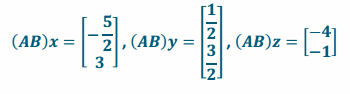
Question 2.
Let A be the matrix representing a rotation of 30°, and let B be the matrix representing a dilation of 5.
a. Write A and B.
Answer:
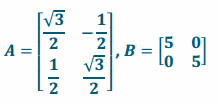
b. Evaluate AB. What does this matrix represent?
Answer:
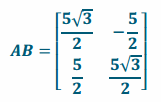
AB is a dilation of 5 followed by a rotation of 30°.
c. Let x=\(\left[\begin{array}{l}
1 \\
0
\end{array}\right]\). Find (AB)x.
Answer:
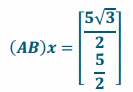
Question 3.
Let A be the matrix representing a dilation of 3, and let B be the matrix representing a reflection across the line y=x.
a. Write A and B.
Answer:
A=\(\left[\begin{array}{ll}
3 & 0 \\
0 & 3
\end{array}\right]\), B=\(\left[\begin{array}{ll}
0 & 1 \\
1 & 0
\end{array}\right]\)
b. Evaluate AB. What does this matrix represent?
Answer:
AB=\(\left[\begin{array}{ll}
0 & 3 \\
3 & 0
\end{array}\right]\)
AB is a reflection across the line y=x followed by a dilation of 3.
c. Let x=\(\left[\begin{array}{c}
-2 \\
7
\end{array}\right]\). Find (AB)x.
Answer:
(AB)x=\(\left[\begin{array}{c}
21 \\
-6
\end{array}\right]\)
Question 4
Let A=\(\left[\begin{array}{ll}
3 & 0 \\
3 & 3
\end{array}\right]\) and B=\(\left[\begin{array}{cc}
0 & -1 \\
1 & 0
\end{array}\right]\).
a. Evaluate AB.
Answer:
\(\left[\begin{array}{ll}
0 & -3 \\
3 & -3
\end{array}\right]\)
b. Let x=\(\left[\begin{array}{c}
-2 \\
2
\end{array}\right]\). Find (AB)x.
Answer:
\(\left[\begin{array}{c}
-6 \\
-12
\end{array}\right]\)
c. Graph x and (AB)x.
Answer:
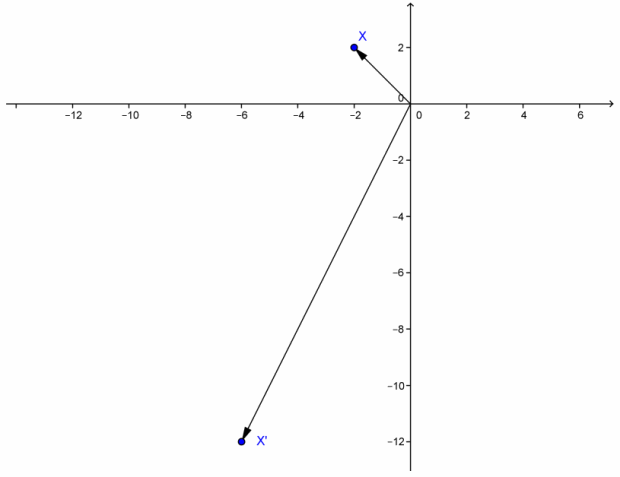
Question 5.
Let A=\(\left[\begin{array}{ll}
\frac{1}{3} & 0 \\
2 & \frac{1}{3}
\end{array}\right]\) and B=\(\left[\begin{array}{cc}
3 & 1 \\
1 & -3
\end{array}\right]\).
a. Evaluate AB.
Answer:
\(\left[\begin{array}{cc}
1 & \frac{1}{3} \\
\frac{19}{3} & 1
\end{array}\right]\)
b. Let x=\(\left[\begin{array}{l}
0 \\
3
\end{array}\right]\). Find (AB)x.
Answer:
\(\left[\begin{array}{l}
1 \\
3
\end{array}\right]\)
c. Graph x and (AB)x.
Answer:
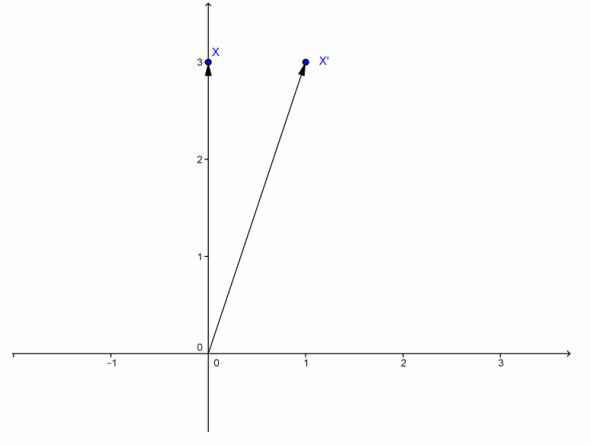
Question 6.
Let A=\(\left[\begin{array}{ll}
2 & 2 \\
2 & 0
\end{array}\right]\) and B=\(\left[\begin{array}{ll}
0 & 2 \\
2 & 2
\end{array}\right]\).
a. Evaluate AB.
Answer:
\(\left[\begin{array}{ll}
4 & 8 \\
0 & 4
\end{array}\right]\)
b. Let x=\(\left[\begin{array}{c}
3 \\
-2
\end{array}\right]\). Find (AB)x.
Answer:
\(\left[\begin{array}{l}
-4 \\
-8
\end{array}\right]\)
c. Graph x and (AB)x.
Answer:
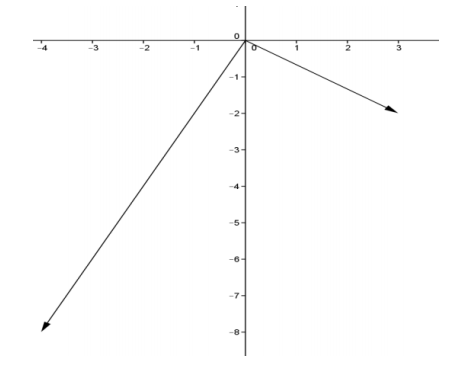
Question 7.
Let A, B, C be 2×2 matrices representing linear transformations.
a. What does A(BC) represent?
Answer:
A(BC) represents the linear transformation of applying the transformation that C represents, followed by the transformation that B represents, followed by the transformation that A represents.
b. Will the pattern established in part (a) be true no matter how many matrices are multiplied on the left?
Answer:
Yes, in general. When you multiply by a matrix on the left, you are applying a linear transformation after all linear transformations to the right have been applied.
c. Does (AB)C represent something different from A(BC)? Explain.
Answer:
No, it does not. This is the linear transformation obtained by applying C and then AB, which is B followed by A.
Question 8.
Let AB represent any composition of linear transformations in R2. What is the value of (AB)x where x=\(\left[\begin{array}{l}
\mathbf{0} \\
\mathbf{0}
\end{array}\right]\)?
Answer:
Since a composition of linear transformations in R2 is also a linear transformation, we know that applying it to the origin will result in no change.
Eureka Math Precalculus Module 2 Lesson 8 Exit Ticket Answer Key
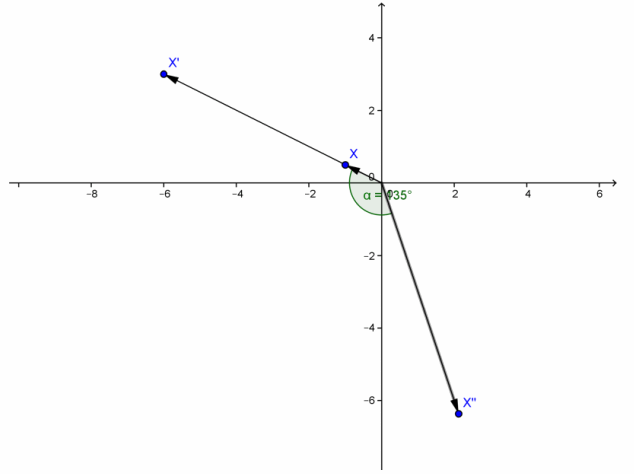
Let A be the matrix representing a rotation about the origin 135° and B be the matrix representing a dilation of 6. Let x=\(\left[\begin{array}{c}
-1 \\
\frac{1}{2}
\end{array}\right]\).
a. Write down A and B.
Answer:
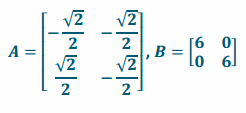
b. Find the matrix representing a dilation x by 6, followed by a rotation about the origin of 135°.
Answer:
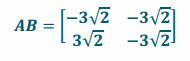
c. Graph and label x, x after a dilation of 6, and x after both transformations have been applied.
Answer: