Eureka Math Precalculus Module 2 Lesson 7 Answer Key

Engage NY Eureka Math Precalculus Module 2 Lesson 7 Answer Key

Eureka Math Precalculus Module 2 Lesson 7 Exercise Answer Key

Opening Exercise

Consider the following matrices: A=\(\left[\begin{array}{ll}
1 & 2 \\
2 & 4
\end{array}\right]\), B=\(\left[\begin{array}{ll}
2 & 0 \\
0 & 0
\end{array}\right]\), and C=\(\left[\begin{array}{cc}
2 & -2 \\
2 & 2
\end{array}\right]\)
a. Compute the following determinants.
i. det(A)
Answer:
det(A)=4-4=0

ii. det(B)
Answer:
det(B)=0-0=0

iii. det(C)
Answer:
det(C)=4-(-4)=8

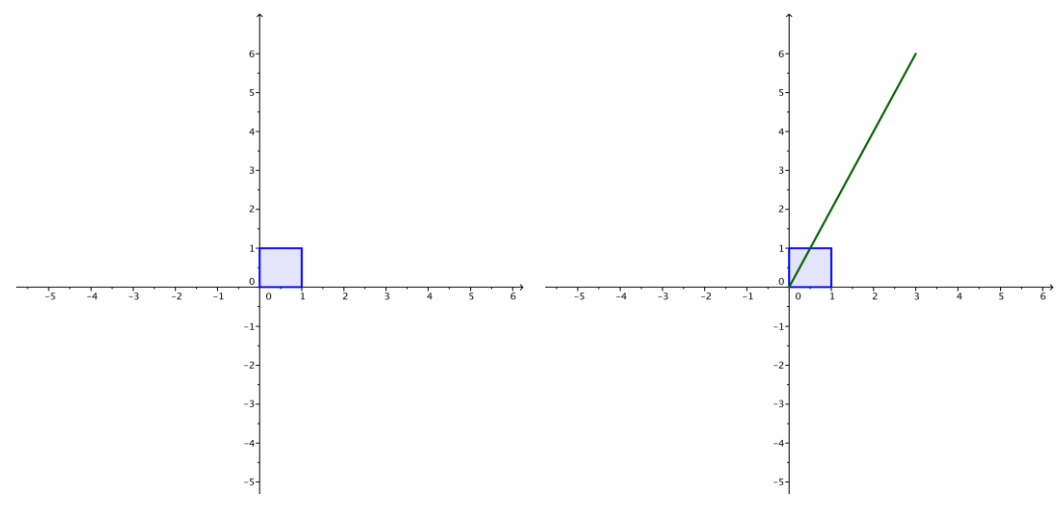
b. Sketch the image of the unit square after being transformed by each transformation.
i. L_A\(\left(\left[\begin{array}{l}
x \\
y
\end{array}\right]\right)\)=\(\left[\begin{array}{ll}
1 & 2 \\
2 & 4
\end{array}\right]\left[\begin{array}{l}
x \\
y
\end{array}\right]\)
Answer:

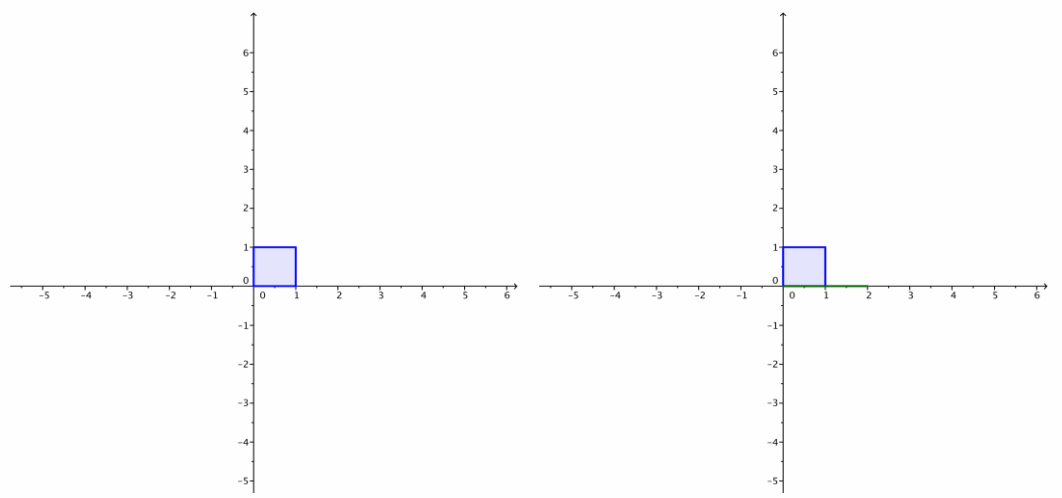
ii. L_B\(\left(\left[\begin{array}{l}
x \\
y
\end{array}\right]\right)\)=\(\left[\begin{array}{ll}
2 & 0 \\
0 & 0
\end{array}\right]\left[\begin{array}{l}
x \\
y
\end{array}\right]\)
Answer:

iii. L_C\(\left(\left[\begin{array}{l}
x \\
y
\end{array}\right]\right)\)=\(\left[\begin{array}{cc}
2 & -2 \\
2 & 2
\end{array}\right]\left[\begin{array}{l}
x \\
y
\end{array}\right]\)
Answer:

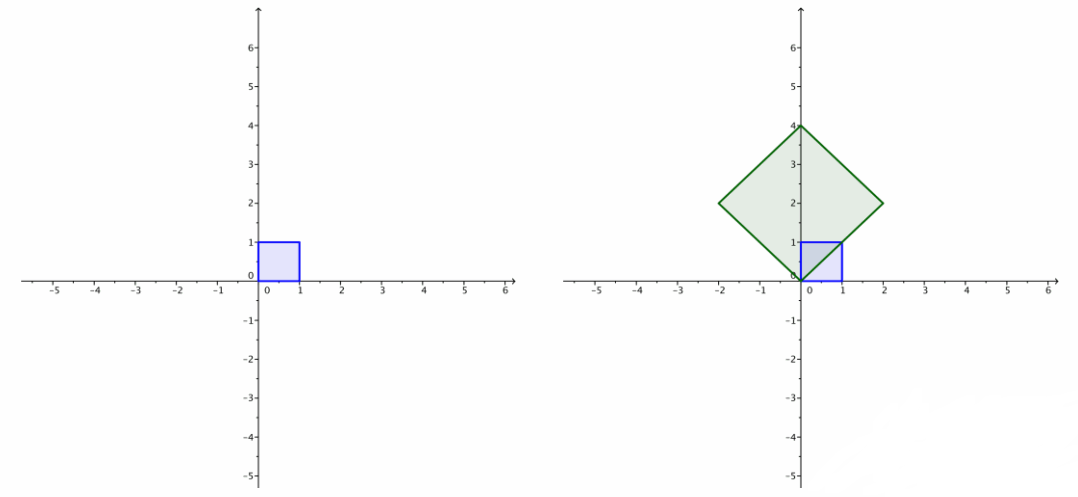
c. Find the area of each image of the unit square in Part b.
Answer:
The first two have no area because each image is a line segment. The third one is a square with sides of length \(2 \sqrt{2}\), so its area is (\(2 \sqrt{2}\))²=8.

d. Explain the connection between the responses to Parts a and b.
Answer:
The determinant of the matrix A is the area of the image of the unit square under the transformation induced by A.

Eureka Math Precalculus Module 2 Lesson 7 Exploratory Challenge Answer Key

Exploratory Challenge 1
For each matrix A given below:
i. Plot the image of the unit cube under the transformation.
ii. Find the volume of the image of the unit cube from part (i).
iii. Does the transformation have an inverse? If so, what is the matrix that induces the inverse transformation?
a. A=\(\left[\begin{array}{lll}
2 & 0 & 0 \\
0 & 2 & 0 \\
0 & 0 & 2
\end{array}\right]\)
Answer:
i.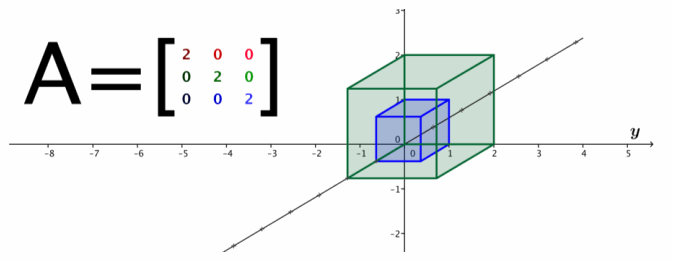
ii. The image of the unit cube is a cube with sides of length 2. Thus, the volume of the image of the unit cube is 2 ⋅ 2 ⋅ 2=8.
iii. This transformation has an inverse. To undo dilation by 2, we need to dilate by \(\frac{1}{2}\). The matrix that represents the inverse transformation is B=\(\left[\begin{array}{lll}
\frac{1}{2} & 0 & 0 \\
0 & \frac{1}{2} & 0 \\
0 & 0 & \frac{1}{2}
\end{array}\right] .\)

b. A=\(\left[\begin{array}{ccc}
4 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & -2
\end{array}\right]\)
Answer:
i.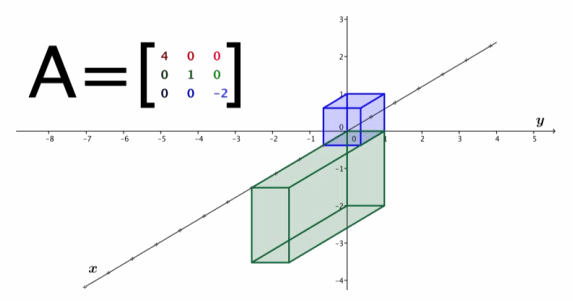
ii. The image of the unit cube is a box with sides of length 4, 1, and 2. Thus, the volume of the image of the unit cube is 4⋅1⋅2=8.
iii. This transformation is also invertible. To undo this transformation, we need to scale by \(\frac{1}{4}\) in the
x-direction, by 1 in the y-direction, and by –\(\frac{1}{2}\) in the z-direction. The matrix that will induce this inverse transformation is B=\(\left[\begin{array}{ccc}
\frac{1}{4} & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & -\frac{1}{2}
\end{array}\right]\).

c. \(\left[\begin{array}{ccc}
4 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & -2
\end{array}\right]\)
Answer:
i.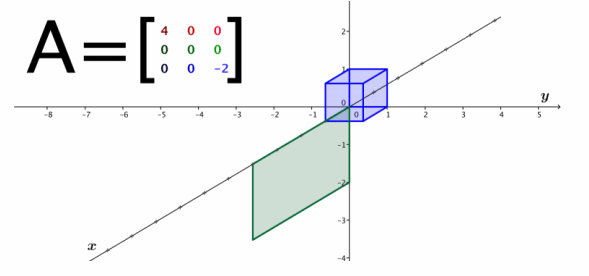
ii. The image of the unit cube is a rectangle with sides of length 2 and 4. Thus, the volume of the image of the unit cube is 4⋅0⋅2=0.
iii. This transformation is not invertible since the image was collapsed from a cube onto a rectangle. Many points get sent to the same point on the rectangle, so we cannot undo the transformation in a clear way.

d. Describe the geometric effect of a transformation 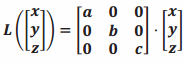for numbers a, b, and c. Describe when such a transformation is invertible.
Answer:
The transformation L scales the side of the cube along the x-axis by a, the side of the cube along the y-axis by b, and the side of the cube along the z-axis by c. If any of the numbers a, b, and c are zero, then the image is no longer a three-dimensional figure, so the transformation will not be invertible. Thus, the transformation is invertible only when a≠0, b≠0, and c≠0.

Exploratory Challenge 2.

a. Make a prediction: What would be the geometric effect of the transformation
on the unit cube? Use the GeoGebra demo to test your conjecture.
Answer:

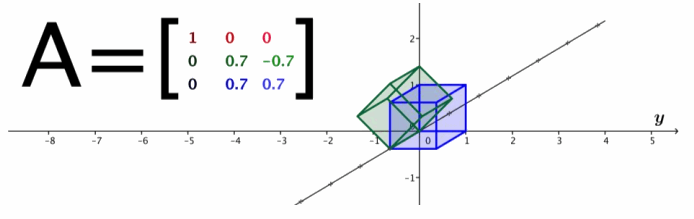
Students should recognize that this transformation should have something to do with rotation. However, they most likely need to see the resulting image before identifying it as rotation by 45° about the x-axis.

b. For each geometric transformation below, find a matrix A so that the geometric effect of 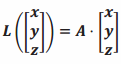is the specified transformation.
i. Rotation by -45° about the x-axis
Answer:

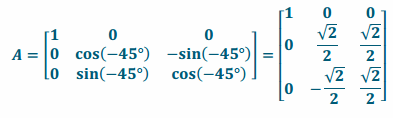
ii. Rotation by 45° about the y-axis
Answer:

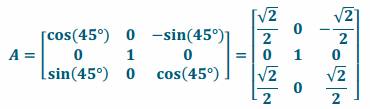
iii. Rotation by 45° about the z-axis
Answer:

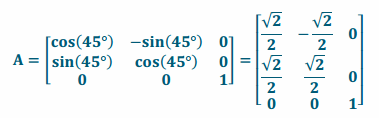
iv. Rotation by 90° about the x-axis
Answer:

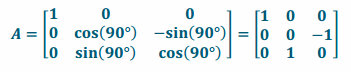
v. Rotation by 90° about the y-axis
Answer:

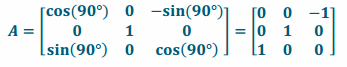
vi. Rotation by 90° about the z-axis
Answer:

vii. Rotation by θ about the x-axis
Answer:

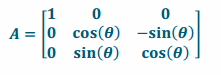
viii. Rotation by θ about the y-axis
Answer:

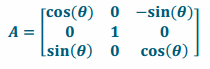
viii. Rotation by θ about the z-axis
Answer:

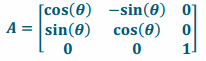
Exploratory Challenge 3.
Describe the geometric effect of each transformation 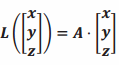for the given matrices A. Be as specific as you can.
a. A=\(\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 0 & 1 \\
0 & 1 & 0
\end{array}\right]\)

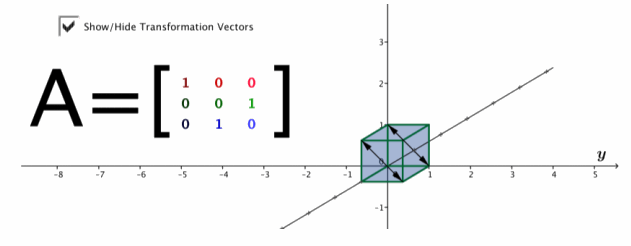
Answer:
The images of the two cubes coincide; this transformation reflects across the plane through the points (1,0,0), (1,1,1), (0,1,1), and (0,0,0).

b. A=\(\left[\begin{array}{lll}
2 & 1 & 0 \\
2 & 1 & 0 \\
2 & 1 & 0
\end{array}\right]\)

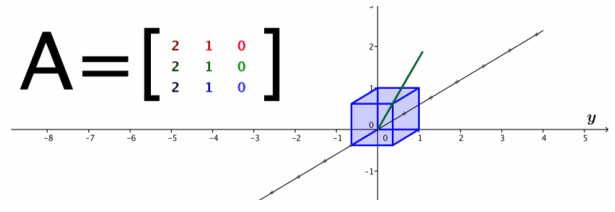
Answer:
This transformation collapses the cube onto a line segment from (0,0,0) to (3,3,3).

c. A=\(\left[\begin{array}{ccc}
2 & 2 & 0 \\
-2 & 2 & 0 \\
0 & 0 & 1
\end{array}\right]\)

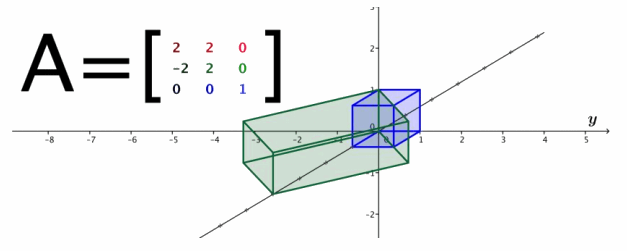
Answer:
This transformation stretches the cube in the x and y directions and then rotates by -45°.

Eureka Math Precalculus Module 2 Lesson 7 Problem Set Answer Key

Problems 1 and 2 continue to develop the theory of linear transformations represented by matrix multiplication. Problem 3 can be done with or without access to the GeoGebra demo used in the lesson.

Question 1.
Suppose that we have a linear transformation 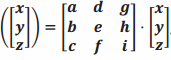for some matrix A = \(\left[\begin{array}{lll}
a & d & g \\
b & e & h \\
c & f & i
\end{array}\right]\).
a. Evaluate L\(\left(\left[\begin{array}{l}
1 \\
0 \\
0
\end{array}\right]\right)\). How does the result relate to the matrix A?
Answer:
L\(\left(\left[\begin{array}{l}
1 \\
0 \\
0
\end{array}\right]\right)\)=\(\left[\begin{array}{l}
a \\
b \\
c
\end{array}\right]\) It is the first column of matrix A.

b. Evaluate L\(\left(\left[\begin{array}{l}
0 \\
1 \\
0
\end{array}\right]\right)\). How does the result relate to the matrix A?
Answer:
L\(\left(\left[\begin{array}{l}
0 \\
1 \\
0
\end{array}\right]\right)\)=\(\left[\begin{array}{l}
d \\
e \\
f
\end{array}\right]\) It is the second column of matrix A.

c. Evaluate L\(\left(\begin{array}{l}
\left.\left[\begin{array}{l}
0 \\
0 \\
1
\end{array}\right]\right)
\end{array}\right.\). How does the result relate to the matrix A?
Answer:
L\(\left(\left[\begin{array}{l}
0 \\
0 \\
1
\end{array}\right]\right)\)=\(\left[\begin{array}{c}
g \\
h \\
i
\end{array}\right]\) It is the third column of matrix A.

d. James correctly said that if you know what a linear transformation does to the three points (1,0,0), (0,1,0), and (0,0,1), you can find the matrix of the transformation. Explain how you can find the matrix of the transformation given the image of these three points.
Answer:
Create a matrix with L(\(\left(\left[\begin{array}{l}
1 \\
0 \\
0
\end{array}\right]\right)\)) in the first column, L(\(\left(\left[\begin{array}{l}
0 \\
1 \\
0
\end{array}\right]\right)\)) in the second column, and L(\(\left(\left[\begin{array}{l}
0 \\
1 \\
0
\end{array}\right]\right)\)) in the third column.

Question 2.
Use the result from Problem 1(d) to answer the following questions.
a. Suppose a transformation L:R³→R³ satisfies L(\(\left(\left[\begin{array}{l}
1 \\
0 \\
0
\end{array}\right]\right)\))=[\(\left(\left[\begin{array}{l}
3 \\
0 \\
0
\end{array}\right]\right)\), L(\(\left(\left[\begin{array}{l}
0 \\
1 \\
0
\end{array}\right]\right)\))=\(\left(\left[\begin{array}{l}
0 \\
3 \\
0
\end{array}\right]\right)\), and L(\(\left(\left[\begin{array}{l}
0 \\
0 \\
1
\end{array}\right]\right)\))=[\(\left(\left[\begin{array}{l}
0 \\
0 \\
0
\end{array}\right]\right)\).

i. What is the matrix A that represents the transformation L?
Answer:
A=\(\left[\begin{array}{lll}
3 & 0 & 0 \\
0 & 3 & 0 \\
0 & 0 & 3
\end{array}\right]\)

ii. What is the geometric effect of the transformation L?
Answer:
The transformation L has the geometric effect of dilation by a factor of 3.

iii. Sketch the image of the unit cube after the transformation by L.
Answer:

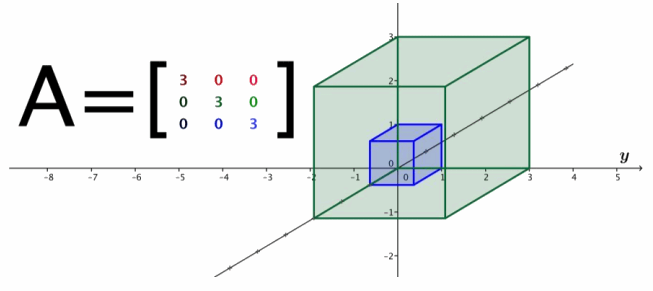
b. Suppose a transformation L:R³→R³ satisfies L(\(\left[\begin{array}{l}
1 \\
0 \\
0
\end{array}\right]\))=\(\left[\begin{array}{l}
1 \\
0 \\
0
\end{array}\right]\), L(\(\left[\begin{array}{l}
0 \\
1 \\
0
\end{array}\right]\))=[\(\left[\begin{array}{l}
0 \\
1 \\
0
\end{array}\right]\), and L(\(\left[\begin{array}{l}
0 \\
0 \\
1
\end{array}\right]\))=[\(\left[\begin{array}{l}
0 \\
0 \\
-4
\end{array}\right]\).

i. What is the matrix A that represents the transformation L?
Answer:
A=\(\left[\begin{array}{ccc}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & -4
\end{array}\right]\)

ii. What is the geometric effect of the transformation L?
Answer:
The transformation L has the geometric effect of stretching by a factor of -4 in the z-direction.

iii. Sketch the image of the unit cube after the transformation by L.
Answer:

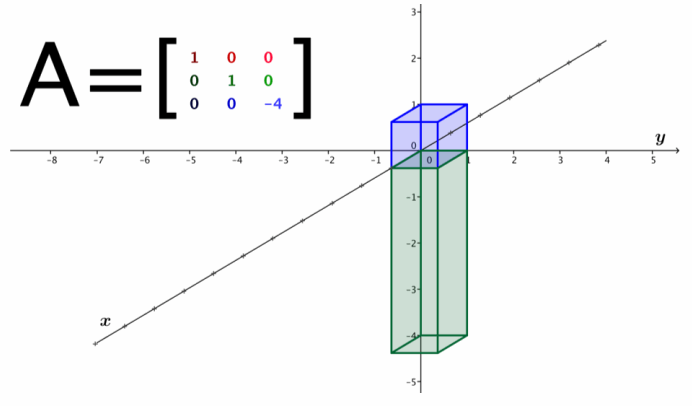
c. Suppose a transformation L:R³→R³ satisfies L\(\left(\left[\begin{array}{l}
1 \\
0 \\
0
\end{array}\right]\right)\)=\(\left(\left[\begin{array}{l}
3 \\
0 \\
0
\end{array}\right]\right)\), L\(\left(\left[\begin{array}{l}
0 \\
1 \\
0
\end{array}\right]\right)\)=\(\left[\begin{array}{l}
0 \\
3 \\
0
\end{array}\right]\), and L\(\left(\begin{array}{l}
\left.\left[\begin{array}{l}
0 \\
0 \\
1
\end{array}\right]\right)
\end{array}\right.\)=\(\left[\begin{array}{l}
0 \\
0 \\
3
\end{array}\right]\).

i. What is the matrix A that represents the transformation L?
Answer:
A=\(\left[\begin{array}{ccc}
-2 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & -2
\end{array}\right]\)

ii. What is the geometric effect of the transformation L?
Answer:
The transformation L has the geometric effect of rotating about the y-axis by 180° and stretching by a factor of 2 in the x and z directions.

iii. Sketch the image of the unit cube after transformation by L.
Answer:

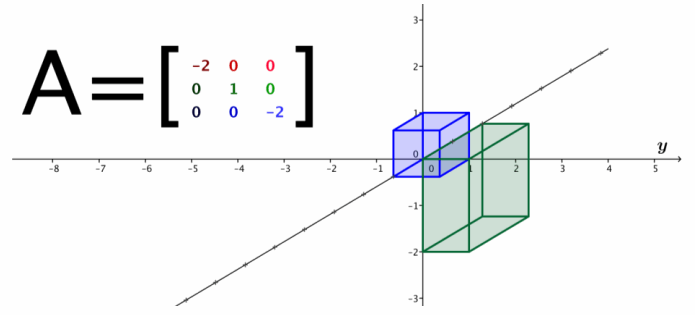
Question 3.
Find the matrix of the transformation that will produce the following images of the unit cube. Describe the geometric effect of the transformation.
a.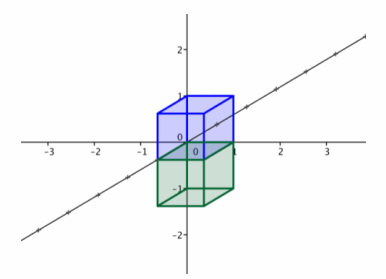
Answer:
The geometric effect of this transformation is reflection across the xy-plane. The matrix that represents this transformation is A=\(\left[\begin{array}{ccc}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & -1
\end{array}\right]\).

b.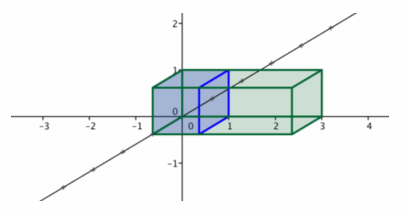
Answer:
The geometric effect of this transformation is a stretch in the y-direction by a factor of 3. The matrix that represents this transformation is A=\(\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 3 & 0 \\
0 & 0 & 1
\end{array}\right]\).

c.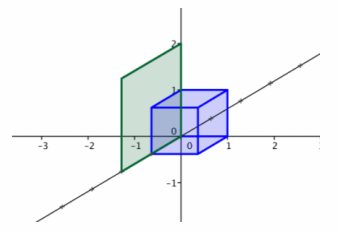
Answer:
The geometric effect of this transformation is a stretch in the x- and z-directions by a factor of 2 and projection onto the xz-plane. The matrix that represents this transformation is A=\(\left[\begin{array}{lll}
2 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 2
\end{array}\right]\).

d.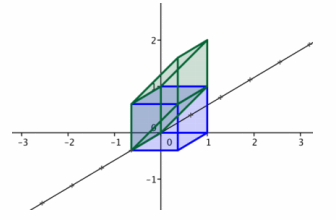
Answer:
The geometric effect of this transformation is a shear parallel to the xz-plane. The matrix that represents this transformation is A=\(\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 1 & 1
\end{array}\right]\).