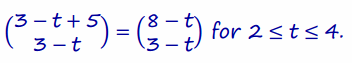Eureka Math Precalculus Module 1 End of Module Assessment Answer Key

Engage NY Eureka Math Precalculus Module 1 End of Module Assessment Answer Key

Eureka Math Precalculus Module 1 End of Module Assessment Task Answer Key

Question 1.
Consider the transformation on the plane given by the 2×2 matrix \(\left(\begin{array}{ll}
1 & k \\
0 & k
\end{array}\right)\) for a fixed positive number k>1.

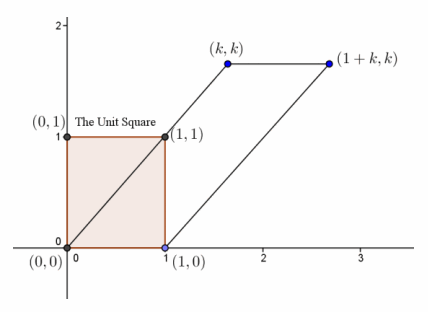
a. Draw a sketch of the image of the unit square under this transformation (the unit square has vertices (0,0), (1,0), (0,1), and (1,1)). Be sure to label all four vertices of the image figure.

Answer:
To find the coordinates of the image, multiply the vertices of the unit square by the matrix.

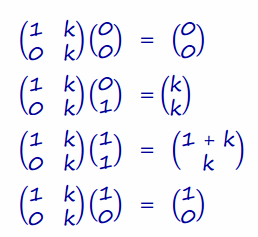
The image is a parallelogram with base = 1 and height = k.

b. What is the area of the image parallelogram?
Answer:
To find the area of the image figure, multiply the area of the unit square by the absolute value of \(\left[\begin{array}{ll}
1 & k \\
0 & k
\end{array}\right]\).
\(\left|\begin{array}{ll}
1 & k \\
0 & k
\end{array}\right|\)=(1 × k)-(0 × k)=k
Area = 1 × |k|= k since k > 0

c. Find the coordinates of a point \(\left(\begin{array}{l}
x \\
y
\end{array}\right)\) whose image under the transformation is \(\left(\begin{array}{l}
2 \\
3
\end{array}\right)\).
Answer:
Solve the equation to find the coordinates of \(\left(\begin{array}{l}
x \\
y
\end{array}\right)\).
\(\left(\begin{array}{ll}
1 & k \\
0 & k
\end{array}\right)\left(\begin{array}{l}
x \\
y
\end{array}\right)\)=\(\left(\begin{array}{l}
2 \\
3
\end{array}\right)\)
Converting the matrix equation to a system of linear equations gives us
x + ky =2
ky =3.
Solve this system.
y = \(\frac{3}{k}\)
x + k(\(\frac{3}{k}\))=2
x + 3 =2
x =-1
The point is \(\left(\begin{array}{l}
x \\
y
\end{array}\right)\)= \(\left(\begin{array}{c}
-1 \\
\frac{3}{k}
\end{array}\right)\).

d. The transformation \(\left(\begin{array}{ll}
1 & k \\
0 & k
\end{array}\right)\) is applied once to the point \(\left(\begin{array}{l}
1 \\
1
\end{array}\right)\), then once to the image point, then once to the image of the image point, and then once to the image of the image of the image point, and so on. What are the coordinates of a tenfold image of the point \(\left(\begin{array}{l}
1 \\
1
\end{array}\right)\), that is, the image of the point after the transformation has been applied 10 times?
Answer:
Multiply to apply the transformation once: \(\left(\begin{array}{ll}
1 & k \\
0 & k
\end{array}\right)\left(\begin{array}{l}
1 \\
1
\end{array}\right)\) = \(\left(\begin{array}{c}
1+k \\
k
\end{array}\right)\)
Multiply again by the 2×2 matrix: \(\left(\begin{array}{ll}
1 & k \\
0 & k
\end{array}\right)\left(\begin{array}{c}
1+k \\
k
\end{array}\right)\)=\(\left(\begin{array}{c}
1+k+k^{2} \\
k^{2}
\end{array}\right)\)
Multiply again by the 2×2 matrix: \(\left(\begin{array}{cc}
1 & k \\
0 & k
\end{array}\right)\left(\begin{array}{c}
1+k+k^{2} \\
k^{2}
\end{array}\right)\)=\(\left(\begin{array}{c}
1+k+k^{2}+k^{3} \\
k^{3}
\end{array}\right)\).
By observing the patterns, we can see that the result of n multiplications is a
2×1 matrix whose top row is the previous row plus kⁿ and whose bottom row is kⁿ. The tenfold image would be \(\left(\begin{array}{c}
1+k+k^{2}+k^{3}+\ldots k^{10} \\
k^{10}
\end{array}\right)\).

Question 2.
Consider the transformation given by \(\left(\begin{array}{cc}
\cos (1) & -\sin (1) \\
\sin (1) & \cos (1)
\end{array}\right)\).

a. Describe the geometric effect of applying this transformation to a point \(\left(\begin{array}{l}
x \\
y
\end{array}\right)\) in the plane.
Answer:
This transformation will rotate the point \(\left(\begin{array}{l}
x \\
y
\end{array}\right)\) counterclockwise about the origin through an angle of 1 radian.

b. Describe the geometric effect of applying this transformation to a point \(\left(\begin{array}{l}
x \\
y
\end{array}\right)\) in the plane twice: once to the point and then once to its image.
Answer:
This transformation will rotate the point \(\left(\begin{array}{l}
x \\
y
\end{array}\right)\) counterclockwise about the origin an additional 1 radian for a total rotation of 2 radians.

c. Use part (b) to prove cos⁡ (2)=cos² (1)-sin² (1) and sin⁡(2)=2 sin⁡(1)cos(1).
Answer:
To prove this, multiply \(\left(\begin{array}{l}
x \\
y
\end{array}\right)\) by the transformation matrix:

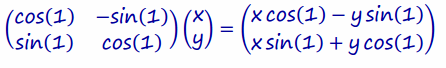
Then, multiply this answer by the transformation matrix:

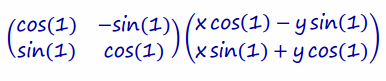
Apply matrix multiplication:

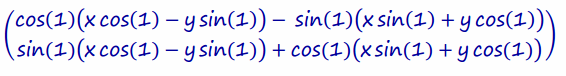
Distribute:

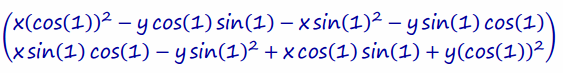
Rearrange and factor:

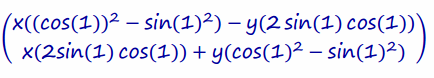
This matrix is equal to the matrix resulting from the 2-radian rotation.

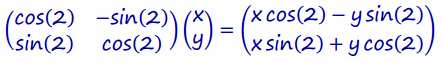
When you equate the answers and compare the coefficients of x and y, you can see that
cos⁡(2)=cos⁡(1)²-sin⁡(1)² and sin⁡(2)=2 sin⁡(1) cos⁡(1) .
The matrices are equal because they represent the same transformation.

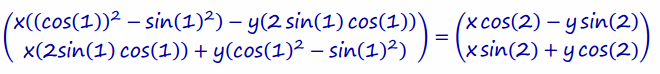
Question 3.
Explain the geometric representation of multiplying by 1+i.
Answer:
1 + i has argument \(\frac{\pi}{4}\) and modulus \(\sqrt{2}\), so geometrically this represents a dilation with a scale factor of \(\sqrt{2}\) and a counterclockwise rotation of \(\frac{\pi}{4}\) about the origin.

b. Write (1+i)¹⁰ as a complex number of the form a+bi for real numbers a and b.
Answer:
1 + i has argument \(\frac{\pi}{4}\) and modulus \(\sqrt{2}\), and so (1 + i)¹⁰ has argument 10 × \(\frac{\pi}{4}\) = \(\frac{\pi}{2}\) + 2π and modulus (\(\sqrt{2}\))¹⁰ =2⁵ = 32. Thus, (1 + i)¹⁰ = 32i.

c. Find a complex number a+bi, with a and b positive real numbers, such that (a+bi)³=i.
Answer:
i has argument \(\frac{\pi}{2}\) and modulus 1. Thus, a complex number a + bi of argument \(\frac{\pi}{6}\) and modulus 1 will satisfy (a + bi)³ = i. We have a + bi = \(\frac{\sqrt{3}}{2}\) + i\(\frac{1}{2}\).

d. If z is a complex number, is there sure to exist, for any positive integer n, a complex number w such that wⁿ=z? Explain your answer.
Answer:
Yes. If z = 0, then w = 0 works. If, on the other hand, z is not zero and has argument θ and modulus m, then let w be the complex number with argument \(\frac{θ}{n}\) and modulus \(m^{\frac{1}{n}}\):
w =\(m^{\frac{1}{n}}\) (cos⁡(\(\frac{θ}{n}\))+ i sin⁡(\(\frac{θ}{n}\))).

e. If z is a complex number, is there sure to exist, for any negative integer n, a complex number w such that wⁿ=z? Explain your answer.
Answer:
If z = 0, then there is no such complex number w. If z ≠ 0, then \(\frac{1}{w}\), with w as given in part (c), satisfies \(\frac{1}{w}\)^-n = z, showing that the answer to the question is yes in this case.

Question 4.
Let P=\(\left(\begin{array}{ll}
0 & 0 \\
1 & 0
\end{array}\right)\) and O=\(\left(\begin{array}{ll}
0 & 0 \\
0 & 0
\end{array}\right)\).

a. Give an example of a 2×2 matrix A, not with all entries equal to zero, such that PA=O.
Answer:
Notice that for any matrix A = \(\left(\begin{array}{ll}
a & b \\
c & d
\end{array}\right)\), we have PA = \(\left(\begin{array}{ll}
0 & 0 \\
1 & 0
\end{array}\right)\left(\begin{array}{ll}
a & b \\
c & d
\end{array}\right)\left(\begin{array}{ll}
0 & 0 \\
a & b
\end{array}\right)\).
If we choose A = \(\left(\begin{array}{ll}
0 & 0 \\
1 & 1
\end{array}\right)\), for example, then PA = O.

b. Give an example of a 2×2 matrix B with PB≠O.
Answer:
Following the discussion in part (a), we see that choosing A = \(\left(\begin{array}{ll}
1 & 1 \\
0 & 0
\end{array}\right)\) gives PA = \(\left(\begin{array}{ll}
0 & 0 \\
1 & 1
\end{array}\right)\), which is different from O.

c. Give an example of a 2×2 matrix C such that CR=R for all 2×2 matrices R.
Answer:
Choose C = \(\left(\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right)\). The identity matrix has this property.

d. If a 2×2 matrix D has the property that D+R=R for all 2×2 matrices R, must D be the zero matrix O? Explain.
Answer:
Write D = \(\left(\begin{array}{ll}
a & b \\
c & d
\end{array}\right)\) and R=\(\left(\begin{array}{cc}
x & y \\
z & w
\end{array}\right)\). Then, for D + R = \(\left(\begin{array}{ll}
a+x & b+y \\
c+z & d+w
\end{array}\right)\) to equal \(\left(\begin{array}{ll}
x & y \\
z & w
\end{array}\right)\) no matter the values of x,y,z, and w, we need:
a + x = x
b + y = y
c + z = z
d + w = w
to hold for all values x, y, z, and w. Thus, we need a = 0, b = 0, c = 0, and d = 0. That is, D must indeed be the zero matrix.

e. Let E=\(\left(\begin{array}{ll}
2 & 4 \\
3 & 6
\end{array}\right)\). Is there a 2×2 matrix F so that EF=\(\left(\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right)\) and FE=\(\left(\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right)\)? If so, find one. If not, explain why no such matrix F can exist.
The determinant of E is |2 ∙ 6 – 3 ∙ 4|= 0, and so no inverse matrix like F can exist.
Alternatively:
Write F =\(\left(\begin{array}{ll}
a & b \\
c & d
\end{array}\right)\). Then, EF =\(\left(\begin{array}{cc}
2 a+4 c & 2 b+4 d \\
3 a+6 c & 3 b+3 d
\end{array}\right)\). For this to equal \(\left(\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right)\), we need, at the very least:
2a + 4c = 1
3a + 6c = 0
The first of these equations gives a + 2c = \(\frac{1}{2}\) and the second a + 2c = 0. There is no solution to this system of equations, and so there can be no matrix F with the desired property.

Question 5.
In programming a computer video game, Mavis coded the changing location of a space rocket as follows:
At a time t seconds between t=0 seconds and t=2 seconds, the location \(\left(\begin{array}{l}
x \\
y
\end{array}\right)\) of the rocket is given by:

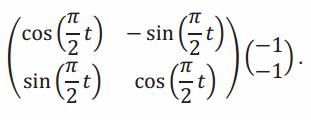
At a time of t seconds between t=2 seconds and t=4 seconds, the location of the rocket is given by \(\left(\begin{array}{l}
3-t \\
3-t
\end{array}\right)\).

a. What is the location of the rocket at time t=0? What is its location at time t=4?
Answer:
At time t = 0, the location of the rocket is

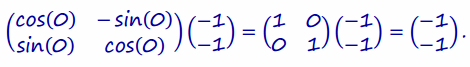
At time t = 4, the location of the rocket is
\(\left(\begin{array}{l}
3-4 \\
3-4
\end{array}\right)\) = \(\left(\begin{array}{l}
-1 \\
-1
\end{array}\right)\),
the same as at the start.

b. Petrich is worried that Mavis may have made a mistake and the location of the rocket is unclear at time t=2 seconds. Explain why there is no inconsistency in the location of the rocket at this time.
Answer:
According to the first set of instructions, the location of the rocket at time t = 2 is

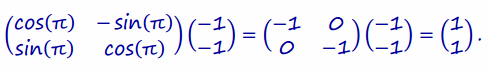
According to the second set of instructions, its location at this time is
\(\left(\begin{array}{l}
3-2 \\
3-2
\end{array}\right)\) = \(\left(\begin{array}{l}
1 \\
1
\end{array}\right)\)
These are consistent.

c. What is the area of the region enclosed by the path of the rocket from time t=0 to time t=4?
Answer:
The path traversed is a semicircle with a radius of \(\sqrt{2}\). The area enclosed is \(\frac{1}{2}\)×2π=π squared units.

d. Mavis later decided that the moving rocket should be shifted five places farther to the right. How should she adjust her formulations above to accomplish this translation?
Answer:
Notice that:

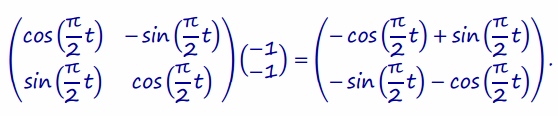
To translate these points 5 units to the right, use
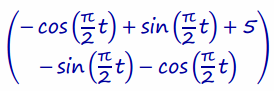for 0≤t≤2.
Also, use