Engage NY Eureka Math Precalculus Module 1 Mid Module Assessment Answer Key
Eureka Math Precalculus Module 1 Mid Module Assessment Task Answer Key
Question 1.
Given z=3-4i and w=-1+5i:
a. Find the distance between z and w.
Answer:
Distance = \(\sqrt{(3-(-1))^{2}-(-1)+((-4)-5)^{2}}\)
=\(\sqrt{4^{2}+(-9)^{2}}\)
= \(\sqrt{16+81}\)
= \(\sqrt{97}\)
b. Find the midpoint of the segment joining z and w.
Answer:
Midpoint =\(\frac{3+(-1)}{2}\) + \(\frac{(-4)+5}{2} i\)
=\(\frac{2}{2}\) +\(\frac{1}{2} i\)
=1+\(\frac{1}{2}\)i
Question 2.
Let z1=2-2i and z2=(1-i)+\(\sqrt{3}\)(1+i).
a. What is the modulus and argument of z1?
Answer:
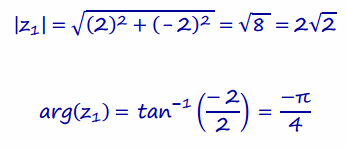
b. Write z1 in polar form. Explain why the polar and rectangular forms of a given complex number represent the same number.
z1 = 2\(\sqrt{2}\) [cos((-\(\frac{\pi}{4}\))+i sin((-\(\frac{\pi}{4}\))]
The modulus represents the distance from the origin to the point. The degree of rotation is the angle from the x-axis. When the polar form is expanded, the result is the rectangular form of a complex number.
c. Find a complex number w, written in the form w=a+ib, such that wz1=z2.
Answer:
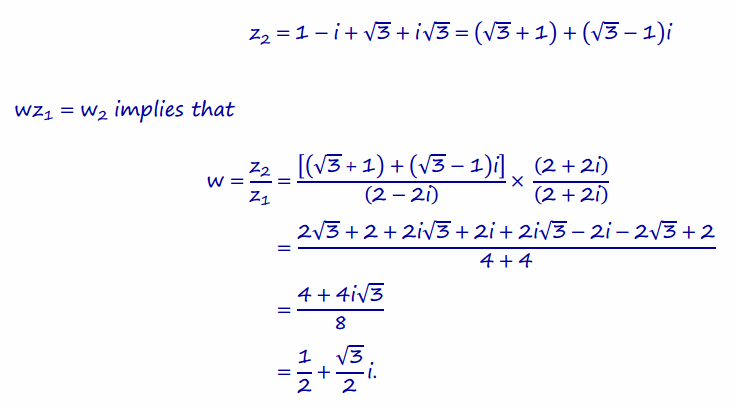
d. What is the modulus and argument of w?
Answer:
|w| = \(\sqrt{\left(\frac{1}{2}\right)^{2}+\left(\frac{\sqrt{3}}{2}\right)^{2}}\) = \(\sqrt{\frac{1}{4}+\frac{3}{4}}\) = 1
arg (w )=tan-1(\(\frac{\frac{\sqrt{3}}{2}}{\frac{1}{2}}\))=\(\frac{\pi}{3}\)
e. Write w in polar form.
Answer:
w=1 [cos(\(\frac{\pi}{3}\))+i sin (\(\frac{\pi}{3}\)) ]
f. When the points z1 and z2 are plotted in the complex plane, explain why the angle between z1 and z2 measures arg(w).
Answer:
Since z2 = wz1, then z2is the transformation of z1 rotated counterclockwise by arg (w ), which is \(\frac{\pi}{3}\).
g. What type of triangle is formed by the origin and the two points represented by the complex numbers z1 and z2? Explain how you know.
Answer:
Since |w | = 1 and arg (w ) = \(\frac{\pi}{3}\), the triangle formed by the origin and the points representing z1 and z2will be equilateral. All of the angles are 60° in this triangle.
h. Find the complex number, v, closest to the origin that lies on the line segment connecting z1 and z2. Write v in rectangular form.
Answer:
The point that represents v is the midpoint of the segment connecting z1 and z2since it must be on the perpendicular bisector of the triangle with vertex at the origin.
To find the midpoint, average z1 and z2.
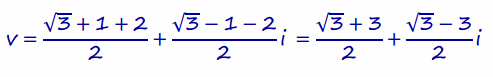
Question 3.
Let z be the complex number 2+3i lying in the complex plane.
a. What is the conjugate of z? Explain how it is related geometrically to z.
Answer:
\(\overline{\boldsymbol{Z}}\)= 2-3i
This number is the conjugate of z and the reflection of z across the horizontal axis.
b. Write down the complex number that is the reflection of z across the vertical axis. Explain how you determined your answer.
Answer:
This number is -2 + 3i . The real coordinate has the opposite sign, but the imaginary part keeps the same sign. This means a reflection across the imaginary (vertical) axis.
Let m be the line through the origin of slope \(\frac{1}{2}\) in the complex plane.
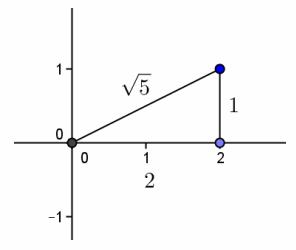
c. Write down a complex number, w, of modulus 1 that lies on m in the first quadrant in rectangular form.
Answer:
Because the slope of m is \(\frac{1}{2}\), the argument of w is tan-1(\(\frac{1}{2}\)).
Using the polar form of w ,
w = 1 [cos(tan-1(\(\frac{1}{2}\)) ) + isin (tan-1(\(\frac{1}{2}\)) )]. From the triangle shown below, w = \(\frac{2}{\sqrt{5}}\) + \(\frac{1}{\sqrt{5}}\)i .
d. What is the modulus of wz?
Answer:
The modulus of wz is \(\sqrt{13}\).
e. Explain the relationship between wz and z. First, use the properties of modulus to answer this question, and then give an explanation involving transformations.
Answer:
The modulus of wz is \(\sqrt{13}\) and is the same as |z |.
Using the properties of modulus,
|wz | = |w | × |z | = 1 × |z | = 1 × \(\sqrt{2^{2}+3^{2}}\) = \(\sqrt{13}\).
Geometrically, multiplying by w will rotate z by the arg (w ) and dilate z by |w |. Since |w | = 1 , the transformation is a rotation only, so both w and z are the same distance from the origin.
f. When asked,
“What is the argument of \(\frac{1}{w}\)z?”
Paul gave the answer arctan(\(\frac{3}{2}\))-arctan(\(\frac{1}{2}\)), which he then computed to two decimal places. Provide a geometric explanation that yields Paul’s answer.
Answer:
The product \(\frac{1}{w}\)z would result in a clockwise rotation of z by the arg (w ). There would be no dilation since |w | = 1 .
arg (z ) = tan-1(\(\frac{3}{2}\))
arg (w ) = tan-1(\(\frac{1}{2}\))
arg (\(\frac{1}{w}\)z ) = tan-1(\(\frac{3}{2}\)) – tan-1(\(\frac{1}{2}\))
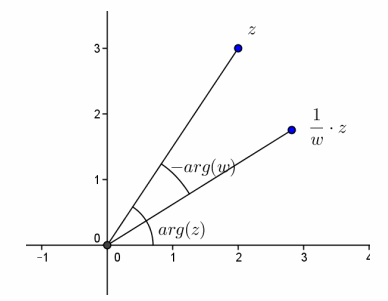
g. When asked,
“What is the argument of \(\frac{1}{w}\)z?”
Mable did the complex number arithmetic and computed z÷w. She then gave an answer in the form arctan(\(\frac{a}{b}\)) for some fraction \(\frac{a}{b}\). What fraction did Mable find? Up to two decimal places, is Mable’s final answer the same as Paul’s?
Answer:
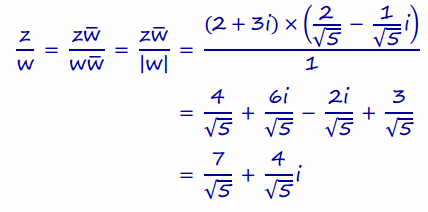
Comparing these angles shows they are the same.
tan-1(\(\frac{4}{7}\))≈0.52
tan-1(\(\frac{3}{2}\))- tan-1(\(\frac{1}{2}\))≈0.52