Engage NY Eureka Math 8th Grade Module 7 Lesson 23 Answer Key
Eureka Math Grade 8 Module 7 Lesson 23 Exercise Answer Key
Mathematical Modeling Exercise
A ladder of length L ft. leaning against a wall is sliding down. The ladder starts off being flush with (right up against) the wall. The top of the ladder slides down the vertical wall at a constant speed of v ft. per second. Let the ladder in the position L1 slide down to position L2 after 1 second, as shown below.
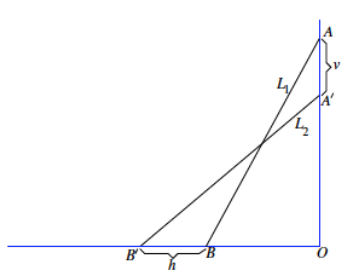
Will the bottom of the ladder move at a constant rate away from point O?
Answer:
→ Identify what each of the symbols in the diagram represents.
O represents the corner where the floor and the wall intersect.
L1 represents the position of the ladder after it has slid down the wall.
L2 represents the position of the ladder after it has slid one second after position L1 down the wall.
A represents the starting position of the top of the ladder.
A’ represents the position of the top of the ladder after it has slid down the wall for one second.
v represents the distance that the ladder slid down the wall in one second.
B represents the starting position of the bottom of the ladder.
B’ represents the position of the bottom of the ladder after it has slid for one second.
h represents the distance the ladder has moved along the ground after sliding down the wall in one second.
→ The distance from point A to point A’ is v ft. Explain why.
Since the ladder is sliding down the wall at a constant rate of v ft. per second, then after 1 second, the ladder moves v feet. Since we are given that the time it took for the ladder to go from position L1 to L2 is one second, then we know the distance between those points must be v feet.
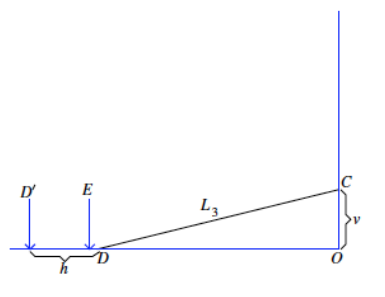
→ The bottom of the ladder then slides on the floor to the left so that in 1 second it moves from B to B’ as shown. Therefore, the average speed of the bottom of the ladder is h ft. per second in this 1-second interval. Will the bottom of the ladder move at a constant rate away from point O? In other words, if the ladder moves at a constant rate, will the distance it has moved (shown as D’ in the image below) coincide with point E where |EO| is the length of the ladder?
Answer:
Provide time for students to discuss the answer to the question in pairs or small groups, and then have students share their reasoning. This question is the essential question of the lesson. The answer to this question is the purpose of the entire investigation.
Consider prompting their thinking with the following questions:
→ Think about the distance the base of the ladder is away from the wall as a function of time t. What do you think the beginning placement of the ladder should be for time t = 0?
→ Flush vertical against the wall
→ How far away from the wall is the base of the ladder then at time t = 0?
→ It is right up against the wall.
→ If we let d represent the distance of the base of the ladder from the wall, we know that at t = 0, d = 0.
→ Can the ladder continue sliding forever? Is there a time at which it must stop sliding?
Yes, it must stop sliding when it lies flat on the floor.
Can we compute at what time that will occur?
Allow students time to struggle with this. They may or may not be able to develop the equation below.
t = \(\frac{L}{v}\)
→ So our question is, is d a linear function of time? That is, does the value of d change by constant amounts over constant time intervals?
Students may suggest modeling the experiment using a note card against a vertical book and observing how the distance changes as the card slides down the book. Students may compare extreme cases where the base of the ladder moves a greater distance in the first second of sliding down the wall as opposed to the last second.
Students should recognize that this situation cannot be described by a linear function. Specifically, if the top of the ladder was v feet from the floor as shown below, it would reach O in one second (because the ladder slides down the wall at a constant rate of v per second). Then after 1 second, the ladder will be flat on the floor, and the foot of the ladder would be at the point where |EO| = L, or the length of the ladder. The discussion points below may be useful if students were unable to determine that the motion is non-linear.
→ If the rate of change could be described by a linear function, then the point D would move to D’ after 1 second, where |D’ D| = h ft . (where h is defined as the length the ladder moved from D to D’ in one second). But this is impossible.
→ Recall that the length of the ladder, L, is |EO|. When the ladder is flat on the floor, then at most, the foot of the ladder will be at point E from point O. If the rate of change of the ladder were linear, then the foot of the ladder would be at D’ because the linear rate of change would move the ladder a distance of h feet every 1 second. From the picture (on the previous page) you can see that D’≠E. Therefore, it is impossible that the rate of change of the ladder could be described by a linear function.
→ Intuitively, if you think about when the top of the ladder, C, is close to the floor (point O), a change in the height of C would produce very little change in the horizontal position of the bottom of the ladder, D.
→ Consider the three right triangles shown below. If we let the length of the ladder be 8 ft., then we can see that a constant change of 1 ft. in the vertical distance produces very little change in the horizontal distance. Specifically, the change from 3 ft. to 2 ft. produces a horizontal change of approximately 0.3 ft., and the change from 2 ft. to 1 ft. produces a horizontal change of approximately 0.2 ft. A change from 1 ft. to 0 ft., meaning that the ladder is flat on the floor, would produce a horizontal change of just 0.1 ft. (the difference between the length of the ladder, 8 ft. and 7.9 ft.)
Consider the three right triangles shown below, specifically the change in the length of the base as the height decreases in increments of 1 ft.

Answer:
→ In particular, when the ladder is flat on the floor so that C = O, then the bottom cannot be further left than the point E because |EO| = L, the length of the ladder. Therefore, the ladder will never reach point D’, and the function that describes the movement of the ladder cannot be linear.
→ We want to show that our intuitive sense of the movement of the ladder is accurate. Our goal is to derive a formula, d, for the function of the distance of the bottom of the ladder from O over time t. Because the top of the ladder slides down the wall at a constant rate of v ft . per second, the top of the ladder is now at point A, which is vt ft. below the vertical height of L feet, and the bottom of the ladder is at point B, as shown below. We want to determine |BO|, which by definition is the formula for the function, d.
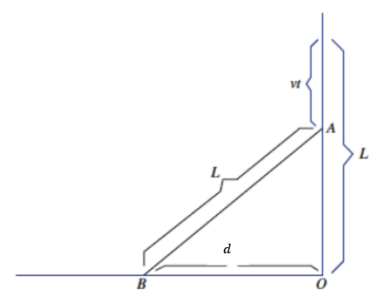
Answer:
→ Explain the expression vt. What does it represent?
The expression vt represents the distance the ladder has slid down the wall after t seconds. Since v is the rate at which the ladder slides down the wall, then vt is the distance it slides after t seconds.
→ How can we determine |BO|?
The shape formed by the ladder, wall, and floor is a right triangle, so we can use the Pythagorean theorem to find |BO|.
→ What is the length of |AO|?
|AO| is the length of the ladder L minus the distance the ladder slides down the wall after t seconds (i.e., vt). Therefore, |AO| = L – vt.
→ What is the length of the hypotenuse of the right triangle?
The length of the hypotenuse is the length of the ladder, L.
Use the Pythagorean theorem to write an expression that gives |BO| (i.e., d).
Provide students time to work in pairs to write the expression for |BO|. Give guidance as necessary.
By the Pythagorean theorem,
(L-vt)2+d2 = L2
d2 = L2-(L-vt)2
\(\sqrt{d^{2}}\) = \(\sqrt{L^{2}-(L-v t)^{2}}\)
d = \(\sqrt{L^{2}-(L-v t)^{2}}\)
Pause after deriving the equation d = \(\sqrt{L^{2}-(L-v t)^{2}}\). Ask students to explain what the equation represents. Students should recognize that the equation gives the distance the foot of the ladder is from the wall, which is |BO|.
→ Let’s return to an earlier question: Will the ladder continue to slide forever?
The goal is for students to conclude that when d = L, the ladder will no longer slide. That is, when
\(\sqrt{L^{2}-(L-v t)^{2}}\) = L, the ladder is finished sliding. If students need convincing, consider the following situation with concrete numbers.
What would happen if t were very large? Suppose the constant rate, v, of the ladder falling down the wall is
2 feet per second, the length of the ladder, L, is 10 feet, and the time t is 100 seconds—what is d equal to?
The value of d is
d = \(\sqrt{L^{2}-(L-v t)^{2}}\)
= \(\sqrt{10^{2}-(10-2(100))^{2}}\)
= \(\sqrt{100-(190)^{2}}\)
= \(\sqrt{100-36,100}\)
= \(\sqrt{-36,000}\)
If the value of t were very large, then the formula would make no sense because the length of |BO| would be equal to the square of a negative number.
For this reason, we can only consider values of t so that the top of the ladder is still above the floor. Symbolically, vt≤L, where vt is the expression that describes the distance the ladder has moved at a specific rate v for a specific time t. We need that distance to be less than or equal to the length of the ladder.
→ What happens when t = \(\frac{L}{v}\)? Substitute \(\frac{L}{v}\) for t in our formula.
Substituting \(\frac{L}{v}\) for t,
d = \(\sqrt{L^{2}-(L-v t)^{2}}\)
= \(\sqrt{L^{2}-\left(L-v\left(\frac{L}{v}\right)\right)^{2}}\)
= \(\sqrt{L^{2}-(L-L)^{2}}\)
= \(\sqrt{L^{2}-0^{2}}\)
= \(\sqrt{L^{2}}\)
= L.
When t = \(\frac{L}{v}\), the top of the ladder will be at the point O, and the ladder will be flat on the floor because d represents the length of |BO|. If that length is equal to L, then the ladder must be on the floor.
→ Back to our original concern: What kind of function describes the rate of change of the movement of the bottom of the ladder on the floor? It should be clear that by the equation d = \(\sqrt{L^{2}-(L-v t)^{2}}\), which represents |BO| for any time t, that the motion (rate of change) is not one of constant speed. Nevertheless, thanks to the concept of a function, we can make predictions about the location of the ladder for any value of t as long as t≤\([latex]\frac{L}{v}\)[/latex]
→ We will use some concrete numbers to compute the average rate of change over different time intervals. Suppose the ladder is 15 feet long, L = 15, and the top of the ladder is sliding down the wall at a constant speed of 1 ft. per second, v = 1. Then, the horizontal distance of the bottom of the ladder from the wall (|BO|) is given by the formula
d = \(\sqrt{15^{2}-(15-1 t)^{2}}\)
= \(\sqrt{225-(15-t)^{2}}\)
Determine the outputs the function would give for the specific inputs. Use a calculator to approximate the lengths. Round to the hundredths place.

Answer:
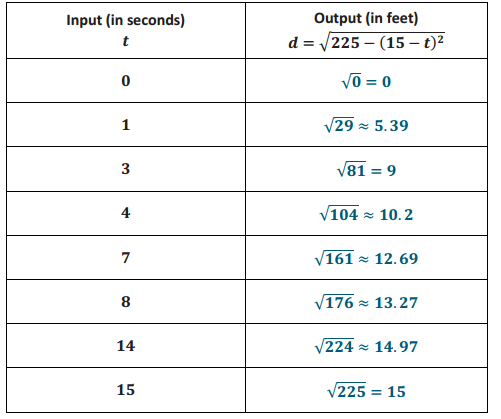
Make at least three observations about what you notice from the data in the table. Justify your observations mathematically with evidence from the table.
→ Sample observations given below.
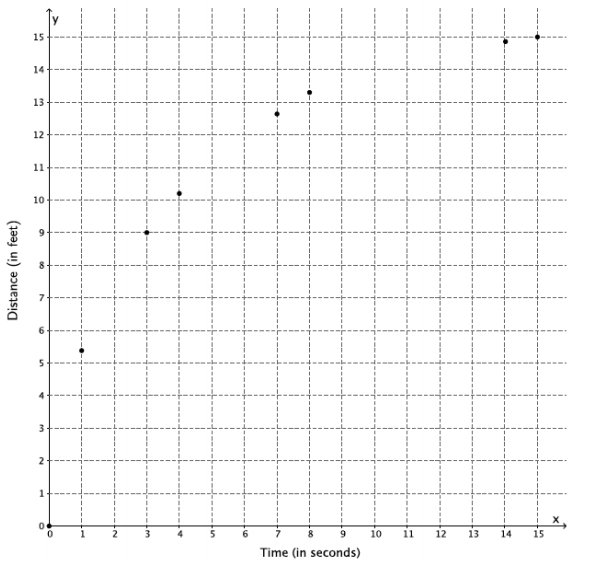
The average rate of change between 0 and 1 second is 5.39 feet per second.
\(\frac{5.39-0}{1-0}\) = 5.39
The average rate of change between 3 and 4 seconds is 1.2 feet per second.
\(\frac{10.2-9}{4-3}\) = 1.2
The average rate of change between 7 and 8 seconds is 0.58 feet per second.
\(\frac{13.27-12.69}{8-7}\) = 0.58
The average rate of change between 14 and 15 seconds is 0.03 feet per second.
\(\frac{15-14.97}{15-14}\) = 0.03
→ Now that we have computed the average rate of change over different time intervals, we can make two conclusions: (1) The motion at the bottom of the ladder is not linear, and (2) there is a decrease in the average speeds; that is, the rate of change of the position of the ladder is slowing down as observed in the four 1-second intervals we computed. These conclusions are also supported by the graph of the situation shown on the next page. The data points do not form a line; therefore, the rate of change with respect to the position of the bottom of the ladder is not linear.
Eureka Math Grade 8 Module 7 Lesson 23 Problem Set Answer Key
Question 1.
Suppose the ladder is 10 feet long, and the top of the ladder is sliding down the wall at a rate of 0.8 ft. per second. Compute the average rate of change in the position of the bottom of the ladder over the intervals of time from 0 to 0.5 seconds, 3 to 3.5 seconds, 7 to 7.5 seconds, 9.5 to 10 seconds, and 12 to 12.5 seconds. How do you interpret these numbers?

Answer:
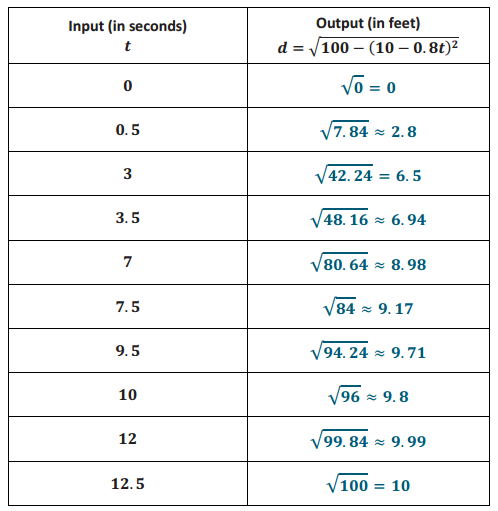
The average rate of change between 0 and 0.5 seconds is 5.6 feet per second.
\(\frac{2.8-0}{0.5-0}\) = \(\frac{2.8}{0.5}\) = 5.6
The average rate of change between 3 and 3.5 seconds is 0.88 feet per second.
\(\frac{6.94-6.5}{3.5-3}\) = \(\frac{0.44}{0.5}\) = 0.88
The average rate of change between 7 and 7.5 seconds is 0.38 feet per second.
\(\frac{9.17-8.98}{7.5-5}\) = \(\frac{0.19}{0.5}\) = 0.38
The average rate of change between 9.5 and 10 seconds is 0.18 feet per second.
\(\frac{9.8-9.71}{10-9.5}\) = \(\frac{0.09}{0.5}\) = 0.18
The average rate of change between 12 and 12.5 seconds is 0.02 feet per second.
\(\frac{10-9.99}{12.5-12}\) = \(\frac{0.01}{0.5}\) = 0.02
The average speeds show that the rate of change in the position of the bottom of the ladder is not linear. Furthermore, it shows that the rate of change in the position at the bottom of the ladder is quick at first, 5.6 feet per second in the first half second of motion, and then slows down to 0.02 feet per second in the half-second interval from 12 to 12.5 seconds.
Question 2.
Will any length of ladder, L, and any constant speed of sliding of the top of the ladder, v ft. per second, ever produce a constant rate of change in the position of the bottom of the ladder? Explain.
Answer:
No, the rate of change in the position at the bottom of the ladder will never be constant. We showed that if the rate were constant, there would be movement in the last second of the ladder sliding down that wall that would place the ladder in an impossible location. That is, if the rate of change were constant, then the bottom of the ladder would be in a location that exceeds the length of the ladder. Also, we determined that the distance that the bottom of the ladder is from the wall over any time period can be found using the formula d = \(\sqrt{L^{2}-(L-v t)^{2}}\), which is a non-linear equation. Since graphs of functions are equal to the graph of a certain equation, the graph of the function represented by the formula d = \(\sqrt{L^{2}-(L-v t)^{2}}\) is not a line, and the rate of change in position at the bottom of the ladder is not constant.
Eureka Math Grade 8 Module 7 Lesson 23 Exit Ticket Answer Key
Question 1.
Suppose a book is 5.5 inches long and leaning on a shelf. The top of the book is sliding down the shelf at a rate of 0.5 in. per second. Complete the table below. Then, compute the average rate of change in the position of the bottom of the book over the intervals of time from 0 to 1 second and 10 to 11 seconds. How do you interpret these numbers?

Answer:
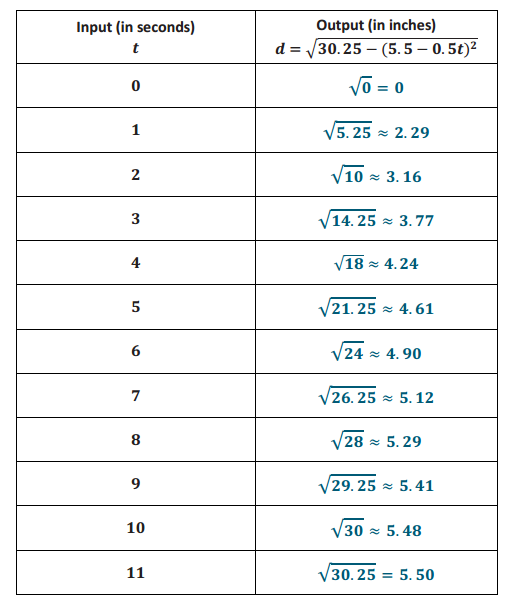
The average rate of change between 0 and 1 second is 2.29 inches per second.
\(\frac{2.29-0}{1-0}\) = \(\frac{2.29}{1}\) = 2.29.
The average rate of change between 10 and 11 seconds is 0.02 inches per second.
\(\frac{5.5-5.48}{11-10}\) = \(\frac{0.02}{1}\) = 0.02.
The average speeds show that the rate of change of the position of the bottom of the book is not linear. Furthermore, it shows that the rate of change of the bottom of the book is quick at first, 2.29 inches per second in the first second of motion, and then slows down to 0.02 inches per second in the one second interval from 10 to 11 seconds.