Engage NY Eureka Math 8th Grade Module 7 End of Module Assessment Answer Key
Eureka Math Grade 8 Module 7 End of Module Assessment Task Answer Key
When using a calculator to complete the assessment, use the π key and the full display of the calculator for computations.
Question 1.
a. Is a triangle with side lengths of 7 cm, 24 cm, and 25 cm a right triangle? Explain.
Answer:
72 + 242 = 252
49 + 576 = 625
625 = 625
Yes. The lengths 7,24,25 satisfy the Pythagorean theorem, therefore, it is a right triangle.
b. Is a triangle with side lengths of 4 mm, 11 mm, and 15 mm a right triangle? Explain.
Answer:
42 + 112 = 152
16 + 121 = 225
137 ≠ 225
No. The lengths 4, 11, 15 do not satisfy the Pythagorean theorem, therefore, it is not a right triangle.
c. The area of the right triangle shown below is 30 ft2. The segment XY has a length of 5 ft. Find the length of the hypotenuse.
Answer:
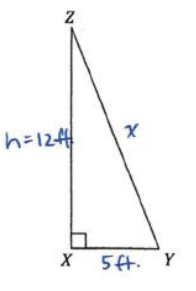
\(\frac{1}{2}\) = 30
5h = 60
h = 12
52 + 122 = x2
25 + 144 = x2
169 = x2
\(\sqrt{169}\) = x
13 = x
The length of the hypotenuse is 13ft.
d. Two paths from school to the store are shown below: One uses Riverside Drive, and another uses Cypress and Central Avenues. Which path is shorter? By about how much? Explain how you know.
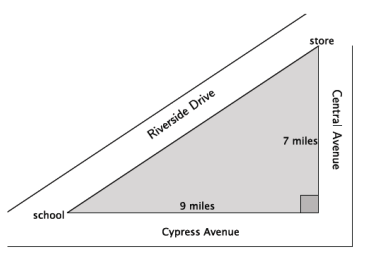
Answer:
Let c be the hypotenuse in miles.
72 + 92 = c2
49 + 81 = c2
130 = c2
\(\sqrt{130}\) = \(\sqrt{c^{2}}\)
\(\sqrt{130}\) = c
11.4 ≈ c
The path along Riverside Drive is shorter, about 11.4miles, compared to the path along Cypress and Control Avenues, 16 miles. The difference is about 4.6 miles. The Pythagorean theorem allowed me to calculate the distance along Riverside Drive because the three roads from a right triangle.
e. What is the distance between points A and B?
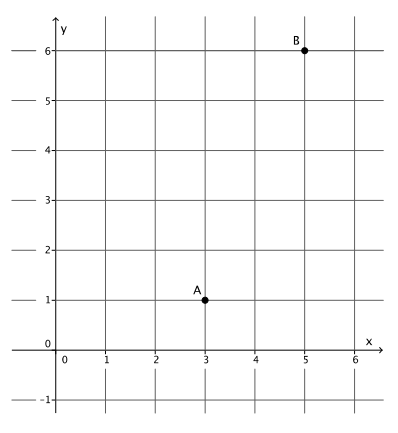
Answer:
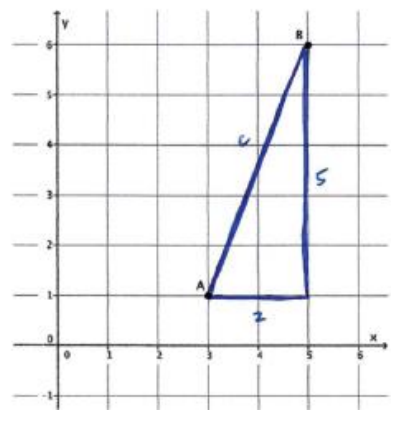
Let c be the distance between points A & B.
22 + 52 = c2
4 + 25 = c2
\(\sqrt{29}\) = \(\sqrt{c^{2}}\)
\(\sqrt{29}\) = c
5.4 ≈ c
The distance between points A & B is about 5.4 units.
f. Do the segments connecting the coordinates (-1, 6), (4, 2), and (7, 6) form a right triangle? Show work that leads to your answer.
Answer:
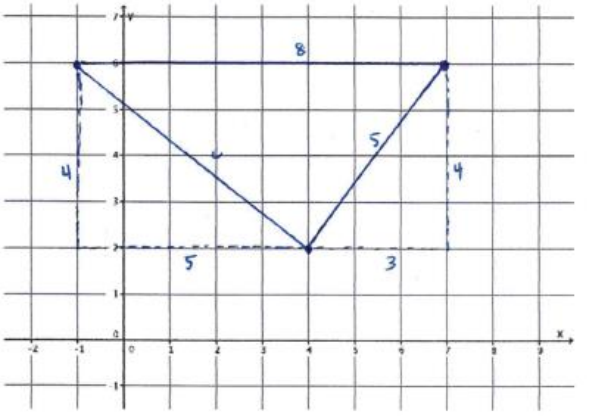
32 + 42 = 52
9 + 16 = 25
25 = 25
42 + 52 = c2
16 + 25 = c2
\(\sqrt{41}\) = \(\sqrt{c^{2}}\)
\(\sqrt{41}\) = c
6 < \(\sqrt{41}\) < 7, So side 8 units is the longest.
52 + (\(\sqrt{41}\))2 = 8 2
25 + 41 = 64
66 ≠ 64
No. The segment connecting (-1, 6), (4, 2), and (7, 6) do not form a right triangle because their lengths do not satisfy the Pythagorean theorem.
g. Using an example, illustrate and explain the Pythagorean theorem.
Answer:
Given a right triangle ABC, the sides a, b, c (Where c is the hypotenuse) satisfy a2 + b2 = c2
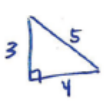
a = 3, b = 4, c = 5
32 + 42 = 52
9 + 16 = 25
25 = 25
h. Using a different example than in part (g), illustrate and explain the converse of the Pythagorean theorem.
Answer:
Given a triangle ABC with side lengths a, b, c (where c is the hypotenuse) that satisfies a2 + b2 = c2, then triangle ABC is a right triangle.
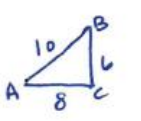
62 + 82 = 102
36 + 64 = 100
100 = 100
Therefore, triangle ABC is a right triangle because it satisfies the converse of the Pythagorean theorem.
i. Explain a proof of the Pythagorean theorem and its converse.
Answer:
See rubric to locate proofs of the theorem and its converse within the module.
Question 2.
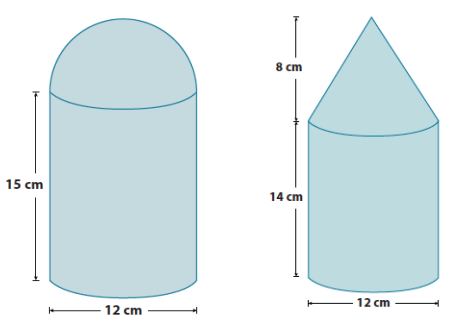
Dorothy wants to purchase a container that will hold the most sugar. Assuming each of the containers below can be completely filled with sugar, write a note recommending a container, including justification for your choice.
Note: The figures are not drawn to scale.
Answer:
Cylinder:
V = 62 π (15)
= 540π
\(\frac{1}{2}\) Sphere:
V = \(\frac{1}{2}\) (\(\frac{4}{3}\)) π 63
= \(\frac{2}{3}\) (216) π
= 144π
Total Volume:
540π + 144π = 684π
Cylinder:
V = 62 π (14)
= 504π
Cone:
V = \(\frac{1}{3}\)π (62) 8
= 96π
Total Volume:
504π + 96π = 600π
Dorothy,
You should choose the container with the half sphere on top because it has a greater volume than the container with the cone on top. The containers have volumes of 684π cm3 and 600π cm3, respectively. Since 684 π is greater than 600π, then the container with the half sphere will held more sugar compared to the container with the cone on top.
Question 3.
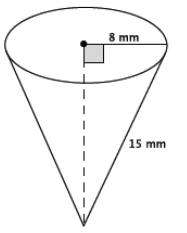
a. Determine the volume of the cone shown below. Give an answer in terms of π and an approximate answer rounded to the tenths place.
Answer:
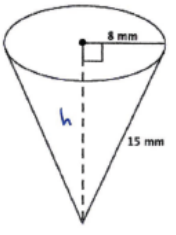
82 + h2 = 152
64 + h2 = 225
h2 = 161
\(\sqrt{h^{2}}\) = \(\sqrt{161}\)
h = \(\sqrt{161}\)
V = \(\frac{1}{3}\) π(64) (\(\sqrt{161}\))
= \(\frac{64}{3}\) \(\sqrt{161}\) π
≈ 850.4
The volume of the cone is exactly \(\frac{64}{3}\) \(\sqrt{161}\) π mm3 and approximately 850.4 mm3
b. The distance between the two points on the surface of the sphere shown below is 10 inches. Determine the volume of the sphere. Give an answer in terms of π and an approximate answer rounded to a whole number.
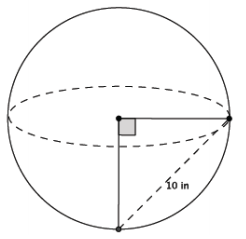
Answer:
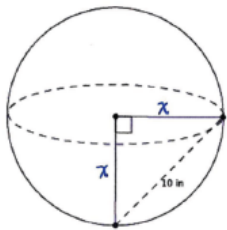
x2 + x2 = 102
2x2 = 100
x2 = 50
\(\sqrt{x^{2}}\) = \(\sqrt{50}\)
x = \(\sqrt{50}\)
V = \(\frac{4}{3}\)π (\(\sqrt{50}\))3
≈ 1481
The volume of the sphere is exactly \(\frac{4}{3}\)π (\(\sqrt{50}\))3 in3 and approximately 1481 in3.
c. A sphere has a volume of 457 \(\frac{1}{3}\) π in3. What is the radius of the sphere?
Answer:
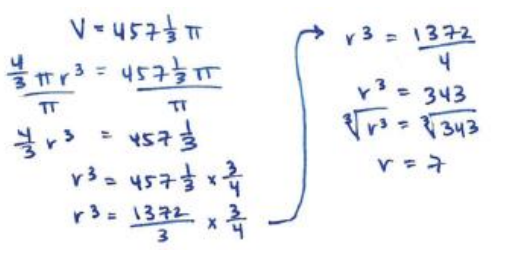
The radius of the sphere is 7 in.