Engage NY Eureka Math 8th Grade Module 5 Lesson 4 Answer Key
Eureka Math Grade 8 Module 5 Lesson 4 Example Answer Key
Example 1.
Classify each of the functions described below as either discrete or not discrete.
a. The function that assigns to each whole number the cost of buying that many cans of beans in a particular grocery store.
b. The function that assigns to each time of day one Wednesday the temperature of Sammy’s fever at that time.
c. The function that assigns to each real number its first digit.
d. The function that assigns to each day in the year 2015 my height at noon that day.
e. The function that assigns to each moment in the year 2015 my height at that moment.
f. The function that assigns to each color the first letter of the name of that color.
g. The function that assigns the number 23 to each and every real number between 20 and 30.6.
h. The function that assigns the word YES to every yes/no question.
i. The function that assigns to each height directly above the North Pole the temperature of the air at that height right at this very moment.
Answer:
a) Discrete
b) Not discrete
c) Not discrete
d) Discrete
e) Not discrete
f) Discrete
g) Not discrete
h) Discrete
i) Not discrete
Example 2.
Water flows from a faucet into a bathtub at a constant rate of 7 gallons of water every 2 minutes Regard the volume of water accumulated in the tub as a function of the number of minutes the faucet has be on. Is this function discrete or not discrete?
Answer:
→ Assuming the tub is initially empty, we determined last lesson that the volume of water in the tub is given by y = 3.5x, where y is the volume of water in gallons, and x is the number of minutes the faucet has been on.
→ What limitations are there on x and y?
Both x and y should be positive numbers because they represent time and volume.
→ Would this function be considered discrete or not discrete? Explain.
This function is not discrete because we can assign any positive number to x, not just positive integers.
Example 3.
You have just been served freshly made soup that is so hot that it cannot be eaten. You measure the temperature of the soup, and it is 210°F. Since 212°F is boiling, there is no way it can safely be eaten yet. One minute after receiving the soup, the temperature has dropped to 203°F. If you assume that the rate at which the soup cools is constant, write an equation that would describe the temperature of the soup over time.
Answer:
The temperature of the soup dropped 7°F in one minute. Assuming the cooling continues at the same rate, then if y is the temperature of the soup after x minutes, then, y = 210 – 7x.
→ We want to know how long it will be before the temperature of the soup is at a more tolerable temperature of 147°F. The difference in temperature from 210°F to 147°F is 63°F. For what number x will our function have the value 147?
147 = 210 – 7x; then 7x = 63, and so x = 9.
→ Curious whether or not you are correct in assuming the cooling rate of the soup is constant, you decide to measure the temperature of the soup each minute after its arrival to you. Here’s the data you obtain:
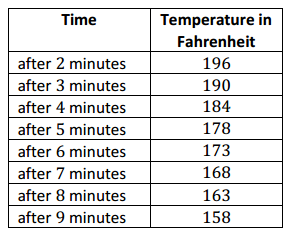
Our function led us to believe that after 9 minutes the soup would be safe to eat. The data in the table shows that it is still too hot.
→ What do you notice about the change in temperature from one minute to the next?
For the first few minutes, minute 2 to minute 5, the temperature decreased 6°F each minute. From minute 5 to minute 9, the temperature decreased just 5°F each minute.
→ Since the rate of cooling at each minute is not constant, this function is said to be a nonlinear function.
→ Sir Isaac Newton not only studied the motion of objects under gravity but also studied the rates of cooling of heated objects. He found that they do not cool at constant rates and that the functions that describe their temperature over time are indeed far from linear. (In fact, Newton’s theory establishes that the temperature of soup at time x minutes would actually be given by the formula y = 70 + 140(\(\frac{133}{140}\))x.)
Example 4.
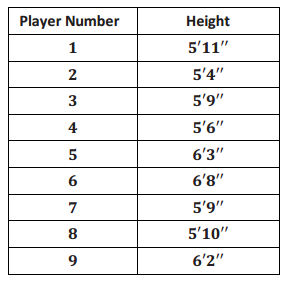
Consider the function that assigns to each of nine baseball players, numbered 1 through 9, his height. The data for this function is given below. Call the function G.
Answer:
→ What output does G assign to the input 2?
The function G assigns the height 5′ 4” to the player 2.
→ Could the function G simultaneously assign a second, different output to player 2? Explain.
No. The function assigns height to a particular player. There is no way that a player can have two different heights.
→ It is not clear if there is a formula for this function. (And even if there were, it is not clear that it would be meaningful since who is labeled player 1, player 2, and so on is probably arbitrary.) In general, we can hope to have formulas for functions, but in reality we cannot expect to find them. (People would love to have a formula that explains and predicts the stock market, for example.)
→ Can we classify this function as discrete or not discrete? Explain.
This function would be described as discrete because the inputs are particular players.
Eureka Math Grade 8 Module 5 Lesson 4 Exercise Answer Key
Exercises 1–3
Exercise 1.
At a certain school, each bus in its fleet of buses can transport 35 students. Let B be the function that assigns to each count of students the number of buses needed to transport that many students on a field trip.
When Jinpyo thought about matters, he drew the following table of values and wrote the formula B = x/35. Here x is the count of students, and B is the number of buses needed to transport that many students. He concluded that B is a linear function.

Alicia looked at Jinpyo’s work and saw no errors with his arithmetic. But she said that the function is not actually linear.
a. Alicia is right. Explain why B is not a linear function.
Answer:
For 36 students, say, we’ll need two buses—an extra bus for the extra student. In fact, for 36,37, …, up to 70 students, the function B assigns the same value 2. For 71,72, …, up to 105, it assigns the value 3. There is not a constant rate of increase of the buses needed, and so the function is not linear.
b. Is B a discrete function?
Answer:
It is a discrete function.
Exercise 2.
A linear function has the table of values below. It gives the costs of purchasing certain numbers of movie tickets.
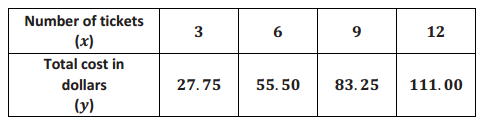
a. Write the linear function that represents the total cost, y, for x tickets purchased.
Answer:
y = \(\frac{27.75}{2}\) x
y = 9.25x
b. Is the function discrete? Explain.
Answer:
The function is discrete. You cannot have half of a movie ticket; therefore, it must be a whole number of tickets, which means it is discrete.
c. What number does the function assign to 4? What do the question and your answer mean?
Answer:
It is asking us to determine the cost of buying 4 tickets. The function assigns 37 to 4. The answer means that 4 tickets will cost $37.00.
Exercise 3.
A function produces the following table of values.
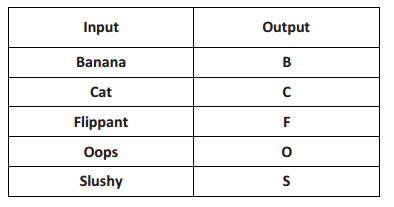
a. Make a guess as to the rule this function follows. Each input is a word from the English language.
Answer:
This function assigns to each word its first letter.
b. Is this function discrete?
Answer:
It is discrete.
Eureka Math Grade 8 Module 5 Lesson 4 Problem Set Answer Key
Question 1.
The costs of purchasing certain volumes of gasoline are shown below. We can assume that there is a linear relationship between x, the number of gallons purchased, and y, the cost of purchasing that many gallons.
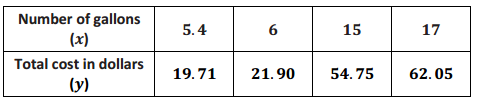
a. Write an equation that describes y as a linear function of x.
Answer:
y = 3.65x
b. Are there any restrictions on the values x and y can adopt?
Answer:
Both x and y must be positive rational numbers.
c. Is the function discrete?
Answer:
The function is not discrete.
d. What number does the linear function assign to 20? Explain what your answer means.
Answer:
y = 3.65(20)
y = 73
The function assigns 73 to 20. It means that if 20 gallons of gas are purchased, it will cost $73.00.
Question 2.
A function has the table of values below. Examine the information in the table to answer the questions below.
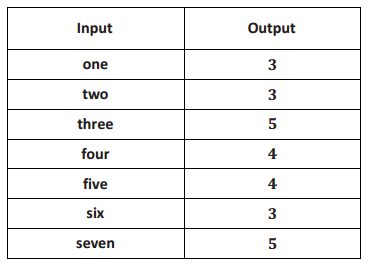
a. Describe the function.
Answer:
The function assigns those particular numbers to those particular seven words. We don’t know if the function accepts any more inputs and what it might assign to those additional inputs. (Though it does seem compelling to say that this function assigns to each positive whole number the count of letters in the name of that whole number.)
b. What number would the function assign to the word eleven?
Answer:
We do not have enough information to tell. We are not even sure if eleven is considered a valid input for this function.
Question 3.
The table shows the distances covered over certain counts of hours traveled by a driver driving a car at a constant speed.

a. Write an equation that describes y, the number of miles covered, as a linear function of x, number of hours driven.
Answer:
y = \(\frac{141}{3}\) x
y = 47x
b. Are there any restrictions on the value x and y can adopt?
Answer:
Both x and y must be positive rational numbers.
c. Is the function discrete?
Answer:
The function is not discrete.
d. What number does the function assign to 8? Explain what your answer means.
Answer:
y = 47(8)
y = 376
The function assigns 376 to 8. The answer means that 376 miles are driven in 8 hours.
e. Use the function to determine how much time it would take to drive 500 miles.
Answer:
500 = 47x
\(\frac{500}{47}\) = x
10.63829… = x
10.6 ≈ x
It would take about 10.6 hours to drive 500 miles.
Question 4.
Consider the function that assigns to each time of a particular day the air temperature at a specific location in Ithaca, NY. The following table shows the values of this function at some specific times.
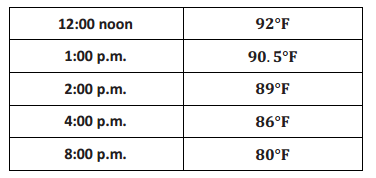
a. Let y represent the air temperature at time x hours past noon. Verify that the data in the table satisfies the linear equation y = 92 – 1.5x.
Answer:
At 12:00, 0 hours have passed since 12:00; then, y = 92 – 1.5(0) = 92.
At 1:00, 1 hour has passed since 12:00; then, y = 92 – 1.5(1) = 90.5.
At 2:00, 2 hours have passed since 12:00; then, y = 92 – 1.5(2) = 89.
At 4:00, 4 hours have passed since 12:00; then, y = 92 – 1.5(4) = 86.
At 8:00, 8 hours have passed since 12:00; then, y = 92 – 1.5(8) = 80.
b. Are there any restrictions on the types of values x and y can adopt?
Answer:
The input is a particular time of the day, and y is the temperature. The input cannot be negative but could be intervals that are fractions of an hour. The output could potentially be negative because it can get that cold.
c. Is the function discrete?
Answer:
The function is not discrete.
d. According to the linear function of part (a), what will the air temperature be at 5:30 p.m.?
Answer:
At 5:30, 5.5 hours have passed since 12:00; then y = 92 – 1.5(5.5) = 83.75.
The temperature at 5:30 will be 83.75°F.
e. Is it reasonable to assume that this linear function could be used to predict the temperature for 10:00 a.m. the following day or a temperature at any time on a day next week? Give specific examples in your explanation.
Answer:
No. There is no reason to expect this function to be linear. Temperature typically fluctuates and will, for certain, rise at some point.
We can show that our model for temperature is definitely wrong by looking at the predicted temperature one week (168 hours) later:
y = 92 – 1.5(168)
y = – 160.
This is an absurd prediction.
Eureka Math Grade 8 Module 5 Lesson 4 Exit Ticket Answer Key
Question 1.
The table below shows the costs of purchasing certain numbers of tablets. We can assume that the total cost is a linear function of the number of tablets purchased.

a. Write an equation that describes the total cost, y, as a linear function of the number, x, of tablets purchased.
Answer:
y = \(\frac{10,183}{17}\) x
y = 599x
b. Is the function discrete? Explain.
Answer:
The function is discrete. You cannot have half of a tablet; therefore, it must be a whole number of tablets, which means it is discrete.
c. What number does the function assign to 7? Explain.
Answer:
The function assigns 4,193 to 7, which means that the cost of 7 tablets would be $4,193.00.
Question 2.
A function C assigns to each word in the English language the number of letters in that word. For example, C assigns the number 6 to the word action.
a. Give an example of an input to which C would assign the value 3.
Answer:
Any three – letter word will do.
b. Is C a discrete function? Explain.
Answer:
The function is discrete. The input is a word in the English language, therefore it must be an entire word, not part of one, which means it is discrete.