Engage NY Eureka Math 8th Grade Module 5 Lesson 3 Answer Key
Eureka Math Grade 8 Module 5 Lesson 3 Example Answer Key
Example 1.
In the last lesson, we looked at several tables of values showing the inputs and outputs of functions. For instance, one table showed the costs of purchasing different numbers of bags of candy:

Answer:
→ What do you think a linear function is?
A linear function is likely a function with a rule described by a linear equation. Specifically, the rate of change in the situation being described is constant, and the graph of the equation is a line.
→ Do you think this is a linear function? Justify your answer.
Yes, this is a linear function because there is a proportional relationship:
\(\frac{10.00}{8}\) = 1.25; $1.25 per each bag of candy
\(\frac{5.00}{4}\) = 1.25; $1.25 per each bag of candy
\(\frac{2.50}{2}\) = 1.25; $1.25 per each bag of candy
The total cost is increasing at a rate of $1.25 with each bag of candy. Further justification comes from the graph of the data shown below.
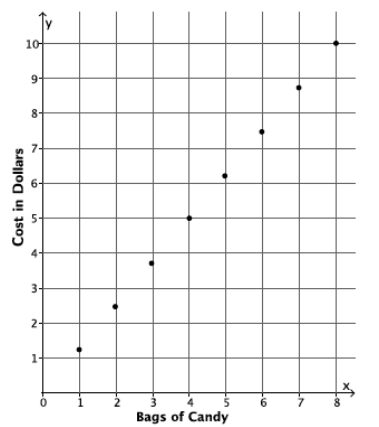
→ A linear function is a function with a rule that can be described by a linear equation. That is, if we use x to denote an input of the function and y its matching output, then the function is linear if the rule for the function can be described by the equation y = mx + b for some numbers m and b.
→ What rule or equation describes our cost function for bags of candy?
The rule that represents the function is then y = 1.25x.
→ Notice that the constant m is 1.25, which is the cost of one bag of candy, and the constant b is 0. Also notice that the constant m was found by calculating the unit rate for a bag of candy.
No matter the value of x chosen, as long as x is a nonnegative integer, the rule y = 1.25x gives the cost of purchasing that many bags of candy. The total cost of candy is a function of the number of bags purchased.
→ Why must we set x as a nonnegative integer for this function?
Since x represents the number of bags of candy, it does not make sense that there would be a negative number of bags. It is also unlikely that we might be allowed to buy fractional bags of candy, and so we require x to be a whole number.
→ Would you say that the table represents all possible inputs and outputs? Explain.
No, it does not represent all possible inputs and outputs. Someone can purchase more than 8 bags of candy, and inputs greater than 8 are not represented by this table (unless the store has a limit on the number of bags one may purchase, perhaps).
Example 2.
Walter walks at a constant speed of 8 miles every 2 hours. Describe a linear function for the number of miles he walks in x hours. What is a reasonable range of x-values for this function?
Answer:
→ Consider the following rate problem: Walter walks at a constant speed of 8 miles every 2 hours. Describe a linear function for the number of miles he walks in x hours. What is a reasonable range of x-values for this function?
Walter’s average speed of walking 8 miles is \(\frac{8}{2}\) = 4, or 4 miles per hour.
→ We have y = 4x, where y is the distance walked in x hours. It seems reasonable to say that x is any real number between 0 and 20, perhaps? (Might there be a cap on the number of hours he walks? Perhaps we are counting up the number of miles he walks over a lifetime?)
→ In the last example, the total cost of candy was a function of the number of bags purchased. Describe the function in this walking example.
The distance that Walter travels is a function of the number of hours he spends walking.
→ What limitations did we put on x?
We must insist that x ≥ 0. Since x represents the time Walter walks, then it makes sense that he would walk for a positive amount of time or no time at all.
→ Since x is positive, then we know that the distance y will also be positive.
Example 3.
Veronica runs at a constant speed. The distance she runs is a function of the time she spends running. The function has the table of values shown below.

Answer:
→ Since Veronica runs at a constant speed, we know that her average speed over any time interval will be the same. Therefore, Veronica’s distance function is a linear function. Write the equation that describes her distance function.
The function that represents Veronica’s distance is described by the equation y = \(\frac{1}{8}\) x, where y is the distance in miles Veronica runs in x minutes and x,y≥0.
→ Describe the function in terms of distance and time.
The distance that Veronica runs is a function of the number of minutes she spends running.
Example 4.
Water flows from a faucet into a bathtub at the constant rate of 7 gallons of water pouring out every 2 minutes. The bathtub is initially empty, and its plug is in. Determine the rule that describes the volume of water in the tub as a function of time. If the tub can hold 50 gallons of water, how long will it take to fill the tub?
Answer:
The rate of water flow is \(\frac{7}{2}\), or 3.5 gallons per minute. Then the rule that describes the volume of water in the tub as a function of time is y = 3.5x, where y is the volume of water, and x is the number of minutes the faucet has been on.
To find the time when y = 50, we need to look at the equation 50 = 3.5x. This gives x = \(\frac{50}{3.5}\) = 14.2857… ≈ 14 . It will take about 14 minutes to fill the tub.
Assume that the faucet is filling a bathtub that can hold 50 gallons of water. How long will it take the faucet to fill the tub?
Since we want the total volume to be 50 gallons, then
50 = 3.5x
\(\frac{50}{3.5}\) = x
14.2857… = x
14 ≈ x
It will take about 14 minutes to fill a tub that has a volume of 50 gallons.
Now assume that you are filling the same 50-gallon bathtub with water flowing in at the constant rate of 3.5 gallons per minute, but there were initially 8 gallons of water in the tub. Will it still take about 14 minutes to fill the tub?
Answer:
No. It will take less time because there is already some water in the tub.

→ What now is the appropriate equation describing the volume of water in the tub as a function of time?
If y is the volume of water that flows from the faucet, and x is the number of minutes the faucet has been on, then y = 3.5x + 8.
→ How long will it take to fill the tub according to this equation?
Since we still want the total volume of the tub to be 50 gallons, then:
50 = 3.5x + 8
42 = 3.5x
12 = x
It will take 12 minutes for the faucet to fill a 50-gallon tub when 8 gallons are already in it.
(Be aware that some students may observe that we can use the previous function rule y = 3.5x to answer this question by noting that we need to add only 42 more gallons to the tub. This will lead directly to the equation 42 = 3.5x.)
→ Generate a table of values for this function:

Example 5.
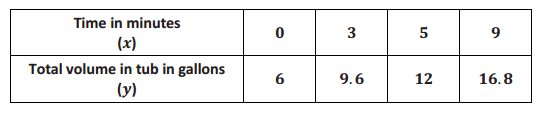
Water flows from a faucet at a constant rate. Assume that 6 gallons of water are already in a tub by the time we notice the faucet is on. This information is recorded in the first column of the table below. The other columns show how many gallons of water are in the tub at different numbers of minutes since we noticed the running faucet.
Answer:
→ After 3 minutes pass, there are 9.6 gallons in the tub. How much water flowed from the faucet in those 3 minutes? Explain.
Since there were already 6 gallons in the tub, after 3 minutes an additional 3.6 gallons filled the tub.
→ Use this information to determine the rate of water flow.
In 3 minutes, 3.6 gallons were added to the tub, then \(\frac{3.6}{3}\) = 1.2, and the faucet fills the tub at a rate of 1.2 gallons per minute.
→ Verify that the rate of water flow is correct using the other values in the table.
Sample student work:
5(1.2) = 6, and since 6 gallons were already in the tub, the total volume in the tub is 12 gallons.
9(1.2) = 10.8, and since 6 gallons were already in the tub, the total volume in the tub is 16.8 gallons.
→ Write an equation that describes the volume of water in the tub as a function of time.
The volume function that represents the rate of water flow from the faucet is y = 1.2x + 6, where y is the volume of water in the tub, and x is the number of minutes that have passed since we first noticed the faucet being on.
→ For how many minutes was the faucet on before we noticed it? Explain.
Since 6 gallons were in the tub by the time we noticed the faucet was on, we need to determine how many minutes it takes for 6 gallons to flow into the tub. The columns for x = 0 and x = 5 in the table show that six gallons of water pour in the tub over a five-minute period. The faucet was on for 5 minutes before we noticed it.
Eureka Math Grade 8 Module 5 Lesson 3 Exercise Answer Key
Exercises 1–3
Exercise 1.
Hana claims she mows lawns at a constant rate. The table below shows the area of lawn she can mow over different time periods.

a. Is the data presented consistent with the claim that the area mowed is a linear function of time?
Answer:
Sample responses:
Linear functions have a constant rate of change. When we compare the rates at each interval of time, they will be equal to the same constant.
When the data is graphed on the coordinate plane, it appears to make a line.
b. Describe in words the function in terms of area mowed and time.
Answer:
The total area mowed is a function of the number of minutes spent mowing.
c. At what rate does Hana mow lawns over a 5-minute period?
Answer:
\(\frac{36}{5}\) = 7.2
The rate is 7.2 square feet per minute.
d. At what rate does Hana mow lawns over a 20-minute period?
Answer:
\(\frac{144}{20}\) = 7.2
The rate is 7.2 square feet per minute.
e. At what rate does Hana mow lawns over a 30-minute period?
Answer:
\(\frac{216}{30}\) = 7.2
The rate is 7.2 square feet per minute.
f. At what rate does Hana mow lawns over a 50-minute period?
Answer:
\(\frac{360}{50}\) = 7.2
The rate is 7.2 square feet per minute.
g. Write the equation that describes the area mowed, y, in square feet, as a linear function of time, x, in minutes.
Answer:
y = 7.2x
h. Describe any limitations on the possible values of x and y.
Answer:
Both x and y must be positive numbers. The symbol x represents time spent mowing, which means it should be positive. Similarly, y represents the area mowed, which should also be positive.
i. What number does the function assign to x = 24? That is, what area of lawn can be mowed in 24 minutes?
Answer:
y = 7.2(24)
y = 172.8
In 24 minutes, an area of 172.8 square feet can be mowed.
j. According to this work, how many minutes would it take to mow an area of 400 square feet?
Answer:
400 = 7.2x
\(\frac{400}{7.2}\) = x
55.555… = x
56 ≈ x
It would take about 56 minutes to mow an area of 400 square feet.
Exercise 2.
A linear function has the table of values below. The information in the table shows the total volume of water, in gallons, that flows from a hose as a function of time, the number of minutes the hose has been running.

a. Describe the function in terms of volume and time.
Answer:
The total volume of water that flows from a hose is a function of the number of minutes the hose is left on.
b. Write the rule for the volume of water in gallons, y, as a linear function of time, x, given in minutes.
Answer:
y = \(\frac{44}{10}\) x
y = 4.4x
c. What number does the function assign to 250? That is, how many gallons of water flow from the hose during a period of 250 minutes?
Answer:
y = 4.4(250)
y = 1100
In 250 minutes, 1,100 gallons of water flow from the hose.
d. The average swimming pool holds about 17,300 gallons of water. Suppose such a pool has already been filled one quarter of its volume. Write an equation that describes the volume of water in the pool if, at time 0 minutes, we use the hose described above to start filling the pool.
Answer:
\(\frac{1}{4}\) (17300) = 4325
y = 4.4x + 4325
e. Approximately how many hours will it take to finish filling the pool?
Answer:
17300 = 4.4x + 4325
12975 = 4.4x
\(\frac{12975}{4.4}\) = x
2948.8636… = x
2949 ≈ x
\(\frac{2949}{60}\) = 49.15
It will take about 49 hours to fill the pool with the hose.
Exercise 3.
Recall that a linear function can be described by a rule in the form of y = mx + b, where m and b are constants. A particular linear function has the table of values below.

Answer:
a. What is the equation that describes the function?
Answer:
y = 5x + 4
b. Complete the table using the rule.
Answer:

Eureka Math Grade 8 Module 5 Lesson 3 Problem Set Answer Key
Question 1.
A food bank distributes cans of vegetables every Saturday. The following table shows the total number of cans they have distributed since the beginning of the year. Assume that this total is a linear function of the number of weeks that have passed.

a. Describe the function being considered in words.
Answer:
The total number of cans handed out is a function of the number of weeks that pass.
b. Write the linear equation that describes the total number of cans handed out, y, in terms of the number of weeks, x, that have passed.
Answer:
y = \(\frac{180}{1}\) x
y = 180x
c. Assume that the food bank wants to distribute 20,000 cans of vegetables. How long will it take them to meet that goal?
Answer:
20 000 = 180x
\(\frac{20000}{180}\) = x
111.1111… = x
111 ≈ x
It will take about 111 weeks to distribute 20,000 cans of vegetables, or about 2 years.
d. The manager had forgotten to record that they had distributed 35,000 cans on January 1. Write an adjusted linear equation to reflect this forgotten information.
Answer:
y = 180x + 35 000
e. Using your function in part (d), determine how long in years it will take the food bank to hand out 80,000 cans of vegetables.
Answer:
80 000 = 180x + 35 000
45 000 = 180x
\(\frac{45000}{180}\) = x
250 = x
To determine the number of years:
\(\frac{250}{52}\) = 4.8076… ≈ 4.8
It will take about 4.8 years to distribute 80,000 cans of vegetables.
Question 2.
A linear function has the table of values below. It gives the number of miles a plane travels over a given number of hours while flying at a constant speed.
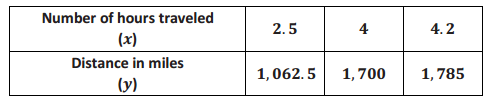
a. Describe in words the function given in this problem.
Answer:
The total distance traveled is a function of the number of hours spent flying.
b. Write the equation that gives the distance traveled, y, in miles, as a linear function of the number of hours, x, spent flying.
Answer:
y = \(\frac{1062.5}{2.5}\) x
y = 425x
c. Assume that the airplane is making a trip from New York to Los Angeles, which is a journey of approximately 2,475 miles. How long will it take the airplane to get to Los Angeles?
Answer:
2475 = 425x
\(\frac{2475}{425}\) = x
5.82352… = x
5.8 ≈ x
It will take about 5.8 hours for the airplane to fly 2,475 miles.
d. If the airplane flies for 8 hours, how many miles will it cover?
Answer:
y = 425(8)
y = 3400
The airplane would travel 3,400 miles in 8 hours.
Question 3.
A linear function has the table of values below. It gives the number of miles a car travels over a given number of hours.
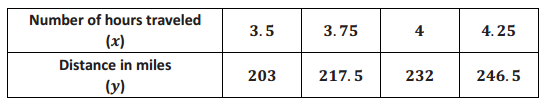
a. Describe in words the function given.
Answer:
The total distance traveled is a function of the number of hours spent traveling.
b. Write the equation that gives the distance traveled, in miles, as a linear function of the number of hours spent driving.
Answer:
y = \(\frac{203}{3.5}\) x
y = 58x
c. Assume that the person driving the car is going on a road trip to reach a location 500 miles from her starting point. How long will it take the person to get to the destination?
Answer:
500 = 58x
\(\frac{500}{58}\) = x
8.6206… = x
8.6 ≈ x
It will take about 8.6 hours to travel 500 miles.
Question 4.
A particular linear function has the table of values below.

a. What is the equation that describes the function?
Answer:
y = 3x + 1
b. Complete the table using the rule.
Answer:

Question 5.
A particular linear function has the table of values below.

a. What is the rule that describes the function?
Answer:
y = x + 6
b. Complete the table using the rule.
Answer:

Eureka Math Grade 8 Module 5 Lesson 3 Exit Ticket Answer Key
The information in the table shows the number of pages a student can read in a certain book as a function of time in minutes spent reading. Assume a constant rate of reading.

a. Write the equation that describes the total number of pages read, y, as a linear function of the number of minutes, x, spent reading.
Answer:
y = \(\frac{7}{2}\) x
y = 3.5x
b. How many pages can be read in 45 minutes?
Answer:
y = 3.5(45)
y = 157.5
In 45 minutes, the student can read 157.5 pages.
c. A certain book has 396 pages. The student has already read \(\frac{3}{8}\) of the pages and now picks up the book again at time x = 0 minutes. Write the equation that describes the total number of pages of the book read as a function of the number of minutes of further reading.
Answer:
\(\frac{3}{8}\) (396) = 148.5
y = 3.5x + 148.5
d. Approximately how much time, in minutes, will it take to finish reading the book?
Answer:
396 = 3.5x + 148.5
247.5 = 3.5x
\(\frac{247.5}{3.5}\) = x
70.71428571… = x
71 ≈ x
It will take about 71 minutes to finish reading the book.