Engage NY Eureka Math 8th Grade Module 3 Lesson 7 Answer Key
Eureka Math Grade 8 Module 3 Lesson 7 Exercise Answer Key
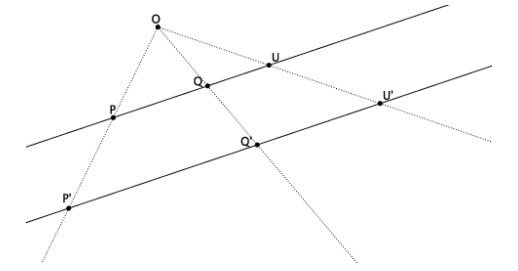
Use the diagram below to prove the theorem: Dilations preserve the measures of angles.
Let there be a dilation from center O with scale factor r. Given ∠PQR, show that since P’=Dilation(P),
Q’=Dilation(Q), and R’=Dilation(R), then |∠PQR|=|∠P’Q’R’|. That is, show that the image of the angle after a dilation has the same measure, in degrees, as the original.
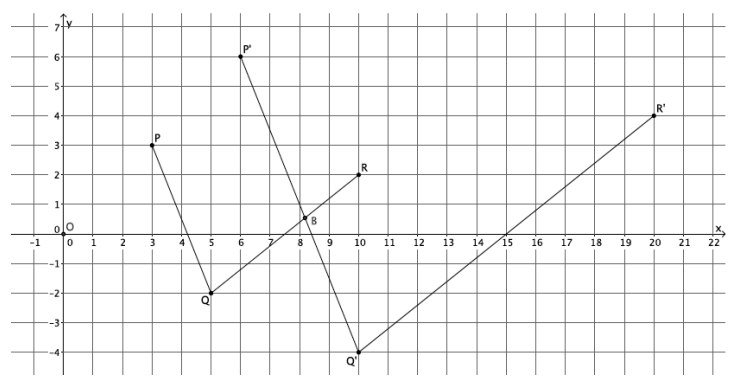
Answer:
Using FTS, we know that the line containing \(\overrightarrow{Q^{\prime} P^{\prime}}\) is parallel to the line containing \(\overrightarrow{Q P}\) and that the line containing \(\overrightarrow{Q R}\) is parallel to the line containing \(\overrightarrow{Q R}\). We also know that there exists just one line through a given point, parallel to a given line. Therefore, we know that ![]() must intersect
must intersect ![]() at a point. We know this because there is already a line that goes through point Q’ that is parallel to
at a point. We know this because there is already a line that goes through point Q’ that is parallel to ![]() , and that line is
, and that line is ![]() . Since
. Since ![]() cannot be parallel to
cannot be parallel to ![]() , it must intersect it. We let the intersection of
, it must intersect it. We let the intersection of ![]() and
and ![]() be named point B. Alternate interior angles of parallel lines cut by a transversal are equal in measure. Parallel lines QR and Q’R’ are cut by transversal \(\overline{\boldsymbol{Q}^{\prime} \boldsymbol{B}}\). Therefore, the alternate interior angles P’Q’R’ and Q’BQ are equal in measure. Parallel lines
be named point B. Alternate interior angles of parallel lines cut by a transversal are equal in measure. Parallel lines QR and Q’R’ are cut by transversal \(\overline{\boldsymbol{Q}^{\prime} \boldsymbol{B}}\). Therefore, the alternate interior angles P’Q’R’ and Q’BQ are equal in measure. Parallel lines ![]() and
and ![]() are cut by transversal \(\overline{Q B} .\) Therefore, the alternate interior angles PQR and Q’BQ are equal in measure. Since the measures of ∠P’Q’R’ and ∠PQR are equal to the measure of ∠QB’Q, then the measure of ∠PQR is equal to the measure of ∠P’ Q’ R’.
are cut by transversal \(\overline{Q B} .\) Therefore, the alternate interior angles PQR and Q’BQ are equal in measure. Since the measures of ∠P’Q’R’ and ∠PQR are equal to the measure of ∠QB’Q, then the measure of ∠PQR is equal to the measure of ∠P’ Q’ R’.
Eureka Math Grade 8 Module 3 Lesson 7 Problem Set Answer Key
Question 1.
A dilation from center O by scale factor r of a line maps to what? Verify your claim on the coordinate plane.
Answer:
The dilation of a line maps to a line.
Sample student work is shown below.
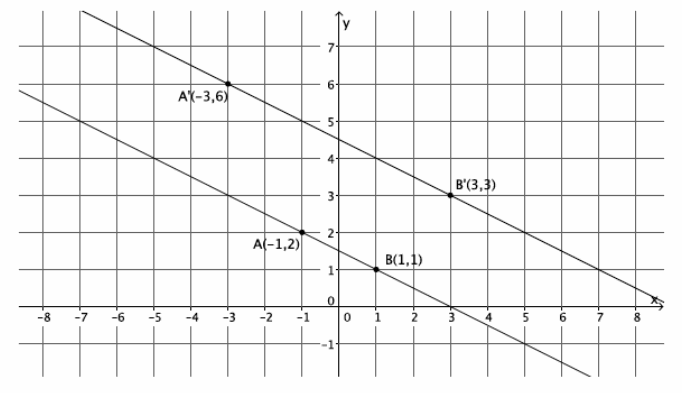
Question 2.
A dilation from center O by scale factor r of a segment maps to what? Verify your claim on the coordinate plane.
Answer:
The dilation of a segment maps to a segment.
Sample student work is shown below.
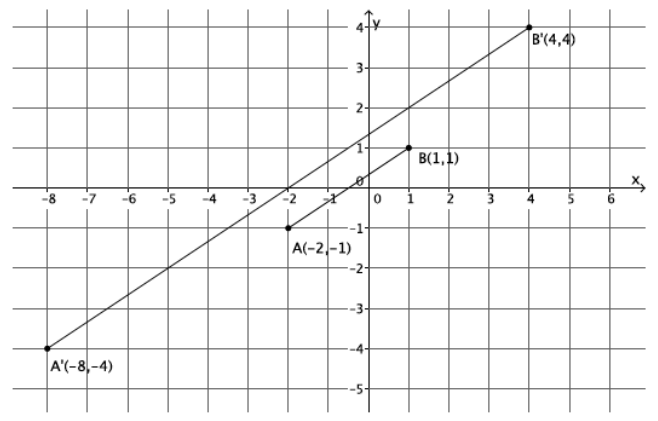
Question 3.
A dilation from center O by scale factor r of a ray maps to what? Verify your claim on the coordinate plane.
Answer:
The dilation of a ray maps to a ray.
Sample student work is shown below.
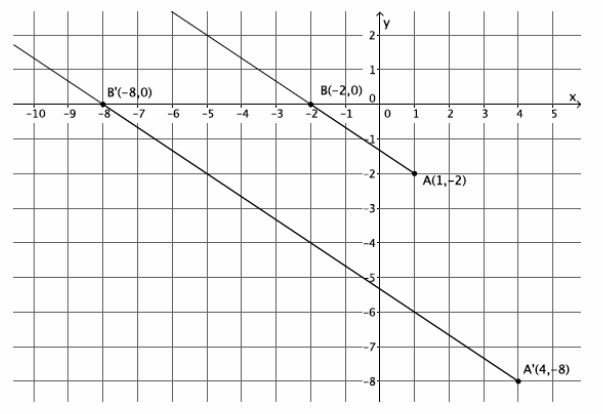
Question 4.
Challenge Problem:
Prove the theorem: A dilation maps lines to lines.
Let there be a dilation from center O with scale factor r so that P’=Dilation(P) and Q’=Dilation(Q). Show that line PQ maps to line P’Q’ (i.e., that dilations map lines to lines). Draw a diagram, and then write your informal proof of the theorem. (Hint: This proof is a lot like the proof for segments. This time, let U be a point on line PQ that is not between points P and Q.)
Answer:
Sample student drawing and response are below:
Let U be a point on line PQ. By the definition of dilation, we also know that U’=Dilation(U). We need to show that U’ is a point on line P’Q’. If we can, then we have proven that a dilation maps lines to lines.
By the definition of dilation and FTS, we know that \(\frac{\left|O P^{\prime}\right|}{|O P|}\) =\(\frac{\left|O Q^{\prime}\right|}{|O Q|}\) and that \(\overleftrightarrow{P Q}\) is parallel to ![]() . Similarly, we know that
. Similarly, we know that  and that line QU is parallel to line Q’U’. Since U is a point on line PQ, then we also know that line PQ is parallel to line Q’U’. But we already know that
and that line QU is parallel to line Q’U’. Since U is a point on line PQ, then we also know that line PQ is parallel to line Q’U’. But we already know that ![]() is parallel to
is parallel to ![]() . Since there can only be one line that passes through Q’ that is parallel to line PQ, then line P’Q’ and line Q’U’ must coincide. That places the dilation of point U, U’, on the line P’Q’, which proves that dilations map lines to lines.
. Since there can only be one line that passes through Q’ that is parallel to line PQ, then line P’Q’ and line Q’U’ must coincide. That places the dilation of point U, U’, on the line P’Q’, which proves that dilations map lines to lines.
Eureka Math Grade 8 Module 3 Lesson 7 Exit Ticket Answer Key
Dilate ∠ABC with center O and scale factor r=2. Label the dilated angle, ∠A’B’C’.
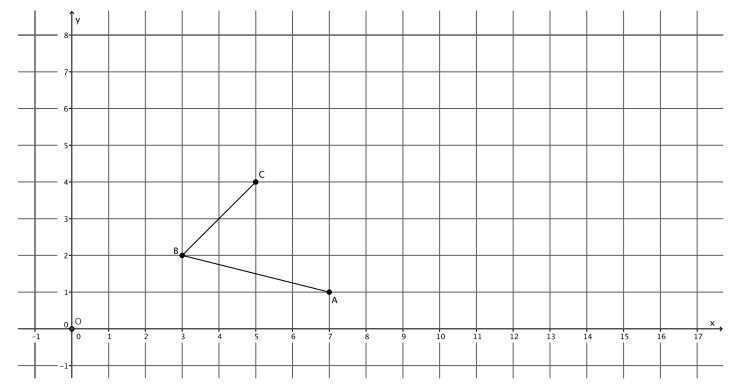
Answer:
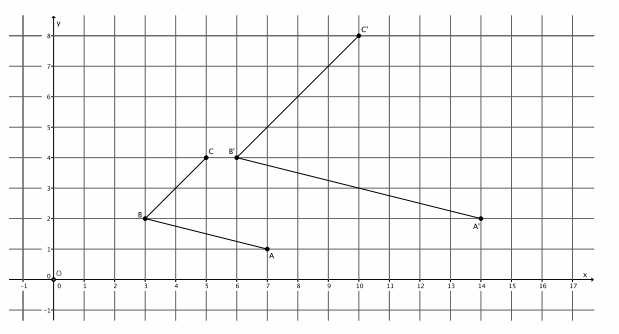
Question 1.
If ∠ABC=72°, then what is the measure of ∠A’ B’ C’?
Answer:
Since dilations preserve angles, then ∠A’B’C’=72°.
Question 2.
If the length of segment AB is 2 cm, what is the length of segment A’B’?
Answer:
The length of segment A’B’ is 4 cm.
Question 3.
Which segments, if any, are parallel?
Answer:
Since dilations map segments to parallel segments, then \(\overline{A B}\) || \(\overline{A^{\prime} B^{\prime}}\), and \(\overline{\boldsymbol{B C}}\) || \(\overline{\boldsymbol{B}^{\prime} \boldsymbol{C}^{\prime}}\).