Engage NY Eureka Math 8th Grade Module 2 Lesson 13 Answer Key
Eureka Math Grade 8 Module 2 Lesson 13 Exploratory Challenge Answer Key
Classwork
Concept Development
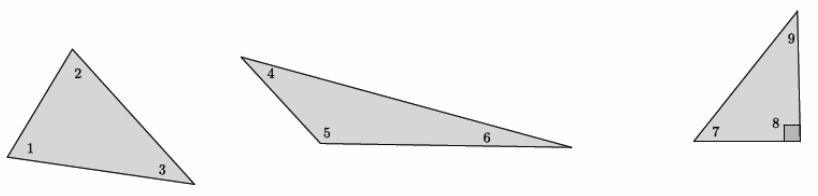
m∠1+m∠2+m∠3=m∠4+m∠5+m∠6=m∠7+m∠8+m∠9=180°
Note that the sum of the measures of angles 7 and 9 must equal 90° because of the known right angle in the right triangle.
We want to prove that the angle sum of any triangle is 180°. To do so, we use some facts that we already know about geometry:
→ A straight angle is 180° in measure.
→ Corresponding angles of parallel lines are equal in measure (corr. ∠’s, \(\overline{A B}\) || \(\overline{C D}\).
→ Alternate interior angles of parallel lines are equal in measure (alt. ∠’s, \(\overline{A B}\) || \(\overline{C D}\).
Exploratory Challenge 1.
Let triangle ABC be given. On the ray from B to C, take a point D so that C is between B and D. Through point C, draw a segment parallel to \(\overline{A B}\), as shown. Extend the segments AB and CE. Line AC is the transversal that intersects the parallel lines.
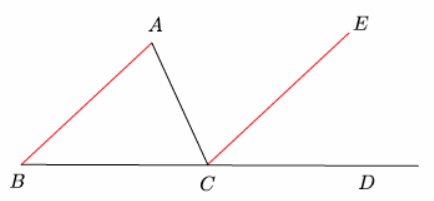
a. Name the three interior angles of triangle ABC.
Answer:
∠ABC, ∠BAC, ∠BCA
b. Name the straight angle.
Answer:
∠BCD
Our goal is to show that the measures of the three interior angles of triangle ABC are equal to the measures of the angles that make up the straight angle. We already know that a straight angle is 180° in measure.
If we can show that the interior angles of the triangle are the same as the angles of the straight angle, then we will have proven that the sum of the measures of the interior angles of the triangle have a sum of 180°.
c. What kinds of angles are ∠ABC and ∠ECD? What does that mean about their measures?
Answer:
∠ABC and ∠ECD are corresponding angles. Corresponding angles of parallel lines are equal in measure (corr. ∠’s, \(\overline{A B}\) || \(\overline{\boldsymbol{C E}}\)).
d. What kinds of angles are ∠BAC and ∠ECA? What does that mean about their measures?
Answer:
∠BAC and ∠ECA are alternate interior angles. Alternate interior angles of parallel lines are equal in measure (alt. ∠’s, \(\overline{\boldsymbol{A B}}\) || \(\overline{\boldsymbol{C E}}\)).
d. We know that m∠BCD=m∠BCA+m∠ECA+m∠ECD=180°. Use substitution to show that the measures of the three interior angles of the triangle have a sum of 180°.
Answer:
m∠BCD=m∠BCA+m∠BAC+m∠ABC=180° (∠ sum of △)
Exploratory Challenge 2.
The figure below shows parallel lines L1 and L2 . Let m and n be transversals that intersect L1 at points B and C, respectively, and L2 at point F, as shown. Let A be a point on L1 to the left of B, D be a point on L1 to the right of C, G be a point on L2 to the left of F, and E be a point on L2 to the right of F.
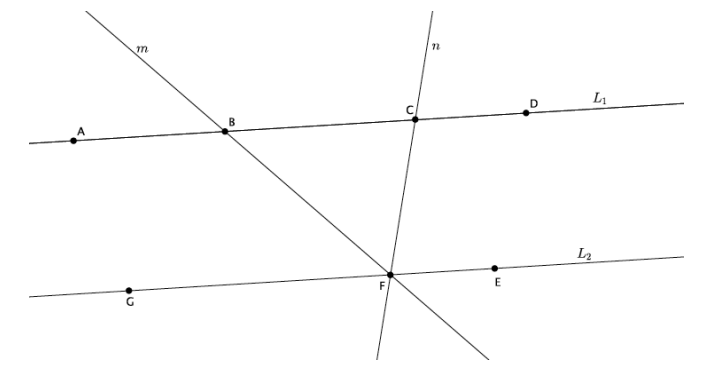
a. Name the triangle in the figure.
Answer:
△BCF
b. Name a straight angle that will be useful in proving that the sum of the measures of the interior angles of the triangle is 180°.
Answer:
∠GFE
As before, our goal is to show that the sum of the measures of the interior angles of the triangle are equal to the measure of the straight angle. Use what you learned from Exploratory Challenge 1 to show that the measures of the interior angles of a triangle have a sum of 180°.
c. Write your proof below.
Answer:
The straight angle ∠GFE is comprised of ∠GFB, ∠BFC, and ∠EFC. Alternate interior angles of parallel lines are equal in measure (alt. ∠’s, \(\overline{A D}\) || \(\overline{C E}\)). For that reason, ∠BCF=∠EFC and ∠CBF=∠GFB. Since ∠GFE is a straight angle, it is equal to 180°. Then, ∠GFE=∠GFB+∠BFC+∠EFC=180°.
By substitution, ∠GFE=∠CBF+∠BFC+∠BCF=180°. Therefore, the sum of the measures of the interior angles of a triangle is 180° (∠ sum of △).
Eureka Math Grade 8 Module 2 Lesson 13 Exit Ticket Answer Key
Question 1.
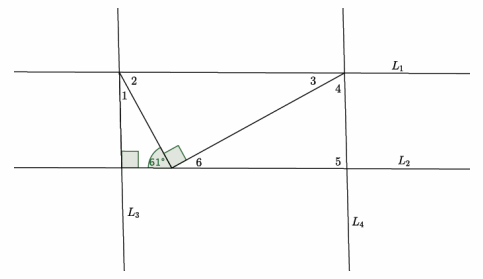
If L1 || L2 , and L3 || L4 , what is the measure of ∠1? Explain how you arrived at your answer.
Answer:
The measure of angle 1 is 29°. I know that the angle sum of triangles is 180°. I already know that two of the angles of the triangle are 90° and 61°.
Question 2.
Given that line AB is parallel to line CE, present an informal argument to prove that the measures of the interior angles of triangle ABC have a sum of 180°.
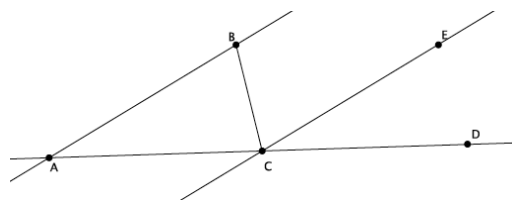
Answer:
Since \(\overleftrightarrow{A B}\) is parallel to \(\overleftrightarrow{C E}\), the corresponding angles ∠BAC and ∠ECD are equal in measure. Similarly, ∠ABC and ∠ECB are equal in measure because they are alternate interior angles. Since ∠ACD is a straight angle (i.e., equal to 180° in measure), substitution shows that triangle ABC has a sum of 180°. Specifically, the straight angle is made up of ∠ACB, ∠ECB, and ∠ECD. ∠ACB is one of the interior angles of the triangle and one of the angles of the straight angle. We know that ∠ABC has the same measure as ∠ECB and that ∠BAC has the same measure as ∠ECD. Therefore, the sum of the measures of the interior angles will be the same as the sum of the measures of the angles of the straight angle, which is 180°.
Eureka Math Grade 8 Module 2 Lesson 13 Problem Set Answer Key
Students practice presenting informal arguments about the sum of the angles of a triangle using the theorem to find the measures of missing angles.
Question 1.
In the diagram below, line AB is parallel to line CD, that is, LAB ∥LCD. The measure of ∠ABC is 28° and the measure of ∠EDC is 42°. Find the measure of ∠CED. Explain why you are correct by presenting an informal argument that uses the angle sum of a triangle.
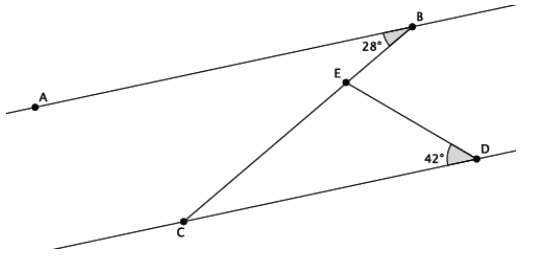
Answer:
The measure of ∠CED is 110°. This is the correct measure for the angle because ∠ABC and ∠DCE are alternate interior angles of parallel lines. That means that the angles are congruent and have the same measure. Since the angle sum of a triangle is 180°, then ∠CED=180°-(28°+42°) and ∠CED is 110°.
Question 2.
In the diagram below, line AB is parallel to line CD, that is, LAB || LCD . The measure of ∠ABE is 38°, and the measure of ∠EDC is 16°. Find the measure of ∠BED. Explain why you are correct by presenting an informal argument that uses the angle sum of a triangle. (Hint: Find the measure of ∠CED first, and then use that measure to find the measure of ∠BED.)
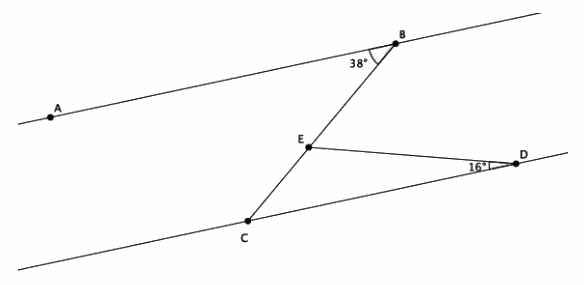
Answer:
The measure of ∠BED is 54°. This is the correct measure for the angle because ∠ABC and ∠DCE are alternate interior angles of parallel lines. That means that the angles are congruent and have the same measure. Since the angle sum of a triangle is 180°, then ∠CED=180°-(38°+16°)=126°. The straight angle ∠BEC is made up of ∠CED and ∠BED. Since we know straight angles measure 180° and ∠CED=126°, then ∠BED is 54°.
Question 3.
In the diagram below, line AB is parallel to line CD, that is, LAB || LCD . The measure of ∠ABE is 56°, and the measure of ∠EDC is 22°. Find the measure of ∠BED. Explain why you are correct by presenting an informal argument that uses the angle sum of a triangle. (Hint: Extend the segment BE so that it intersects line CD.)
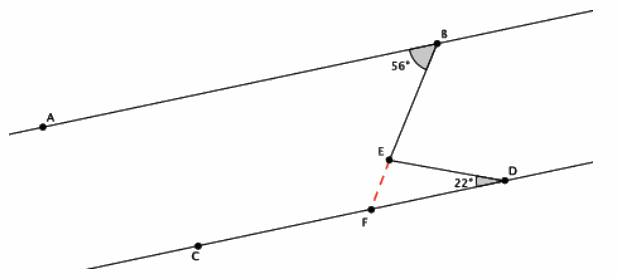
Answer:
The measure of ∠BED is 78°. This is the correct measure for the angle because ∠ABE and ∠DFE are alternate interior angles of parallel lines. That means that the angles are congruent and have the same measure. Since the angle sum of a triangle is 180°, then ∠FED=180°-(56°+22°)=102°. The straight angle ∠BEF is made up of ∠FED and ∠BED. Since straight angles measure 180° and ∠FED is 102°, then ∠BED is 78°.
Question 4.
What is the measure of ∠ACB?
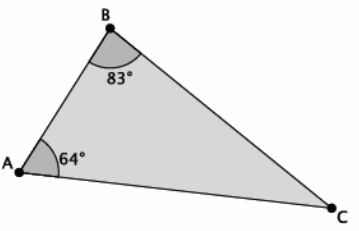
Answer:
The measure of ∠ACB is 180°-(83°+64°), which is equal to 33°.
Question 5.
What is the measure of ∠EFD?
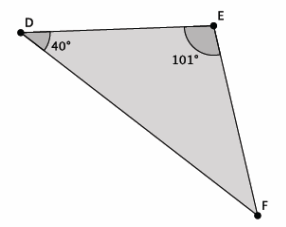
Answer:
The measure of ∠EFD is 180°-(101°+40°), which is equal to 39°.
Question 6.
What is the measure of ∠HIG?
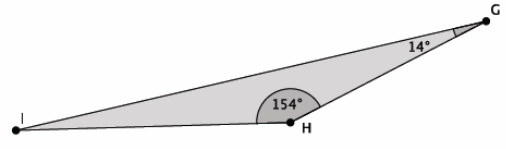
Answer:
The measure of ∠HIG is 180°-(154°+14°), which is equal to 12°.
Question 7.
What is the measure of ∠ABC?
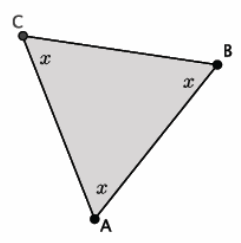
Answer:
The measure of ∠ABC is 60° because 60°+60°+60°, which is equal to 180°.
Question 8.
Triangle DEF is a right triangle. What is the measure of ∠EFD?
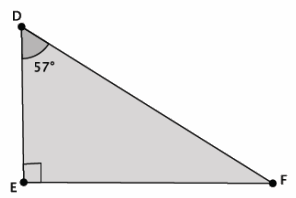
Answer:
The measure of ∠EFD is 90°-57°, which is equal to 33°.
Question 9.
In the diagram below, Lines L1 and L2 are parallel. Transversals r and s intersect both lines at the points shown below. Determine the measure of ∠JMK. Explain how you know you are correct.
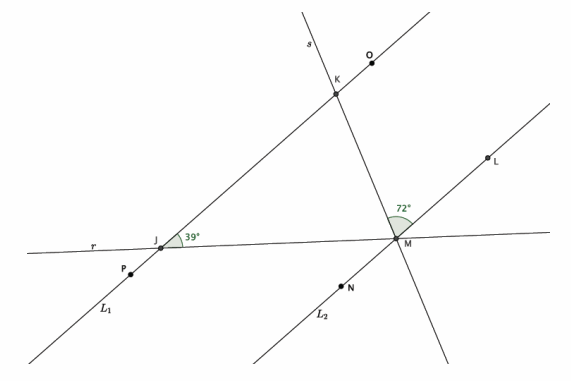
Answer:
The Lines L1 and L2 are parallel, which means that the alternate interior angles formed by the transversals are equal. Specifically, ∠LMK=∠JKM=72°. Since △JKM has a sum of interior angles equal to 180°,
∠KJM+∠JMK+∠JKM=180°. By substitution, we have 39°+∠JMK+72°=180°; therefore, ∠JMK is 69°.