Eureka Math Grade 8 Module 7 Lesson 2 Answer Key

Engage NY Eureka Math 8th Grade Module 7 Lesson 2 Answer Key

Eureka Math Grade 8 Module 7 Lesson 2 Exercise Answer Key

Exercise 1.
Determine the positive square root of 81, if it exists. Explain.
Answer:
The square root of 81 is 9 because 9²=81.

Exercise 2.
Determine the positive square root of 225, if it exists. Explain.
Answer:
The square root of 225 is 15 because 15²=225.

Exercise 3.
Determine the positive square root of -36, if it exists. Explain.
Answer:
The number -36 does not have a square root because there is no number squared that can produce a negative number.

Exercise 4.
Determine the positive square root of 49, if it exists. Explain.
Answer:
The square root of 49 is 7 because 7²=49.

Discussion

Answer:
Place the numbers \(\sqrt{1}\), \(\sqrt{4}\), \(\sqrt{9}\), and \(\sqrt{1}\)6 on the number line, and explain how you knew where to place them.
Solutions are shown below in red.

Place the numbers \(\sqrt{2}\) and \(\sqrt{3}\) on the number line. Be prepared to explain your reasoning.
Solutions are shown below in red. Students should reason that the numbers \(\sqrt{2}\) and \(\sqrt{3}\) belong on the number line between \(\sqrt{1}\) and \(\sqrt{4}\). They might be more specific and suggest that the numbers \(\sqrt{2}\) and \(\sqrt{3}\) sit equally spaced in the interval between 1 and 2. This idea suggests that 1 \(\frac{1}{3}\) might be a good approximation for \(\sqrt{2}\) and 1 \(\frac{2}{3}\) for \(\sqrt{3}\). Of course, this suggested spacing is just speculation for now.

Place the numbers \(\sqrt{5}\), \(\sqrt{6}\), \(\sqrt{7}\), and \(\sqrt{8}\) on the number line. Be prepared to explain your reasoning.
Solutions are shown below in red. The discussion about placement should be similar to the previous one.

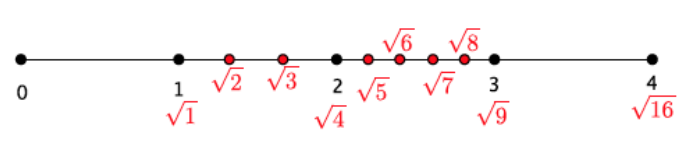
Place the numbers \(\sqrt{1}\)0, \(\sqrt{1}\)1, \(\sqrt{1}\)2, \(\sqrt{1}\)3, \(\sqrt{1}\)4, and \(\sqrt{1}\)5 on the number line. Be prepared to explain your reasoning.
Solutions are shown below in red. The discussion about placement should be similar to the previous one.

Our work on the number line shows that there are many more square roots of whole numbers that are not perfect squares than those that are perfect squares. On the number line above, we have four perfect square numbers and twelve that are not! After we do some more work with roots, in general, we will cover exactly how to describe these numbers and how to approximate their values with greater precision. For now, we will estimate their locations on the number line using what we know about perfect squares.

Determine the positive square root of the number given. If the number is not a perfect square, determine which whole number the square root would be closest to, and then use guess and check to give an approximate answer to one or two decimal places.
Exercise 5.
\(\sqrt{49}\)
Answer:
7

Exercise 6.
\(\sqrt{62}\)
Answer:
The square root of 62 is close to 8. The square root of 62 is approximately 7.9 because 7.9²=62.41.

Exercise 7.
\(\sqrt{122}\)
Answer:
The square root of 122 is close to 11. Students may guess a number between 11 and 11.1 because 11.05²=122.1025.

Exercise 8.
\(\sqrt{400}\)
Answer:
20

Exercise 9.
Which of the numbers in Exercises 5–8 are not perfect squares? Explain.
Answer:
The numbers 62 and 122 are not perfect squares because there is no integer x to satisfy x²=62 or x²=122.

Eureka Math Grade 8 Module 7 Lesson 2 Problem Set Answer Key

Determine the positive square root of the number given. If the number is not a perfect square, determine the integer to which the square root would be closest.
Question 1.
\(\sqrt{169}\)
Answer:
13

Question 2.
\(\sqrt{256}\)
Answer:
16

Question 3.
\(\sqrt{81}\)
Answer:
9

Question 4.
\(\sqrt{147}\)
Answer:
The number 147 is not a perfect square. It is between the perfect squares 144 and 169 but closer to 144. Therefore, the square root of 147 is close to 12.

Question 5.
\(\sqrt{8}\)
Answer:
The number 8 is not a perfect square. It is between the perfect squares 4 and 9 but closer to 9. Therefore, the square root of 8 is close to 3.

Question 6.
Which of the numbers in Problems 1–5 are not perfect squares? Explain.
Answer:
The numbers 147 and 8 are not perfect squares because there is no integer x so that x²=147 or x²=8.

Question 7.
Place the following list of numbers in their approximate locations on a number line.
\(\sqrt{32}\), \(\sqrt{12}\), \(\sqrt{27}\), \(\sqrt{18}\), \(\sqrt{23}\), and \(\sqrt{50}\)
Answer:
Answers are noted in red.

Question 8.
Between which two integers will \(\sqrt{45}\) be located? Explain how you know.
Answer:
The number 45 is not a perfect square. It is between the perfect squares 36 and 49 but closer to 49. Therefore, the square root of 45 is between the integers 6 and 7 because \(\sqrt{36}\) = 6 and \(\sqrt{49}\) = 7 and \(\sqrt{36}\) < \(\sqrt{45}\) < \(\sqrt{49}\).

Eureka Math Grade 8 Module 7 Lesson 2 Exit Ticket Answer Key

Question 1.
Write the positive square root of a number x in symbolic notation.
Answer:
\(\sqrt{x}\)

Question 2.
Determine the positive square root of 196. Explain.
Answer:
\(\sqrt{196}\) = 14 because 14² = 196.

Question 3.
The positive square root of 50 is not an integer. Which whole number does the value of \(\sqrt{50}\) lie closest to? Explain.
Answer:
\(\sqrt{50}\) is between 7 and 8 but closer to 7. The reason is that 7²=49, and 8²=64. The number 50 is between 49 and 64 but closer to 49. Therefore, the square root of 50 is close to 7.

Question 4.
Place the following numbers on the number line in approximately the correct positions: \(\sqrt{16}\), \(\sqrt{9}\), \(\sqrt{11}\), and 3.5.

Answer:
Solutions are shown in red below.