Engage NY Eureka Math 7th Grade Module 6 Lesson 18 Answer Key
Eureka Math Grade 7 Module 6 Lesson 18 Example Answer Key
Example 1.
With your group, discuss whether a right rectangular prism can be sliced at an angle so that the resulting slice looks like the figure in Figure 1. If it is possible, draw an example of such a slice into the following prism.
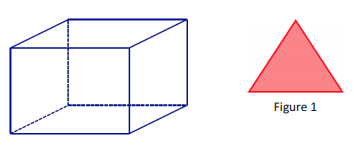
Answer:
Once students have had some time to attempt Example 1, pose the following questions:
→ Is it possible to make a triangular slice from this prism? Where would this slice have to be made? Students may choose their method of how to represent the slice (e.g., drawing a 2D or 3D sketch or describing the slice in words).
→ Yes, it is possible. It can be done by slicing off a corner of the right rectangular prism.
Here, and elsewhere, some students may be able to visualize this right away, while others may struggle.
Allow some time to see if any one group has a valid answer. If there is a valid answer, use it for the next item; otherwise, share the following triangular slice of a right rectangular prism.
→ Here is a slice that results in a triangular region. Does this triangle have three equal sides, two equal sides, or no equal sides?
Encourage students to use a ruler to verify their answers.
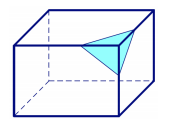
→ The slice is a triangle with no equal sides.
→ At how many points does the slice meet an edge of the right rectangular prism? What makes these points important with respect to the triangle?
→ The slice meets an edge of the right rectangular prism at three points, one on each of three edges; these three points are the vertices of the triangle.
→ Find another slice that will create another scalene triangular region. Mark the vertices on the edges of the prism.
Example 2.
With your group, discuss whether a right rectangular prism can be sliced at an angle so that the resulting slice looks like the figure in Figure 4. If it is possible, draw an example of such a slice into the following prism.
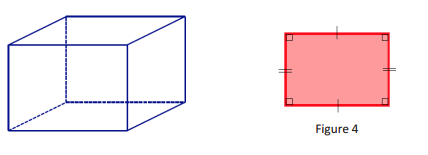
Answer:
Once students have had some time to attempt Example 2, pose the following questions:
→ Is it possible to slice this right rectangular prism to form a quadrilateral cross section? Remember, we are slicing at an angle now. Consider what you know about vertices and the edges they fall on from Example 1.
Again, some students may be able to visualize this right away, while some might not. Give students time to experiment with the solution. Use a valid response to the question to move forward, or simply share the image provided.
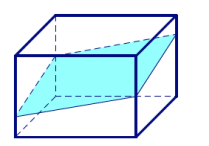
→ Here is one possible slice in the shape of a quadrilateral. Notice that the slice is, in fact, made by a plane.
A common error, especially when outlining a quadrilateral slice by its vertices, is to make a slice that is not a true slice because the figure could not be made by a single plane.
→ What must be true about the opposite sides of the quadrilateral?
→ The opposite sides are parallel.
The conclusion that the opposite sides of the quadrilateral region are parallel is based on the above image. This conclusion likely comes from their understanding that the opposite faces of the right rectangular prism are parallel. Therefore, since the opposite sides lie in these faces, they too must be parallel.
This might be an appropriate time to show them an image like the following:
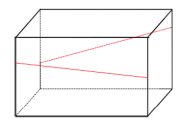
→ Though the segments lie in planes that are a constant distance apart, the segments are not parallel.
→ Because the earlier slice is made by one plane, the segments that form the sides of the quadrilateral-shaped slice both lie in the same plane as each other and in opposite faces that are an equal distance apart. Together, this means the segments are parallel.
→ Not only is this slice a quadrilateral, but it is a special quadrilateral. What kind of special quadrilateral-shaped slice must it be?
→ Since we have determined the opposite sides of the quadrilateral to be parallel, the quadrilateral must be a parallelogram.
Have students draw another example of a slice through the right rectangular prism that results in a parallelogram shape.
Example 3.
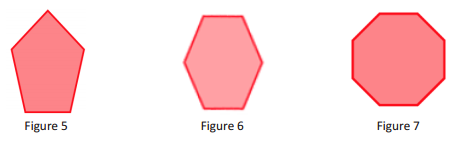
a. If slicing a plane through a right rectangular prism so that the slice meets the three faces of the prism, the resulting slice is in the shape of a triangle; if the slice meets four faces, the resulting slice is in the shape of a quadrilateral. Is it possible to slice the prism in a way that the region formed is a pentagon (as in Figure 5)? A hexagon (as in Figure 6)? An octagon (as in Figure 7)?
b. Draw an example of a slice in a pentagon shape and a slice in a hexagon shape.
Answer:
a. Yes, it is possible to slice a right rectangular prism with a plane so that the resulting cross section is a pentagon; the slice would have to meet five of the six faces of the prism. Similarly, it is possible for the slice to take the shape of a hexagon if the slice meets all six faces. It is impossible to create a slice in the shape of an octagon because a right rectangular prism has six faces, and it is not possible for the shape of a slice to have more sides than the number of faces of the solid.
b. 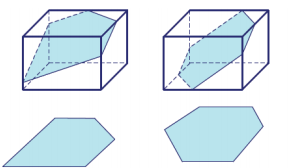
Example 4.
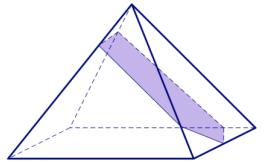
a. With your group, discuss whether a right rectangular pyramid can be sliced at an angle so that the resulting slice looks like the figure in Figure 8. If it is possible, draw an example of such a slice into the following pyramid.
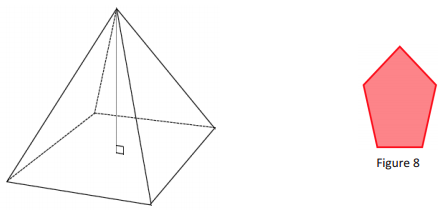
b. With your group, discuss whether a right rectangular pyramid can be sliced at an angle so that the resulting slice looks like the figure in Figure 9. If it is possible, draw an example of such a slice into the pyramid above.
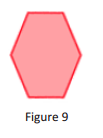
Answer:
Allow students time to experiment with this slice. Remind students that marking the vertices of the slice on the edges of the pyramid facilitates the drawing of the slice.
If there is no valid response, share the figure below.
Ask students to find a second slice in the shape of a pentagon.
b. It is impossible to create a slice in the shape of a hexagon because a right rectangular pyramid has five faces, and it is not possible for the shape of a slice to have more sides than the number of faces of the solid.
Eureka Math Grade 7 Module 6 Lesson 18 Exercise Answer Key
Exercise 1.
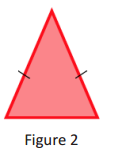
a. With your group, discuss how to slice a right rectangular prism so that the resulting slice looks like the figure in Figure 2. Justify your reasoning.
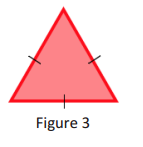
b. With your group, discuss how to slice a right rectangular prism so that the resulting slice looks like the figure in Figure 3. Justify your reasoning.
Answer:
a. I would use a ruler to measure two segments of equal length on two edges that meet at a common vertex. Then, I would join these two endpoints with a third segment.
b. I would use a ruler to measure three segments of equal length on three edges that meet at a common vertex.
Exercise 2.
In Example 2, we discovered how to slice a right rectangular prism to makes the shapes of a rectangle and a parallelogram. Are there other ways to slice a right rectangular prism that result in other quadrilateral-shaped slices?
Answer:
Allow students more time to experiment with other possible slices that might result in another kind of quadrilateral.
If there is no valid response, share the figure below.
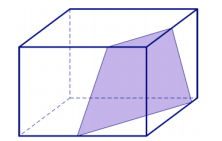
A slice can be made to a right rectangular prism at an angle so that the resulting cross section is a trapezoid
(as in the example shown above). In addition to slicing at an angle, it is also possible to slice perpendicular to a face or base to form a trapezoid-shaped slice.
Eureka Math Grade 7 Module 6 Lesson 18 Problem Set Answer Key
Question 1.
Draw a slice into the right rectangular prism at an angle in the form of the provided shape, and draw each slice as a 2D shape.
Answer:
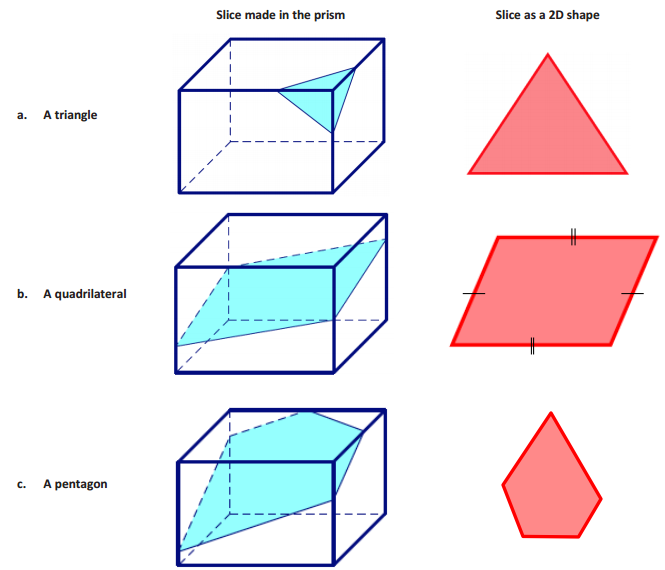
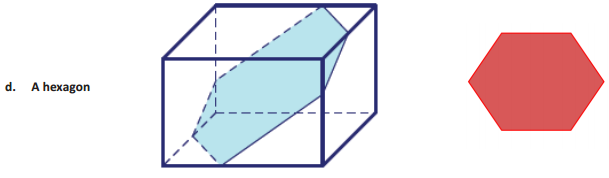
Question 2.
Draw slices at an angle in the form of each given shape into each right rectangular pyramid, and draw each slice as a 2D shape.
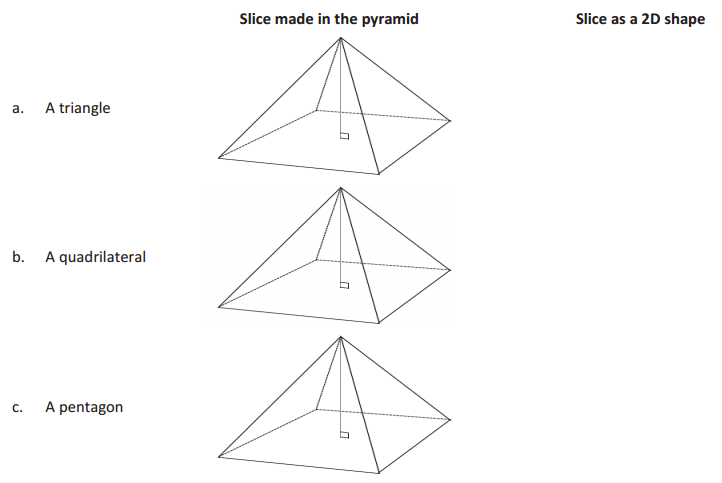
Answer:
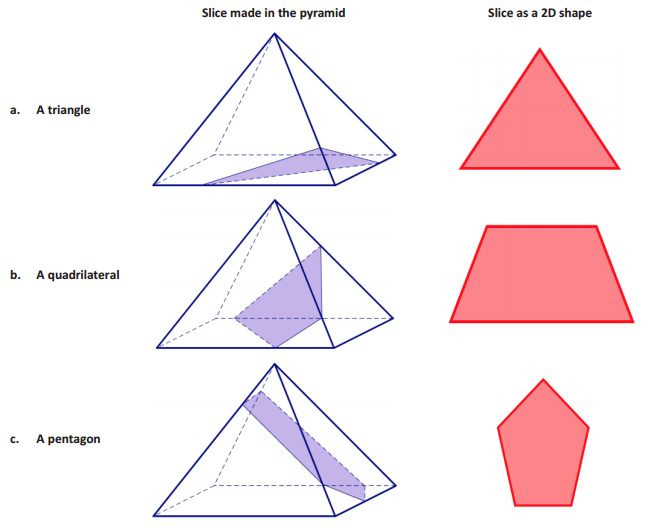
Question 3.
Why is it not possible to draw a slice in the shape of a hexagon for a right rectangular pyramid?
Answer:
It is not possible for the shape of a slice to have more sides than the number of faces of the solid.
Question 4.
If the slicing plane meets every face of a right rectangular prism, then the slice is a hexagonal region. What can you say about opposite sides of the hexagon?
Answer:
The opposite sides of the hexagon lie in opposite faces; therefore, they are parallel.
Question 5.
Draw a right rectangular prism so that rectangles ABCD and A’B’C’D’ are base faces. The line segments AA’, BB’, CC’, and DD’ are edges of the lateral faces.
a. A slicing plane meets the prism so that vertices A, B, C, and D lie on one side of the plane, and vertices A’, B’, C’, and D’ lie on the other side. Based on the slice’s position, what other information can be concluded about the slice?
b. A slicing plane meets the prism so that vertices A, B, C, and B’ are on one side of the plane, and vertices A’, D’, C’, and D are on the other side. What other information can be concluded about the slice based on its position?
Answer:
a. The slice misses the base faces ABCD and A’B’C’D’ since all the vertices of each face lie on the same side of the plane. The slice meets each of the lateral faces in an interval since each lateral face has two vertices on each side. The slice is a quadrilateral. In fact, the slice is a parallelogram because opposite faces of a right rectangular prism lie in parallel planes.
b. The slice meets each face in line segments because, in each case, three of the vertices of the face are on one side of the plane and the remaining vertex lies in the opposite side. The slice is a hexagon because it has six edges. Opposite sides of the hexagon are parallel since they lie in parallel planes.
Eureka Math Grade 7 Module 6 Lesson 18 Exit Ticket Answer Key
Question 1.
Draw a slice that has the maximum possible number of sides for each solid. Explain how you got your answer.
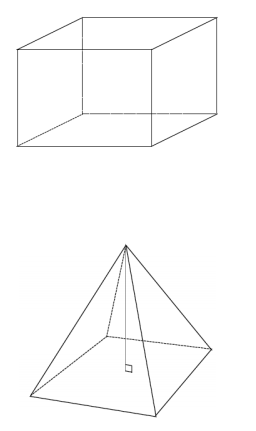
Answer:
The slice in the right rectangular prism should be hexagonal (diagrams will vary); the slice in the right rectangular pyramid should be pentagonal (again, diagrams will vary).
The edges of a slice are determined by the number of faces the slicing plane meets; there cannot be more sides to the polygon than there are faces of the solid.