Engage NY Eureka Math 7th Grade Module 6 Lesson 17 Answer Key
Eureka Math Grade 7 Module 6 Lesson 17 Example Answer Key
Example 1.
Use the models you built to assist in a sketch of a pyramid. Though you are sketching from a model that is opaque, use dotted lines to represent the edges that cannot be seen from your perspective.
Answer:
Sketches will vary; emphasize the distinction between the pyramids by asking how each must be drawn.
Students may struggle with this example; remind them that attempting these sketches is not a test of artistic ability but rather an exercise in becoming more familiar with the structure of a pyramid. They are working toward visualizing how a plane slices a rectangular pyramid perpendicular and parallel to its base.
Example 2.
Sketch a right rectangular pyramid from three vantage points: (1) from directly over the vertex, (2) from facing straight on to a lateral face, and (3) from the bottom of the pyramid. Explain how each drawing shows each view of the pyramid.
Answer:
Possible sketches:
1. From directly overhead, all four lateral faces are visible.
2. From facing a lateral face, the one entire lateral face is visible, as well as a bit of the adjacent lateral faces. If the pyramid were transparent, I would be able to see the entire base.
3. From the bottom, only the rectangular base is visible.
Example 3.
Assume the following figure is a top-down view of a rectangular pyramid. Make a reasonable sketch of any two adjacent lateral faces. What measurements must be the same between the two lateral faces? Mark the equal measurement. Justify your reasoning for your choice of equal measurements.
Answer:
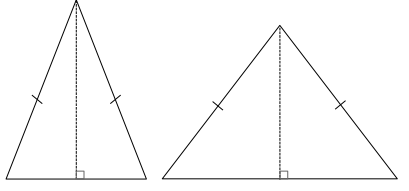
The equal sides in each triangle are the same between both triangles.
Students may think that the heights of the triangles are equal in length, when in fact they are not, unless the base is a square. The triangle with the shorter base has a height greater than that of the triangle with the longer base.
An easy way of making this point is by looking at a right rectangular pyramid with a rectangular base of exaggerated dimensions: a very long length in contrast to a very short width. Though students do not yet have the Pythagorean theorem at their disposal to help them quantify the difference in heights of the lateral faces, an image should be sufficiently persuasive.
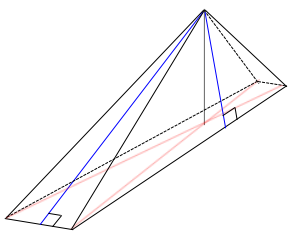
Example 4.
a. A slicing plane passes through segment a parallel to base B of the right rectangular pyramid below. Sketch what the slice will look like into the figure. Then sketch the resulting slice as a two-dimensional figure. Students may choose how to represent the slice (e.g., drawing a 2D or 3D sketch or describing the slice in words).
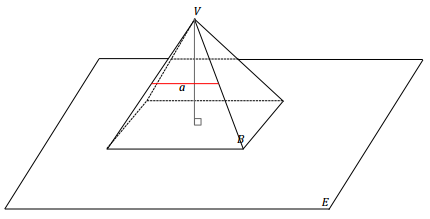
b. What shape does the slice make? What is the relationship between the slice and the rectangular base of the pyramid?
Answer:
a. 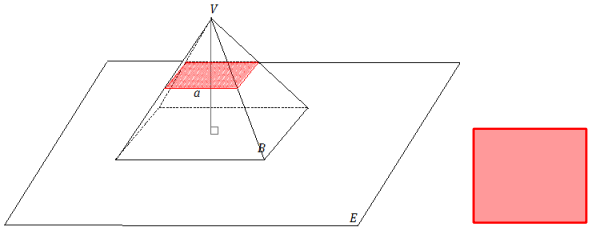
b. The slice is a rectangle; the slice looks a lot like the rectangular base but is smaller in size.
Example 5.
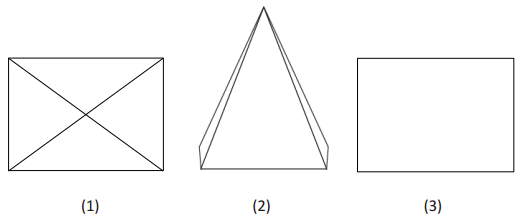
A slice is to be made along segment a perpendicular to base B of the right rectangular pyramid below.
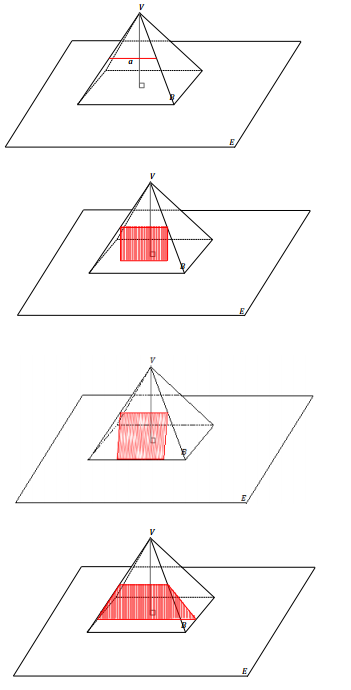
a. Which of the following figures shows the correct slice? Justify why each of the following figures is or is not a correct diagram of the slice.
b. A slice is taken through the vertex of the pyramid perpendicular to the base. Sketch what the slice will look like into the figure. Then, sketch the resulting slice itself as a two-dimensional figure.
Answer:
a. 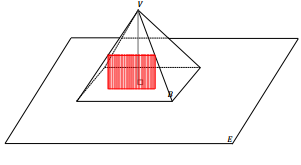
This is not a slice by a plane because there is space between the base and the lateral face. This could be a slice by a rectangle with the same width as in the figure but not a plane that extends in all directions.
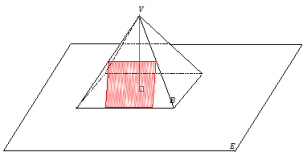
This is not a slice by a plane perpendicular to the base because the marked rectangular region is in the same plane as the lateral face in which it lies.
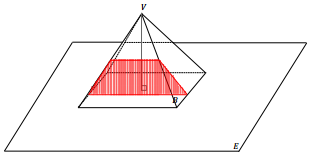
This is a slice made by a plane meeting the rectangular pyramid perpendicular to its base. The slice shows all the possible points at which the slicing plane would make contact with the right rectangular pyramid. The slice is in the shape of an isosceles trapezoid.
b. A slice is taken through the vertex of the pyramid perpendicular to the base. Sketch what the slice will look like into the figure. Then, sketch the resulting slice itself as a two-dimensional figure.
Eureka Math Grade 7 Module 6 Lesson 17 Problem Set Answer Key
Question 1.
A side view of a right rectangular pyramid is given. The line segments lie in the lateral faces.
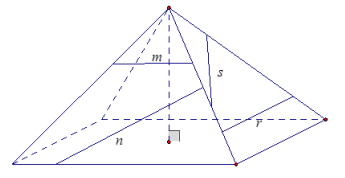
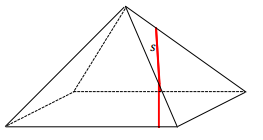
a. For segments n, s, and r, sketch the resulting slice from slicing the right rectangular pyramid with a slicing plane that contains the line segment and is perpendicular to the base.
b. For segment m, sketch the resulting slice from slicing the right rectangular pyramid with a slicing plane that contains the segment and is parallel to the base.
Note: To challenge yourself, you can try drawing the slice into the pyramid.
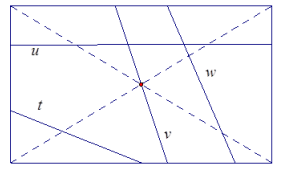
c. A top view of a right rectangular pyramid is given. The line segments lie in the base face. For each line segment, sketch the slice that results from slicing the right rectangular pyramid with a plane that contains the line segment and is perpendicular to the base.
Answer:
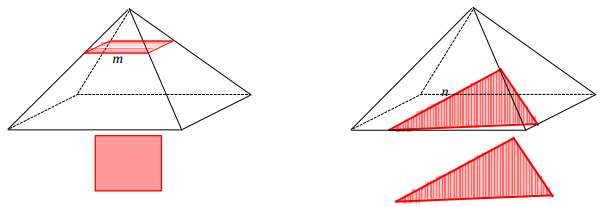
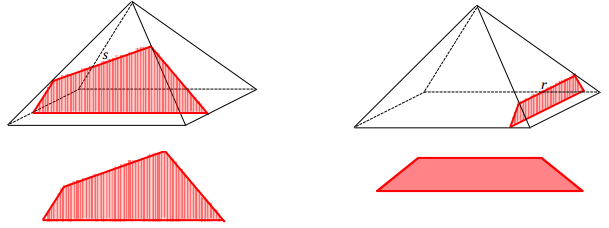
Note that the diagram for the slice made through s is from a perspective different from the one in the original pyramid. From the original perspective, the slice itself would not be visible and would appear as follows:
c. 
Eureka Math Grade 7 Module 6 Lesson 17 Exit Ticket Answer Key
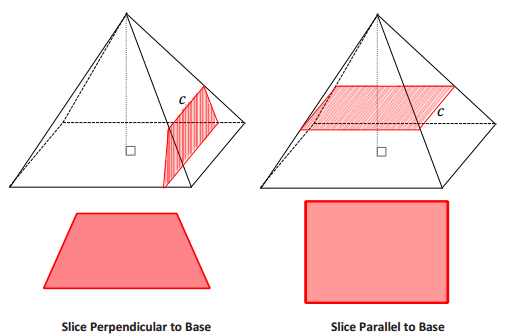
Question 1.
Two copies of the same right rectangular pyramid are shown below. Draw in the slice along segment c perpendicular to the base and the slice along segment c parallel to the base. Then, sketch the resulting slices as two-dimensional figures.
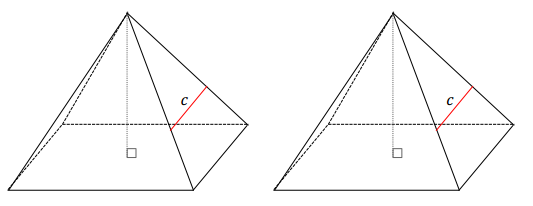
Slice Perpendicular to Base Slice Parallel to Base
Answer: