Engage NY Eureka Math 7th Grade Module 6 Lesson 12 Answer Key
Eureka Math Grade 7 Module 6 Lesson 12 Exploratory Challenge Answer Key
Question 1.
Use your tools to draw △ABC in the space below, provided AB = 5 cm, BC = 3 cm, and ∠A = 30°. Continue with the rest of the problem as you work on your drawing.
a. What is the relationship between the given parts of △ABC?
b. Which parts of the triangle can be drawn without difficulty? What makes this drawing challenging?
c. A ruler and compass are instrumental in determining where C is located.
✓ Even though the length of segment AC is unknown, extend the ray AC in anticipation of the intersection with segment BC.
✓ Draw segment BC with length 3 cm away from the drawing of the triangle.
✓ Adjust your compass to the length of \(\overline{B C}\).
✓ Draw a circle with center B and a radius equal to BC, or 3 cm.
d. How many intersections does the circle make with segment AC? What does each intersection signify?
e. Complete the drawing of △ABC.
f. Did the results of your drawing differ from your prediction?
Answer:
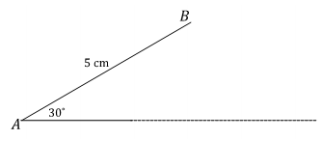
a. Two sides and a non-included angle are provided.
b. The parts that are adjacent, \(\overline{A B}\) and ∠A, are easiest to draw. It is difficult to position \(\overline{B C}\).
c. 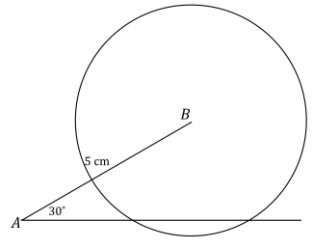
d. Two intersections; each intersection represents a possible location for vertex C.
e. 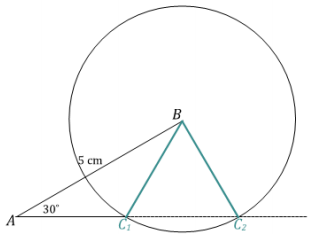
f. Answers will vary.
Question 2.
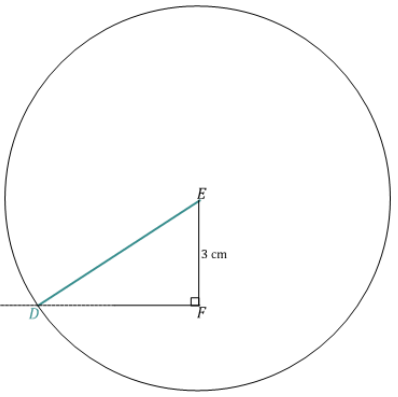
Now attempt to draw △DEF in the space below, provided DE = 5 cm, EF = 3 cm, and ∠F = 90°. Continue with the rest of the problem as you work on your drawing.
a. How are these conditions different from those in Exercise 1, and do you think the criteria will determine a unique triangle?
b. What is the relationship between the given parts of △DEF?
c. Describe how you will determine the position of \(\overline{D E}\).
d. How many intersections does the circle make with \(\overline{F D}\)?
e. Complete the drawing of △DEF. How is the outcome of △DEF different from that of △ABC?
f. Did your results differ from your prediction?
Answer:
a. The provided angle was an acute angle in Exercise 1; now the provided angle is a right angle. Possible prediction: Since the same general criteria (two sides and a non-included angle) determined more than one triangle in Exercise 1, the same can happen in this situation.

b. Two sides and a non-included angle are provided.
c. I will draw a segment equal in length to \(\overline{D E}\), or 5 cm, and adjust my compass to this length. Then, I will draw a circle with center E and radius equal to DE. This circle should intersect with the ray FD.
d. Just one intersection.
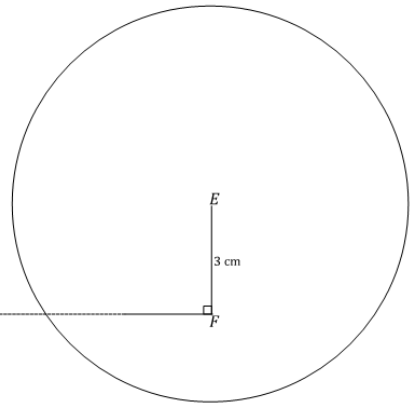
e. In drawing △ABC, there are two possible locations for vertex C, but in drawing △DEF, there is only one location for vertex D.
f. Answers will vary.
Question 3.
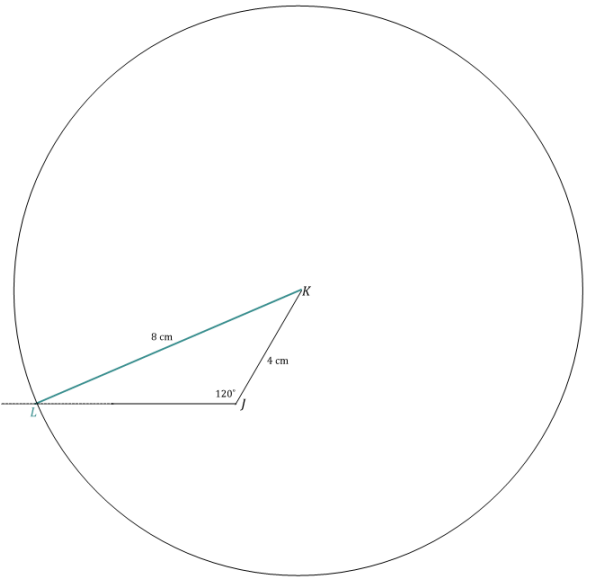
Now attempt to draw △JKL, provided KL = 8 cm, KJ = 4 cm, and ∠J = 120°. Use what you drew in Exercises 1 and 2 to complete the full drawing.
Answer:
Question 4.
Review the conditions provided for each of the three triangles in the Exploratory Challenge, and discuss the uniqueness of the resulting drawing in each case.
Answer:
All three triangles are under the condition of two sides and a non-included angle. The non-included angle in △ABC is an acute angle, while the non-included angle in △DEF is 90°, and the non-included angle in △JKL is obtuse. The triangles drawn in the latter two cases are unique because there is only one possible triangle that could be drawn for each. However, the triangle drawn in the first case is not unique because there are two possible triangles that could be drawn.
Eureka Math Grade 7 Module 6 Lesson 12 Problem Set Answer Key
Question 1.
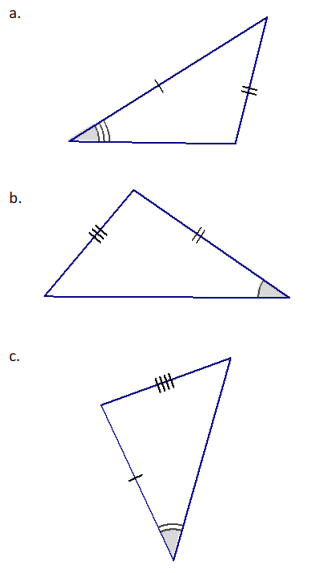
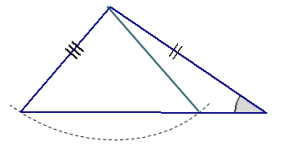
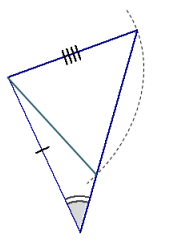
In each of the triangles below, two sides and a non-included acute angle are marked. Use a compass to draw a nonidentical triangle that has the same measurements as the marked angle and marked sides (look at Exercise 1,
part (e) of the Exploratory Challenge as a reference). Draw the new triangle on top of the old triangle. What is true about the marked angles in each triangle that results in two non-identical triangles under this condition?
Answer:
a. The non-included angle is acute.
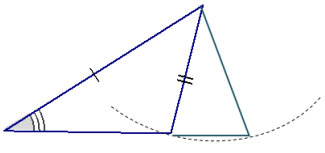
b. The non-included angle is acute.
c. The non-included angle is acute.
Question 2.
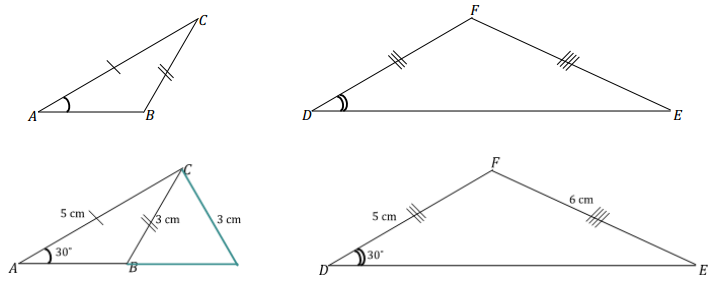
Sometimes two sides and a non-included angle of a triangle determine a unique triangle, even if the angle is acute. In the following two triangles, copy the marked information (i.e., two sides and a non-included acute angle), and discover which determines a unique triangle. Measure and label the marked parts.
In each triangle, how does the length of the marked side adjacent to the marked angle compare with the length of the side opposite the marked angle? Based on your drawings, specifically state when the two sides and acute non-included angle condition determines a unique triangle.

Answer:
While redrawing △ABC, students will see that a unique triangle is not determined, but in redrawing △DEF, a unique triangle is determined. In △ABC, the length of the side opposite the angle is shorter than the side adjacent to the angle. However, in △DEF, the side opposite the angle is longer than the side adjacent to the angle.
The two sides and acute non-included angle condition determines a unique triangle if the side opposite the angle is longer than the side adjacent to the angle.
Question 3.
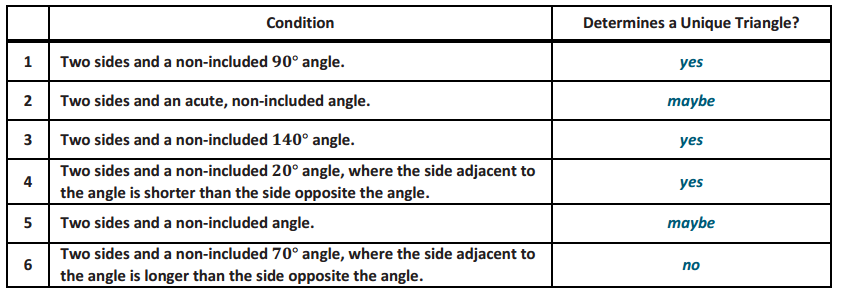
A sub-condition of the two sides and non-included angle is provided in each row of the following table. Decide whether the information determines a unique triangle. Answer with a yes, no, or maybe (for a case that may or may not determine a unique triangle).
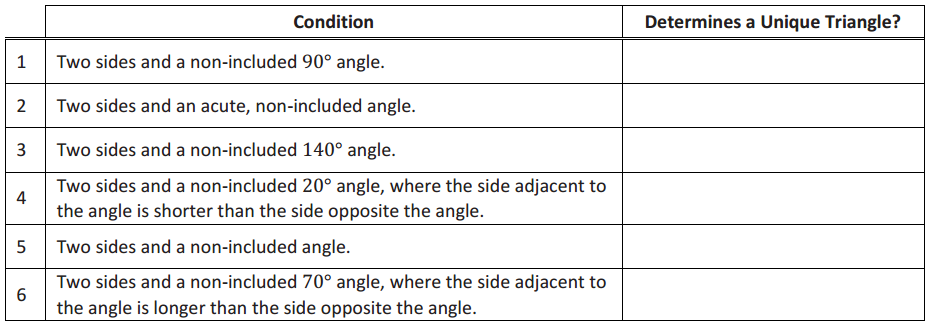
Answer:
Question 4.
Choose one condition from the table in Problem 3 that does not determine a unique triangle, and explain why.
Answer:
Possible response: Condition 6 does not determine a unique triangle because the condition of two sides and an acute non-included angle determines two possible triangles when the side adjacent to the angle is longer than the side opposite the angle.
Question 5.
Choose one condition from the table in Problem 3 that does determine a unique triangle, and explain why.
Answer:
Possible response: Condition 1 determines a unique triangle because the condition of two sides and a non-included angle with a measurement of 90° or more has a ray that only intersects the circle once.
Eureka Math Grade 7 Module 6 Lesson 12 Exit Ticket Answer Key
Question 1.
So far, we have learned about four conditions that determine unique triangles: three sides, two sides and an included angle, two angles and an included side, and two angles and the side opposite a given angle.
a. In this lesson, we studied the criterion two sides and a non-included angle. Which case of this criterion determines a unique triangle?
b. Provided \(\overline{A B}\) has length 5 cm, \(\overline{B C}\) has length 3 cm, and the measurement of ∠A is 30°, draw △ABC, and describe why these conditions do not determine a unique triangle.
Answer:
a. For the criterion two sides and a non-included angle, the case where the non-included angle is 90° or greater determines a unique triangle.
b. 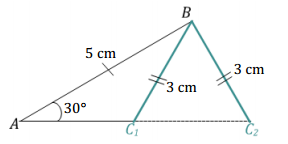
The non-included angle is an acute angle, and two different triangles can be determined in this case since \(\overline{B C}\) can be in two different positions, forming a triangle with two different lengths of \(\overline{A C}\).