Engage NY Eureka Math 7th Grade Module 6 Lesson 10 Answer Key
Eureka Math Grade 7 Module 6 Lesson 10 Exploratory Challenge Answer Key
Question 1.
A triangle XYZ has angle measures ∠X = 30° and ∠Y = 50° and included side XY = 6 cm. Draw △X’Y’Z’ under the same condition as △XYZ. Leave all construction marks as evidence of your work, and label all side and angle measurements.
Under what condition is △X’Y’Z’ drawn? Compare the triangle you drew to two of your peers’ triangles. Are the triangles identical? Did the condition determine a unique triangle? Use your construction to explain why.
Answer:
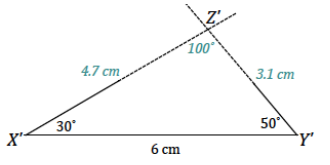
The condition on △X’Y’Z’ is the two angles and included side condition. All of the triangles are identical; the condition determined a unique triangle. After drawing the included side length, I used the protractor to draw the provided angle measurements at either endpoint of the included side \(\overline{X^{\prime} Y^{\prime}}\). Since these two angle measurements are fixed, the two remaining side lengths will intersect in one location, which is the third vertex of the triangle, Z’. There is no other way to draw this triangle; therefore, the condition determines a unique triangle.
Question 2.
A triangle RST has angle measures ∠S = 90° and ∠T = 45° and included side ST = 7 cm. Draw △R’S’T’ under the same condition. Leave all construction marks as evidence of your work, and label all side and angle measurements.
Under what condition is △R’S’T’ drawn? Compare the triangle you drew to two of your peers’ triangles. Are the triangles identical? Did the condition determine a unique triangle? Use your construction to explain why.
Answer:
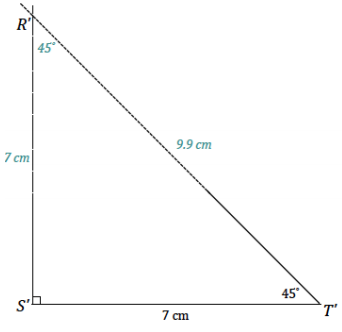
The condition on △R’ S’ T’ is the two angles and included side condition. All of the triangles are identical; the condition determined a unique triangle. After drawing the included side length, I used the protractor to draw the provided angle measurements at either endpoint of the included side \(\overline{S^{\prime} T^{\prime}}\). The intersection of the sides of the angle is the third vertex of the triangle, R’. There is no other way to draw this triangle; therefore, the condition determines a unique triangle.
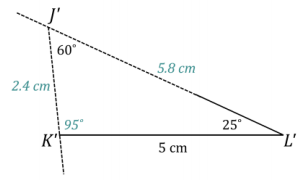
Question 3.
A triangle JKL has angle measures ∠J = 60° and ∠L = 25° and side KL = 5 cm. Draw △J’K’L’ under the same condition. Leave all construction marks as evidence of your work, and label all side and angle measurements.
Under what condition is △J’K’L’ drawn? Compare the triangle you drew to two of your peers’ triangles. Are the triangles identical? Did the condition determine a unique triangle? Use your construction to explain why.
Answer:
The condition on △J’K’L’ is the two angles and the side opposite a given angle condition. All of the triangles are identical; the condition determined a unique triangle. After drawing the given side length, I used the protractor to draw ∠L’ adjacent to \(\overline{K^{\prime} L^{\prime}}\). I drew the angle opposite the given side, ∠J’, on a slip of paper and lined up one ray of the angle on patty paper with one ray of the angle adjacent to the given side. I moved the angle on patty paper along the coinciding rays until the free ray just met the endpoint of \(\overline{K^{\prime} L^{\prime}}\). There is no other way to draw this triangle; therefore, the condition determines a unique triangle.
Question 4.
A triangle ABC has angle measures ∠C = 35° and ∠B = 105° and side AC = 7 cm. Draw △A’B’C’ under the same condition. Leave all construction marks as evidence of your work, and label all side and angle measurements.
Under what condition is △A’B’C’ drawn? Compare the triangle you drew to two of your peers’ triangles. Are the triangles identical? Did the condition determine a unique triangle? Use your construction to explain why.
Answer:
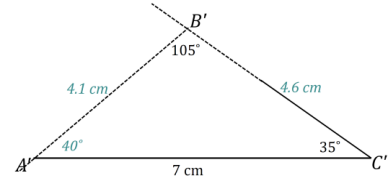
The condition on △A’B’C’ is the two angles and the side opposite a given angle condition. All of the triangles are identical; the condition determined a unique triangle. After drawing the given side length, I used the protractor to draw ∠C’ adjacent to \(\overline{A^{\prime} C^{\prime}}\). I drew the angle opposite the given side, ∠B’, on a slip of paper and lined up one ray of the angle on patty paper with one ray of the angle adjacent to the given side. I moved the angle on patty paper along the coinciding rays until the free ray just met the endpoint of \(\overline{A^{\prime} C^{\prime}}\). There is no other way to draw this triangle; therefore, the condition determines a unique triangle.
Eureka Math Grade 7 Module 6 Lesson 10 Problem Set Answer Key
Question 1.
In △FGH, ∠F = 42° and ∠H = 70°. FH = 6 cm. Draw △F’G’H’ under the same condition as △FGH. Leave all construction marks as evidence of your work, and label all side and angle measurements.
What can you conclude about △FGH and △F’G’H’? Justify your response.
Answer:
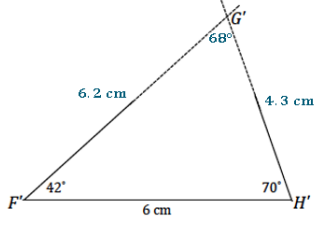
△FGH and △F’G’H’ are identical triangles by the two angles and included side condition. Since both triangles are drawn under the same condition, and the two angles and included side condition determines a unique triangle, both triangles determine the same unique triangle. Therefore, they are identical.
Question 2.
In △WXY, ∠Y = 57° and ∠W = 103°. Side YX = 6.5 cm. Draw △W’X’Y’ under the same condition as △WXY. Leave all construction marks as evidence of your work, and label all side and angle measurements.
What can you conclude about △WXY and △W’X’Y’? Justify your response.
Answer:
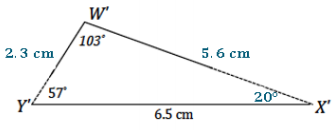
△WXY and △W’X’Y’ are identical triangles by the two angles and the side opposite a given angle condition. Since both triangles are drawn under the same condition, and the two angles and the side opposite a given angle condition determines a unique triangle, both triangles determine the same unique triangle. Therefore, they are identical.
Question 3.
Points A, Z, and E are collinear, and ∠B = ∠D. What can be concluded about △ABZ and △EDZ? Justify your answer.
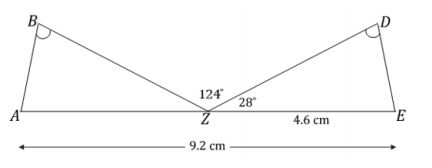
Answer:
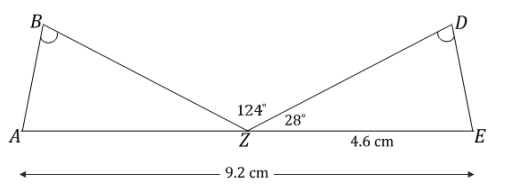
△ABZ and △EDZ are identical by the two angles and the side opposite a given angle condition. Since segments add, and AE is 9.2 cm and ZE is 4.6 cm, AZ must be 4.6 cm. Since angles on a line sum to 180°, ∠BZD = 124°,
and ∠DZE = 28°, then ∠AZB = 28°. From the diagram, we can see that ∠B = ∠D. The same measurements in both triangles satisfy the two angles and the side opposite a given angle condition, which means they both determine the same unique triangle; thus, they are identical.
Question 4.
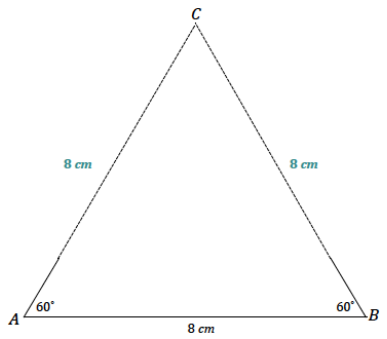
Draw △ABC so that ∠A has a measurement of 60°, ∠B has a measurement of 60°, and \(\overline{A B}\) has a length of 8 cm. What are the lengths of the other sides?
Answer:
Both of the other side lengths are 8 cm.
Question 5.
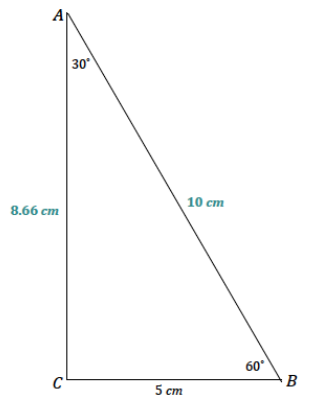
Draw △ABC so that ∠A has a measurement of 30°, ∠B has a measurement of 60°, and \(\overline{B C}\) has a length of 5 cm. What is the length of the longest side?
Answer:
The longest side has a length of 10 cm.
Eureka Math Grade 7 Module 6 Lesson 10 Exit Ticket Answer Key
Question 1.
△ABC has angle measures ∠A = 50° and ∠C = 90° and side AB = 5.5 cm. Draw △A’B’C’ under the same condition. Under what condition is △A’B’C’ drawn? Use your construction to explain why △A’B’C’ is or is not identical to △ABC.
Answer:
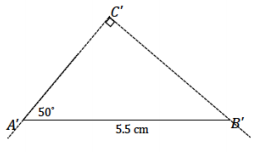
The condition on △A’B’C’ is the two angles and the side opposite a given angle condition. △A’B’C’ is identical to △ABC. After drawing the given side length, I used the protractor to draw ∠A’ adjacent to \(\overline{A^{\prime} B^{\prime}}\). I drew the angle opposite the given side, ∠B’, on a slip of paper and lined up one ray of the angle on patty paper with one ray of the angle adjacent to the given side. I moved the angle on patty paper along the coinciding rays until the free ray just met the endpoint of \(\overline{A^{\prime} B^{\prime}}\). There is no other way to draw this triangle; therefore, △A’B’C’ must be identical to △ABC.
Question 2.
△PQR has angle measures ∠Q = 25° and ∠R = 40° and included side QR = 6.5 cm. Draw △P’Q’R’ under the same condition. Under what condition is △P’Q’R’ drawn? Use your construction to explain why △P’Q’R’ is or is not identical to △PQR.
Answer:
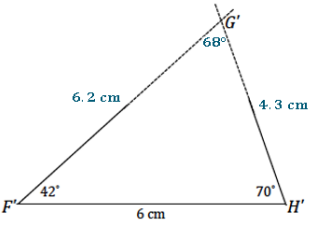
The condition on △P’Q’R’ is the two angles and included side condition. △P’Q’R’ is identical to △PQR. After drawing the given side length, I used the protractor to draw ∠Q’ adjacent to \(\overline{Q^{\prime} R^{\prime}}\). After drawing the included side length, I used the protractor to draw the provided angle measurements at either endpoint of the included side \(\overline{Q^{\prime} R^{\prime}}\). Since these two angle measurements are fixed, the two remaining side lengths will intersect in one location, which is the third vertex of the triangle, P’. There is no other way to draw this triangle; therefore,
△P’Q’R’ must be identical to △PQR.