Engage NY Eureka Math 7th Grade Module 3 Lesson 15 Answer Key
Eureka Math Grade 7 Module 3 Lesson 15 Example Answer Key
Example
A local car dealership is trying to sell all of the cars that are on the lot. Currently, there are 525 cars on the lot, and the general manager estimates that they will consistently sell 50 cars per week. Estimate how many weeks it will take for the number of cars on the lot to be less than 75.
Write an inequality that can be used to find the number of full weeks, w, it will take for the number of cars to be less than 75. Since w is the number of full or complete weeks, w = 1 means at the end of week 1.
Answer:
525 – 50w < 75
Solve and graph the inequality.
Answer:
525 – 50w < 75
– 50w + 525 – 525 < 75 – 525
– 50w + 0 < – 450 ( – \(\frac{1}{50}\))( – 50w) > ( – \(\frac{1}{50}\))( – 450)
w > 9
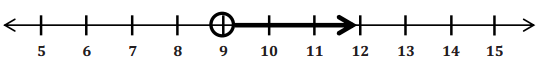
Interpret the solution in the context of the problem.
Answer:
The dealership can sell 50 cars per week for more than 9 weeks to have less than 75 cars remaining on the lot.
Verify the solution.
Answer:
w = 9:
525 – 50w < 75
525 – 50(9) < 75
525 – 450 < 75
75 < 75
False
w = 10:
525 – 50w < 75
525 – 50(10) < 75
525 – 500 < 75
25 < 75
True
Eureka Math Grade 7 Module 3 Lesson 15 Exercise Answer Key
Exercise 1.
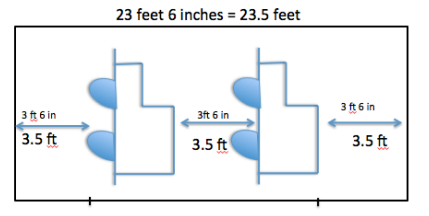
Two identical cars need to fit into a small garage. The opening is 23 feet 6 inches wide, and there must be at least 3 feet 6 inches of clearance between the cars and between the edges of the garage. How wide can the cars be?
Answer:
Encourage students to begin by drawing a diagram to illustrate the problem. A sample diagram is as follows:
Have students try to find all of the widths that the cars could be. Challenge them to name one more width than the person next to them. While they name the widths, plot the widths on a number line at the front of the class to demonstrate the shading. Before plotting the widths, ask if the circle should be open or closed as a quick review of graphing inequalities. Ultimately, the graph should be

→ Describe how to find the width of each car.
To find the width of each car, I subtract the minimum amount of space needed on either side of each car and in between the cars from the total length. Altogether, the amount of space needed was 3(3.5 ft.) or 10.5 ft. Then, I divided the result, 23.5 – 10.5 = 13, by 2 since there were 2 cars. The answer would be no more than \(\frac{13}{2}\) ft. or 6.5 ft.
→ Did you take an algebraic approach to finding the width of each car or an arithmetic approach? Explain.
Answers will vary.
→ If arithmetic was used, ask, “If w is the width of one car, write an inequality that can be used to find all possible values of w.”
2w + 10.5 ≤ 23.5
→ Why is an inequality used instead of an equation?
Since the minimum amount of space between the cars and each side of the garage is at least 3 feet 6 inches, which equals 3.5 ft., the space could be larger than 3 feet 6 inches. If so, then the width of the cars would be smaller. Since the width in between the cars and on the sides is not exactly 3 feet 6 inches, and it could be more, then there are many possible car widths. An inequality will give all possible car widths.
→ If an algebraic approach was used initially, ask, “How is the work shown in solving the inequality similar to the arithmetic approach?”
The steps to solving the inequality are the same as in an arithmetic approach. First, determine the total minimum amount of space needed by multiplying 3 by 3.5. Then, subtract 10.5 from the total of 23.5 and divide by 2.
→ What happens if the width of each car is less than 6.5 feet?
The amount of space between the cars and on either side of the car and garage is more then 3 feet 6 inches.
→ What happens if the width of each car is exactly 6.5 feet?
The amount of space between the cars and on either side of the car and garage is exactly 3 feet 6 inches.
→ What happens if the width of each car is more than 6.5 feet?
The amount of space between the cars and on either side of the car and garage is less than 3 feet 6 inches.
→ How many possible car widths are there?
Any infinite number of possible widths.
→ What assumption is being made?
The assumption made is that the width of the car is greater than 0 feet. The graph illustrates all possible values less than 6.5 feet, but in the context of the problem, we know that the width of the car must be greater than 0 feet.
→ Since we have determined there is an infinite amount, how can we illustrate this on a number line?
Illustrate by drawing a graph with a closed circle on 6.5 and an arrow drawn to the left.
→ What if 6.5 feet could not be a width, but all other possible measures less than 6.5 can be a possible width; how would the graph be different?
The graph would have an open circle on 6.5 and an arrow drawn to the left.
Exercise 2.
The cost of renting a car is $25 per day plus a one – time fee of $75.50 for insurance. How many days can the car be rented if the total cost is to be no more than $525?
a. Write an inequality to model the situation.
Answer:
Let x represent the number of days the car is rented.
25x + 75.50 ≤ 525
b. Solve and graph the inequality.
Answer:
25x + 75.50 ≤ 525
25x + 75.50 – 75.50 ≤ 525 – 75.50
25x + 0 ≤ 449.50
(\(\frac{1}{25}\)(25x) ≤ (\(\frac{1}{25}\))(449.50)
x ≤ 17.98
OR
25x + 75.50 ≤ 525
2,500x + 7,550 ≤ 52,500
2,500x + 7,550 – 7,550 ≤ 52,500 – 7,550
(\(\frac{1}{2,500}\))(2,500x) ≤ (\(\frac{1}{2,500}\))(44,950)
x ≤ 17.98
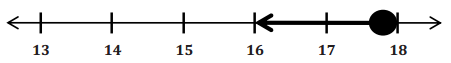
c. Interpret the solution in the context of the problem.
Answer:
The car can be rented for 17 days or fewer and stay within the amount of $525. The number of days is an integer. The 18th day would put the cost over $525, and since the fee is charged per day, the solution set includes whole numbers.
Exercise 3.
Mrs. Smith decides to buy three sweaters and a pair of jeans. She has $120 in her wallet. If the price of the jeans is $35, what is the highest possible price of a sweater, if each sweater is the same price?
Answer:
Let w represent the price of one sweater.
3w + 35 ≤ 120
3w + 35 – 35 ≤ 120 – 35
3w + 0 ≤ 85
(\(\frac{1}{3}\))(3w) ≤ (\(\frac{1}{3}\))(85)
w ≤ 28.33
Graph:

Solution: The highest price Mrs. Smith can pay for a sweater and have enough money is $28.33.
Exercise 4.
The members of the Select Chorus agree to buy at least 250 tickets for an outside concert. They buy 20 fewer lawn tickets than balcony tickets. What is the least number of balcony tickets bought?
Answer:
Let b represent the number of balcony tickets.
Then b – 20 represents the number of lawn tickets.
b + b – 20 ≥ 250
2b – 20 ≥ 250
2b – 20 + 20 ≥ 250 + 20
2b + 0 ≥ 270
(\(\frac{1}{2}\))(2b) ≥ (\(\frac{1}{2}\))(270)
b ≥ 135
Graph:
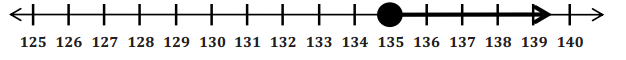
Solution: The least number of balcony tickets bought is 135. The answers need to be integers.
Exercise 5.
Samuel needs $29 to download some songs and movies on his MP3 player. His mother agrees to pay him $6 an hour for raking leaves in addition to his $5 weekly allowance. What is the minimum number of hours Samuel must work in one week to have enough money to purchase the songs and movies?
Answer:
Let h represent the number of hours Samuel rakes leaves.
6h + 5 ≥ 29
6h + 5 – 5 ≥ 29 – 5
6h + 0 ≥ 24
(\(\frac{1}{6}\))(6h) ≥ (\(\frac{1}{6}\))(24)
h ≥ 4
Graph:
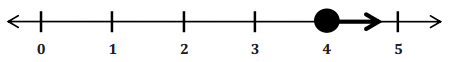
Solution: Samuel needs to rake leaves at least 4 hours to earn $29. Any amount of time over 4 hours will earn him extra money.
Eureka Math Grade 7 Module 3 Lesson 15 Problem Set Answer Key
Question 1.
Ben has agreed to play fewer video games and spend more time studying. He has agreed to play less than 10 hours of video games each week. On Monday through Thursday, he plays video games for a total of 5 \(\frac{1}{2}\) hours. For the remaining 3 days, he plays video games for the same amount of time each day. Find t, the amount of time he plays video games for each of the 3 days. Graph your solution.
Answer:
Let t represent the time in hours spent playing video games.
3t + 5 \(\frac{1}{2}\) < 10
3t + 5 \(\frac{1}{2}\) – 5 \(\frac{1}{2}\) < 10 – 5 \(\frac{1}{2}\)
3t + 0 < 4 \(\frac{1}{2}\)
(\(\frac{1}{3}\))(3t) < (\(\frac{1}{3}\))(4 \(\frac{1}{2}\))
t < 1.5
Graph:

Ben plays less than 1.5 hours of video games each of the three days.
Question 2.
Gary’s contract states that he must work more than 20 hours per week. The graph below represents the number of hours he can work in a week.

a. Write an algebraic inequality that represents the number of hours, h, Gary can work in a week.
Answer:
h > 20
b. Gary is paid $15.50 per hour in addition to a weekly salary of $50. This week he wants to earn more than $400. Write an inequality to represent this situation.
Answer:
15.50h + 50 > 400
c. Solve and graph the solution from part (b). Round your answer to the nearest hour.
Answer:
15.50h + 50 – 50 > 400 – 50
15.50h > 350
(\(\frac{1}{15.50}\))(15.50h) > 350(\(\frac{1}{15.50}\))
h > 22.58
Gary has to work 23 or more hours to earn more than $400.
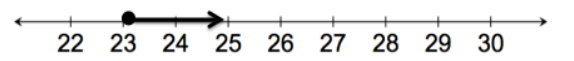
Question 3.
Sally’s bank account has $650 in it. Every week, Sally withdraws $50 to pay for her dog sitter. What is the maximum number of weeks that Sally can withdraw the money so there is at least $75 remaining in the account? Write and solve an inequality to find the solution, and graph the solution on a number line.
Answer:
Let w represent the number of weeks Sally can withdraw the money.
650 – 50w ≥ 75
650 – 50w – 650 ≥ 75 – 650
– 50w ≥ – 575
(\(\frac{1}{ – 50}\))( – 50w) ≥ (\(\frac{1}{ – 50}\))( – 575)
w ≤ 11.5
The maximum number of weeks Sally can withdraw the weekly dog sitter fee is 11 weeks.

Question 4.
On a cruise ship, there are two options for an Internet connection. The first option is a fee of $5 plus an additional $0.25 per minute. The second option costs $50 for an unlimited number of minutes. For how many minutes, m, is the first option cheaper than the second option? Graph the solution.
Answer:
Let m represent the number of minutes of Internet connection.
5 + 0.25m < 50
5 + 0.25m – 5 < 50 – 5
0.25m + 0 < 45
(\(\frac{1}{0.25}\))(0.25m) < (\(\frac{1}{0.25}\))(45)
m < 180
If there are less than 180 minutes, or 3 hours, used on the Internet, then the first option would be cheaper. If 180 minutes or more are planned, then the second option is more economical.

Question 5.
The length of a rectangle is 100 centimeters, and its perimeter is greater than 400 centimeters. Henry writes an inequality and graphs the solution below to find the width of the rectangle. Is he correct? If yes, write and solve the inequality to represent the problem and graph. If no, explain the error(s) Henry made.

Answer:
Henry’s graph is incorrect. The inequality should be 2(100) + 2w > 400. When you solve the inequality, you get w > 100. The circle on 100 on the number line is correct; however, the circle should be an open circle since the perimeter is not equal to 400. Also, the arrow should be pointing in the opposite direction because the perimeter is greater than 400, which means the width is greater than 100. The given graph indicates an inequality of less than or equal to.
Eureka Math Grade 7 Module 3 Lesson 15 Exit Ticket Answer Key
Question 1.
The junior high art club sells candles for a fundraiser. The first week of the fundraiser, the club sells 7 cases of candles. Each case contains 40 candles. The goal is to sell at least 13 cases. During the second week of the fundraiser, the club meets its goal. Write, solve, and graph an inequality that can be used to find the possible number of candles sold the second week.
Answer:
Let n represent the number candles sold the second week.
\(\frac{n}{40}\) + 7 ≥ 13
\(\frac{n}{40}\) + 7 – 7 ≥ 13 – 7
\(\frac{n}{40}\) ≥ 6
(40)(\(\frac{n}{40}\)) ≥ 6(40)
n ≥ 240
The minimum number of candles sold the second week was 240.

OR
Let n represent the number of cases of candles sold the second week.
40n + 280 ≥ 520
40n + 280 – 280 ≥ 520 – 280
40n + 0 ≥ 240
(\(\frac{1}{40}\))(40n) ≥ 240(\(\frac{1}{40}\))
n ≥ 6

The minimum number of cases sold the second week was 6. Since there are 40 candles in each case, the minimum number of candles sold the second week would be (40)(6) = 240.
Eureka Math Grade 7 Module 3 Lesson 15 Inequalities Answer Key
Progression of Exercises
Determine the value(s) of the variable.
Set 1
Question 1.
x + 1 > 8
Answer:
x > 7
Question 2.
x + 3 > 8
Answer:
x > 5
Question 3.
x + 10 > 8
Answer:
x > – 2
Question 4.
x – 2 > 3
Answer:
x > 5
Question 5.
x – 4 > 3
Answer:
x > 7
Set 2
Question 1.
3x ≤ 15
Answer:
x ≤ 5
Question 2.
3x ≤ 21
Answer:
x ≤ 7
Question 3.
– x ≤ 4
Answer:
x ≥ – 4
Question 4.
– 2x ≤ 4
Answer:
x ≥ – 2
Question 5.
– x ≤ – 4
Answer:
x ≥ 4
Set 3
Question 1.
\(\frac{1}{2}\) x < 1
Answer:
x < 2
Question 2.
\(\frac{1}{2}\)x < 3
Answer:
x < 6
Question 3.
– \(\frac{1}{5}\)x < 2 Answer: x > – 10
Question 4.
– \(\frac{2}{5}\) x < 2 Answer: x > – 5
Question 5.
– \(\frac{3}{5}\) x < 3 Answer: x > – 5
Set 4
Question 1.
2x + 4 ≥ 8
Answer:
x ≥ 2
Question 2.
2x – 3 ≥ 5
Answer:
x ≥ 4
Question 3.
– 2x + 1 ≥ 7
Answer:
x ≤ – 3
Question 4.
– 3x + 1 ≥ – 8
Answer:
x ≤ 3
Question 5.
– 3x – 5 ≥ 10
Answer:
x ≤ – 5
Set 5
Question 1.
2x – 0.5 > 5.5
Answer:
x > 3
Question 2.
3x + 1.5 > 4.5
Answer:
x > 2
Question 3.
5x – 3 > 4.5
Answer:
x > 1.5
Question 4.
– 5x + 2 > 8.5
Answer:
x < – 1.3 Question 5. – 9x – 3.5 > 1
Answer:
x < – 0.5
Set 6
Question 1.
2(x + 3) ≤ 4
Answer:
x ≤ – 1
Question 2.
3(x + 3) ≤ 6
Answer:
x ≤ – 1
Question 3.
4(x + 3) ≤ 8
Answer:
x ≤ – 1
Question 4.
– 5(x – 3) ≤ – 10
Answer:
x ≥ 5
Question 5.
– 2(x + 3) ≤ 8
Answer:
x ≥ – 7