Engage NY Eureka Math 7th Grade Module 3 Lesson 14 Answer Key
Eureka Math Grade 7 Module 3 Lesson 14 Example Answer Key
Example 1.
A youth summer camp has budgeted $2,000 for the campers to attend the carnival. The cost for each camper is $17.95, which includes general admission to the carnival and two meals. The youth summer camp must also pay $250 for the chaperones to attend the carnival and $350 for transportation to and from the carnival. What is the greatest number of campers who can attend the carnival if the camp must stay within its budgeted amount?
Answer:
Let c represent the number of campers to attend the carnival.
17.95c + 250 + 350 ≤ 2000
17.95c + 600 ≤ 2000
17.95c + 600 – 600 ≤ 2000 – 600
17.95c ≤ 1400
(\(\frac{1}{17.95}\))(17.95c) ≤ (\(\frac{1}{17.95}\))(1400)
c ≤ 77.99
In order for the camp to stay in budget, the greatest number of campers who can attend the carnival is 77 campers.
Example 2.
The carnival owner pays the owner of an exotic animal exhibit $650 for the entire time the exhibit is displayed. The owner of the exhibit has no other expenses except for a daily insurance cost. If the owner of the animal exhibit wants to make more than $500 in profits for the 5 \(\frac{1}{2}\) days, what is the greatest daily insurance rate he can afford to pay?
Answer:
Let i represent the daily insurance cost.
650 – 5.5i > 500
– 5.5i + 650 – 650 > 500 – 650
– 5.5i + 0> – 150
(\(\frac{1}{ – 5.5}\))( – 5.5i)>(\(\frac{1}{ – 5.5}\))( – 150)
i<27.27 The maximum daily cost the owner can pay for insurance is $27.27. Example 3. Several vendors at the carnival sell products and advertise their businesses. Shane works for a recreational company that sells ATVs, dirt bikes, snowmobiles, and motorcycles. His boss paid him $500 for working all of the days at the carnival plus 5% commission on all of the sales made at the carnival. What was the minimum amount of sales Shane needed to make if he earned more than $1,500? Answer: Let s represent the sales, in dollars, made during the carnival. 500 + \(\frac{5}{100}\) s > 1,500
\(\frac{5}{100}\) s + 500 > 1,500
\(\frac{5}{100}\) s + 500 – 500 > 1,500 – 500
\(\frac{5}{100}\) s + 0 > 1,000
(\(\frac{100}{5}\))(\(\frac{5}{100}\) s) > (\(\frac{100}{5}\))(1,000)
s > 20,000
The sales had to be more than $20,000 for Shane to earn more than $1,500.
Eureka Math Grade 7 Module 3 Lesson 14 Exercise Answer Key
Opening Exercise
The annual County Carnival is being held this summer and will last 5 \(\frac{1}{2}\) days. Use this information and the other given information to answer each problem.
You are the owner of the biggest and newest roller coaster called the Gentle Giant. The roller coaster costs $6 to ride. The operator of the ride must pay $200 per day for the ride rental and $65 per day for a safety inspection. If you want to make a profit of at least $1,000 each day, what is the minimum number of people that must ride the roller coaster?
Write an inequality that can be used to find the minimum number of people, p, which must ride the roller coaster each day to make the daily profit.
Answer:
6p – 200 – 65 ≥ 1000
Solve the inequality.
Answer:
6p – 200 – 65 ≥ 1000
6p – 265 ≥ 1000
6p – 265 + 265 ≥ 1000 + 265
6p + 0 ≥ 1265
(\(\frac{1}{6}\))(6p) ≥ (\(\frac{1}{6}\))(1265)
p ≥ 210 \(\frac{5}{6}\)
Interpret the solution.
Answer:
There needs to be a minimum of 211 people to ride the roller coaster every day to make a daily profit of at least $1,000.
Eureka Math Grade 7 Module 3 Lesson 14 Problem Set Answer Key
Question 1.
As a salesperson, Jonathan is paid $50 per week plus 3% of the total amount he sells. This week, he wants to earn at least $100. Write an inequality with integer coefficients for the total sales needed to earn at least $100, and describe what the solution represents.
Answer:
Let the variable p represent the purchase amount.
50 + \(\frac{3}{100}\) p ≥ 100
\(\frac{3}{100}\) p + 50 ≥ 100
(100)(\(\frac{3}{100}\) p) + 100(50) ≥ 100(100)
3p + 5000 ≥ 10000
3p + 5000 – 5000 ≥ 10000 – 5000
3p + 0 ≥ 5000
(\(\frac{1}{3}\))(3p) ≥ (\(\frac{1}{3}\))(5000)
p ≥ 1666 \(\frac{2}{3}\)
Jonathan must sell $1,666.67 in total purchases.
Question 2.
Systolic blood pressure is the higher number in a blood pressure reading. It is measured as the heart muscle contracts. Heather was with her grandfather when he had his blood pressure checked. The nurse told him that the upper limit of his systolic blood pressure is equal to half his age increased by 110.
a. a is the age in years, and p is the systolic blood pressure in millimeters of mercury (mmHg). Write an inequality to represent this situation.
Answer:
p ≤ \(\frac{1}{2}\) a + 110
b. Heather’s grandfather is 76 years old. What is normal for his systolic blood pressure?
Answer:
p ≤ \(\frac{1}{2}\) a + 110, where a = 76.
p ≤ \(\frac{1}{2}\) (76) + 110
p ≤ 38 + 110
p ≤ 148
A systolic blood pressure for his age is normal if it is at most 148 mmHG.
Question 3.
Traci collects donations for a dance marathon. One group of sponsors will donate a total of $6 for each hour she dances. Another group of sponsors will donate $75 no matter how long she dances. What number of hours, to the nearest minute, should Traci dance if she wants to raise at least $1,000?
Answer:
Let the variable h represent the number of hours Traci dances.
6h + 75 ≥ 1000
6h + 75 – 75 ≥ 1000 – 75
6h + 0 ≥ 925
(\(\frac{1}{6}\))(6h) ≥ (\(\frac{1}{6}\))(925)
h ≥ 154 \(\frac{1}{6}\)
Traci would have to dance at least 154 hours and 10 minutes.
Question 4.
Jack’s age is three years more than twice the age of his younger brother, Jimmy. If the sum of their ages is at most 18, find the greatest age that Jimmy could be.
Answer:
Let the variable j represent Jimmy’s age in years.
Then, the expression 3 + 2j represents Jack’s age in years.
j + 3 + 2j ≤ 18
3j + 3 ≤ 18
3j + 3 – 3 ≤ 18 – 3
3j ≤ 15
(\(\frac{1}{3}\))(3j) ≤ (\(\frac{1}{3}\))(15)
j ≤ 5
Jimmy’s age is 5 years or less.
Question 5.
Brenda has $500 in her bank account. Every week she withdraws $40 for miscellaneous expenses. How many weeks can she withdraw the money if she wants to maintain a balance of a least $200?
Answer:
Let the variable w represent the number of weeks.
500 – 40w ≥ 200
500 – 500 – 40w ≥ 200 – 500
– 40w ≥ – 300
( – \(\frac{1}{40}\))( – 40w) ≤ ( – \(\frac{1}{40}\))( – 300)
w ≤ 7.5
$40 can be withdrawn from the account for seven weeks if she wants to maintain a balance of at least $200.
Question 6.
A scooter travels 10 miles per hour faster than an electric bicycle. The scooter traveled for 3 hours, and the bicycle traveled for 5 \(\frac{1}{2}\) hours. Altogether, the scooter and bicycle traveled no more than 285 miles. Find the maximum speed of each.
Answer:
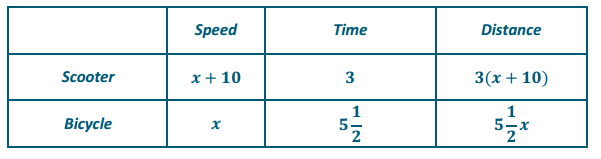
3(x + 10) + 5 \(\frac{1}{2}\) x ≤ 285
3x + 30 + 5 \(\frac{1}{2}\) x ≤ 285
8 \(\frac{1}{2}\) x + 30 ≤ 285
8 \(\frac{1}{2}\) x + 30 – 30 ≤ 285 – 30
8 \(\frac{1}{2}\) x ≤ 255
\(\frac{17}{2}\) x ≤ 255
(\(\frac{2}{17}\))(\(\frac{17}{2}\) x) ≤ (255)(\(\frac{2}{17}\))
x ≤ 30
The maximum speed the bicycle traveled was 30 miles per hour, and the maximum speed the scooter traveled was 40 miles per hour.
Eureka Math Grade 7 Module 3 Lesson 14 Exit Ticket Answer Key
Question 1.
Games at the carnival cost $3 each. The prizes awarded to winners cost $145.65. How many games must be played to make at least $50?
Answer:
Let g represent the number of games played.
3g – 145.65 ≥ 50
3g – 145.65 + 145.65 ≥ 50 + 145.65
3g + 0 ≥ 195.65
(\(\frac{1}{3}\))(3g) ≥ (\(\frac{1}{3}\))(195.65)
g ≥ 65.217
There must be at least 66 games played to make at least $50.