Engage NY Eureka Math 7th Grade Module 1 Lesson 16 Answer Key
Eureka Math Grade 7 Module 1 Lesson 16 Opening Exercise Answer Key
Opening Exercise: Can You Guess the Image?
Question 1.
This is a reduction of a subway map.
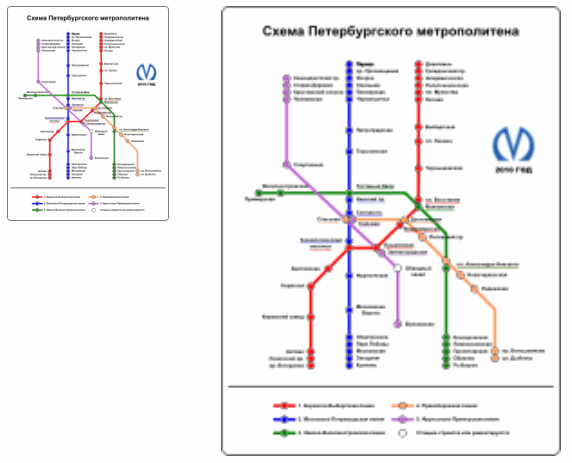
Question 2.

Answer:

Eureka Math Grade 7 Module 1 Lesson 16 Example Answer Key
Example 1.
For the following problems, (a) is the actual picture, and (b) is the scale drawing. Is the scale drawing an enlargement or a reduction of the actual picture?
Question 1.

Answer:

Question 2.
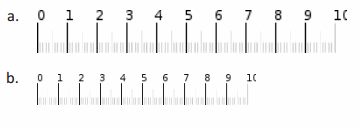
Answer:
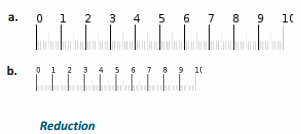
SCALE DRAWING: A reduced or enlarged two-dimensional drawing of an original two-dimensional drawing.
Example 2.
Derek’s family took a day trip to a modern public garden. Derek looked at his map of the park that was a reduction of the map located at the garden entrance. The dots represent the placement of rare plants. The diagram below is the top-view as Derek held his map while looking at the posted map.
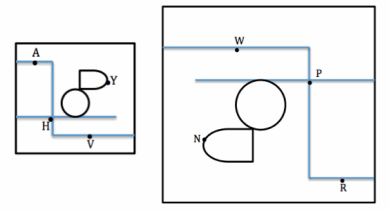
What are the corresponding points of the scale drawings of the maps?
Point A to ___ Point V to ___ Point H to ___ Point Y to ___
Answer:
Point A to Point R Point V to Point W Point H to Point P Point Y to Point N
Eureka Math Grade 7 Module 1 Lesson 16 Exploratory Challenge Answer Key
Create scale drawings of your own modern nesting robots using the grids provided.
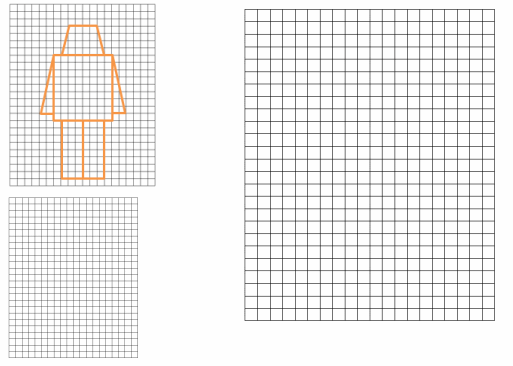
Answer:
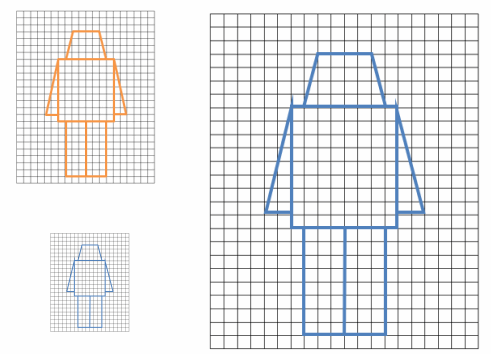
Example 3.
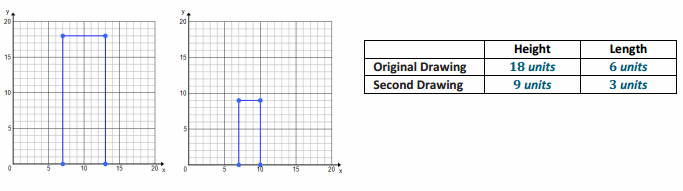
Celeste drew an outline of a building for a diagram she was making and then drew a second one mimicking her original drawing. State the coordinates of the vertices and fill in the table.
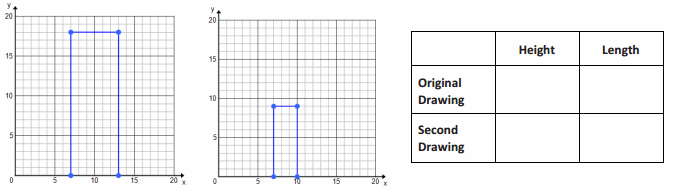
Notes
Answer:
Eureka Math Grade 7 Module 1 Lesson 16 Exercise Answer Key
Exercise
Luca drew and cut out a small right triangle for a mosaic piece he was creating for art class. His mother liked the mosaic piece and asked if he could create a larger one for their living room. Luca made a second template for his triangle pieces.
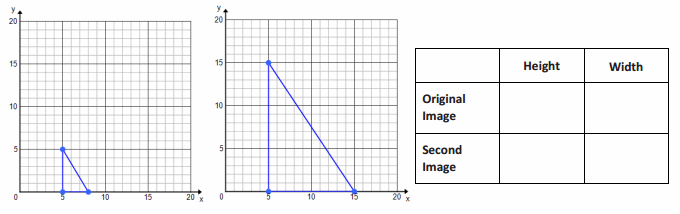
Answer:
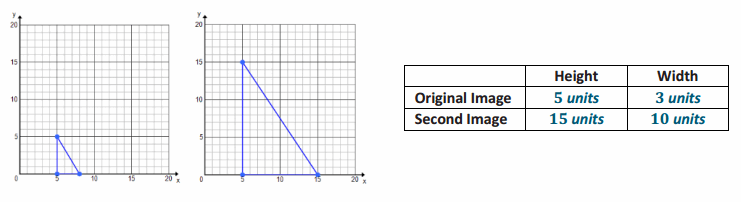
a. Does a constant of proportionality exist? If so, what is it? If not, explain.
Answer:
No, because the ratios of corresponding side lengths are not equal or proportional to each other.
b. Is Luca’s enlarged mosaic a scale drawing of the first image? Explain why or why not.
Answer:
No, the enlarged mosaic image is not a scale drawing of the first image. We know this because the images do not have all side lengths proportional to each other; there is no constant of proportionality.
Eureka Math Grade 7 Module 1 Lesson 16 Exit Ticket Answer Key
Use the following figure on the graph for Problems 1 and 2.
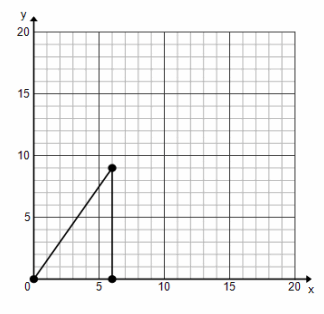
Question 1.
a. If the original lengths are multiplied by 2, what are the new coordinates?
Answer:
(0,0), (12,18), (12,0)
b. Use the table to organize lengths (the vertical and horizontal legs).

Answer:

c. Is the new drawing a reduction or an enlargement?
Answer:
Enlargement
d. What is the constant of proportionality?
Answer:
2
Question 2.
a. If the original lengths are multiplied by \(\frac{1}{3}\) , what are the new coordinates?
Answer:
(0,0), (2,3), (2,0)
b. Use the table to organize lengths (the vertical and horizontal legs).

Answer:

c. Is the new drawing a reduction or an enlargement?
Answer:
Reduction
d. What is the constant of proportionality?
Answer:
\(\frac{1}{3}\)
Eureka Math Grade 7 Module 1 Lesson 16 Problem Set Answer Key
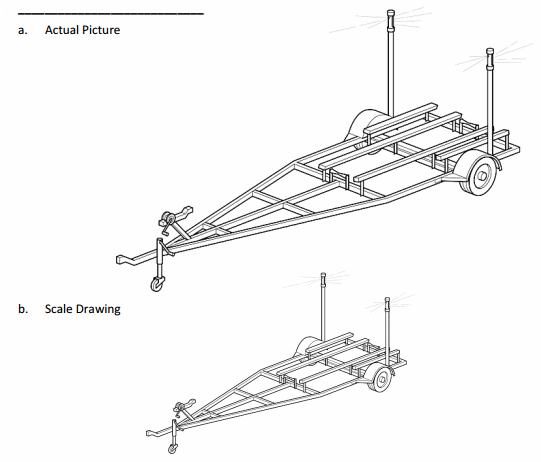
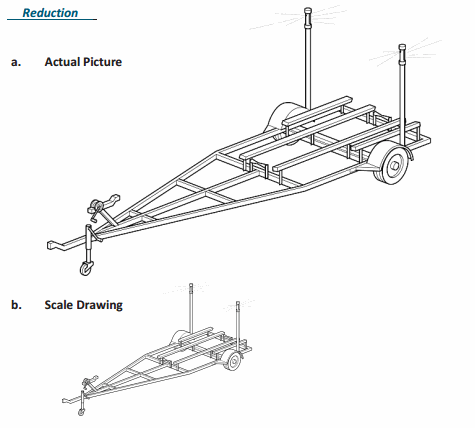
For Problems 1–3, identify if the scale drawing is a reduction or an enlargement of the actual picture.
Question 1.
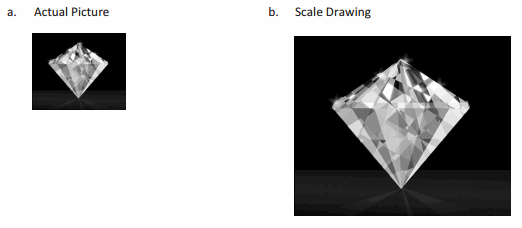
Answer:
Enlargement
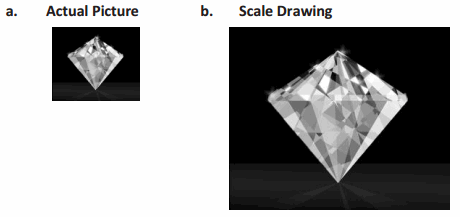
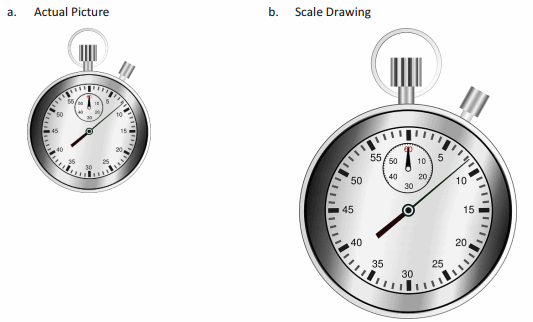
Question 2.
Answer:
Question 3.
Answer:
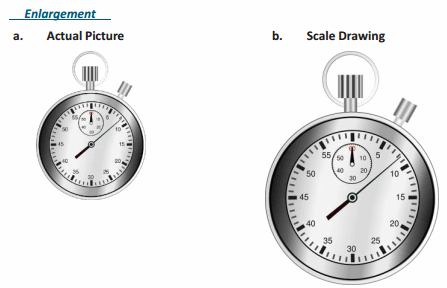
Question 4.
Using the grid and the abstract picture of a face, answer the following questions:
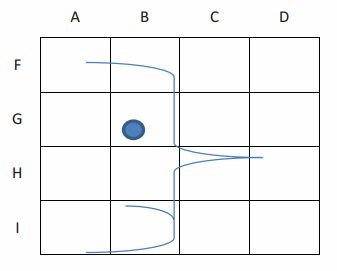
a. On the grid, where is the eye?
Answer:
Intersection BG
b. What is located in DH?
Answer:
Tip of the nose
c. In what part of the square BI is the chin located?
Answer:
Bottom right corner
Question 5.
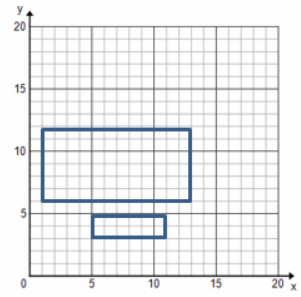
Use the blank graph provided to plot the points and decide if the rectangular cakes are scale drawings of each other.
Cake 1: (5, 3), (5, 5), (11, 3), (11, 5)
Cake 2: (1, 6), (1, 12), (13, 12), (13, 6)
How do you know?
Answer:
These images are not scale drawings of each other because the short length of Cake 2 is three times longer than Cake 1, but the longer length of Cake 2 is only twice as long as Cake 1. Both should either be twice as long or three times as long to have one-to-one correspondence and to be scale drawings of each other.