Engage NY Eureka Math 7th Grade Module 1 Lesson 18 Answer Key
Eureka Math Grade 7 Module 1 Lesson 18 Example Answer Key
Example 1.
Basketball at Recess?
Vincent proposes an idea to the Student Government to install a basketball hoop along with a court marked with all the shooting lines and boundary lines at his school for students to use at recess. He presents a plan to install a half-court design as shown below. After checking with the school administration, he is told it will be approved if it fits on the empty lot that measures 25 feet by 75 feet on the school property. Will the lot be big enough for the court he planned? Explain.
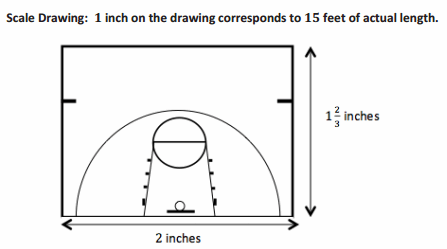
Answer:

Scale Factor: 1 inch corresponds to (15∙12) inches, or 180 inches, so the scale factor is 180. Let k = 180, x represent the scale drawing lengths in inches, and y represent the actual court lengths in inches. The y-values must be converted from feet to inches.
To find actual length: y = 180x
y = 180(2)
y = 360 inches, or 30 feet
To find actual width: y = 180x
y = 180(1 \(\frac{2}{3}\))
y = \(\frac{180}{1}\)∙\(\frac{5}{3}\)
y = 300 inches, or 25 feet
The actual court measures 25 feet by 30 feet. Yes, the lot is big enough for the court Vincent planned. The court will take up the entire width of the lot.
Example 2
The diagram shown represents a garden. The scale is 1 centimeter for every 20 meters. Each square in the drawing measures 1 cm by 1 cm. Find the actual length and width of the garden based upon the given drawing.
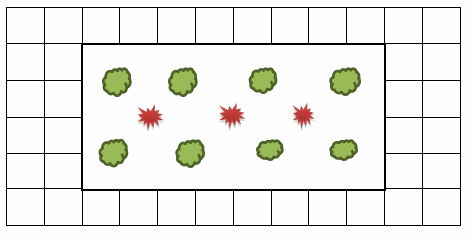
Answer:
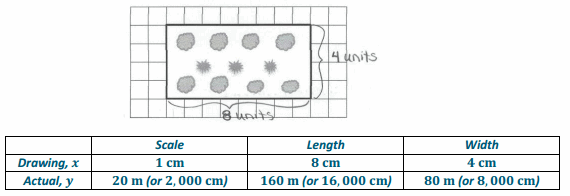
Method 1:
Using the given scale: 1 cm of scale drawing length corresponds to 20 m of actual length.
k = 0 Drawing length to actual length
To find the actual length: y = 20x Where x represents the the scale drawing measurements in centimeters, and y represents the actual measurement in meters.
y = 20(8) Substitute the scale drawing length in place of x.
y = 160
The actual length is 80 m.
To find actual width: Divide the actual length by 2 since its drawing width is half the length.
The actual width is 80 m.
Method 2:
Use the scale factor: 1 cm of scale drawing length corresponds to 2000 cm of actual length.
k = 2000 Drawing length to actual length (in same units)
To find actual length: y = 2000x Where x represents the drawing measurement in centimeters, and
y represents the actual measurement in centimeters.
y = 2000(8) Substitute the scale drawing length in place of x.
y = 16000
The actual length is 16,000 cm, or 160 m.
To find actual width: y = 2000x
y = 2000(4) Substitute the scale drawing width in place of x.
y = 8000
Example 3
A graphic designer is creating an advertisement for a tablet. She needs to enlarge the picture given here so that 0.25 inches on the scale picture corresponds to 1 inch on the actual advertisement. What will be the length and width of the tablet on the advertisement?
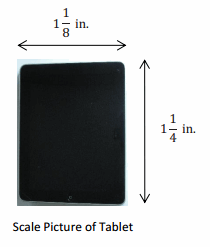
Answer:
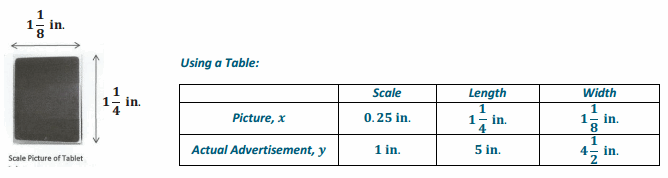
Using an Equation:
Find the constant of proportionality, k: k = 4
k = 4 (Scale factor since units of measure are the same; it is an enlargement.)
To find Actual Length: y = 4x Where x represents the picture measurement, and y represents the
actual advertisement measurement.
y = 4(1 \(\frac{1}{4}\)) Substitute the picture length in place of x.
y = 5
To find Actual Width: y = 4x
y = 4(1\(\frac{1}{8}\)) Substitute the picture width in place of y.
y = 4\(\frac{1}{2}\)
The tablet will be 5 inches by 4\(\frac{1}{2}\) inches on the actual advertisement.
Eureka Math Grade 7 Module 1 Lesson 18 Exercise Answer Key
Students from the high school are going to perform one of the acts from their upcoming musical at the atrium in the mall. The students want to bring some of the set with them so that the audience can get a better feel for the whole production. The backdrop that they want to bring has panels that measure 10 feet by 10 feet. The students are not sure if they will be able to fit these panels through the entrance of the mall since the panels need to be transported flat (horizontal). They obtain a copy of the mall floor plan, shown below, from the city planning office. Use this diagram to decide if the panels will fit through the entrance. Use a ruler to measure.
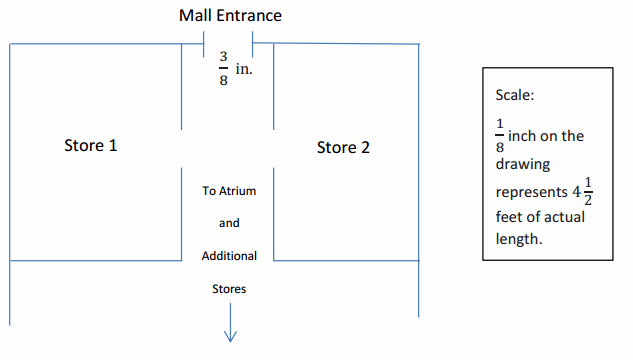
Answer the following questions.
a. Find the actual distance of the mall entrance, and determine whether the set panels will fit.
Answer:
Step 1: Relationship between lengths in drawing and lengths in actual
Scale: ![]() or the value of the ratio \(\frac{36}{1}\) feet to inches
or the value of the ratio \(\frac{36}{1}\) feet to inches
Scale factor calculations: ![]() inches to inches
inches to inches
![]()
= 432, an enlargement
Step 2: Find the actual distance of the entrance.
Using the given scale: \(\frac{3}{8}\)∙\(\frac{36}{1}\) = 13\(\frac{1}{2}\)
The actual distance of the entrance is 13 \(\frac{1}{2}\) feet wide.
OR
Using the scale factor: \(\frac{3}{8}\)∙\(\frac{432}{1}\) = 162
The actual distance of the entrance is 162 inches, or 13\(\frac{1}{2}\) feet, wide.
Yes, the set panels, which are 10 ft. ×10 ft. , will fit (lying flat) through the mall entrance.
b. What is the scale factor? What does it tell us?
Answer:
The scale factor is 432. Each length on the scale drawing is \(\frac{1}{432}\) of the actual length. The actual lengths are 432 times larger than the lengths in the scale drawing.
Eureka Math Grade 7 Module 1 Lesson 18 Problem Set Answer Key
Question 1.
A toy company is redesigning its packaging for model cars. The graphic design team needs to take the old image shown below and resize it so that \(\frac{1}{2}\) inch on the old packaging represents \(\frac{1}{3}\) inch on the new package. Find the length of the image on the new package.

Answer:
\(\frac{4}{3}\) inches; the scale \(\frac{1}{2}\) to \(\frac{1}{3}\) and the length of the original figure is 2, which is 4 halves, so in the scale drawing the length will be 4 thirds.
Question 2.
The city of St. Louis is creating a welcome sign on a billboard for visitors to see as they enter the city. The following picture needs to be enlarged so that \(\frac{1}{2}\) inch represents 7 feet on the actual billboard. Will it fit on a billboard that measures 14 feet in height?

Answer:
Yes, the drawing measures 1 inch in height, which corresponds to 14 feet on the actual billboard.
Question 3.
Your mom is repainting your younger brother’s room. She is going to project the image shown below onto his wall so that she can paint an enlarged version as a mural. Use a ruler to determine the length of the image of the train. Then determine how long the mural will be if the projector uses a scale where 1 inch of the image represents 2 \(\frac{1}{2}\) feet on the wall.

Answer:
The scale drawing measures 2 inches, so the image will measure 2 × 2.5, or 5 feet long, on the wall.
Question 4.
A model of a skyscraper is made so that 1 inch represents 75 feet. What is the height of the actual building if the height of the model is 18 \(\frac{3}{5}\) inches?
Answer:
1,395 feet
Question 5.
The portrait company that takes little league baseball team photos is offering an option where a portrait of your baseball pose can be enlarged to be used as a wall decal (sticker). Your height in the portrait measures 3 \(\frac{1}{2}\) inches. If the company uses a scale where 1 inch on the portrait represents 20 inches on the wall decal, find the height on the wall decal. Your actual height is 55 inches. If you stand next to the wall decal, will it be larger or smaller than you?
Answer:
Your height on the wall decal is 70 inches. The wall decal will be larger than your actual height (when you stand next to it).
Question 6.
The sponsor of a 5K run/walk for charity wishes to create a stamp of its billboard to commemorate the event. If the sponsor uses a scale where 1 inch represents 4 feet, and the billboard is a rectangle with a width of 14 feet and a length of 48 feet, what will be the shape and size of the stamp?
Answer:
The stamp will be a rectangle measuring 3 \(\frac{1}{2}\) inches by 12 inches.
Question 7.
Danielle is creating a scale drawing of her room. The rectangular room measures 20 \(\frac{1}{2}\) ft. by 25 ft. If her drawing uses the scale where 1 inch represents 2 feet of the actual room, will her drawing fit on an 8 \(\frac{1}{2}\) in. by 11 in. piece of paper?
Answer:
No, the drawing would be 10\(\frac{1}{4}\) inches by 12 \(\frac{1}{2}\) inches, which is larger than the piece of paper.
Question 8.
A model of an apartment is shown below where \(\frac{1}{4}\) inch represents 4 feet in the actual apartment. Use a ruler to measure the drawing and find the actual length and width of the bedroom.
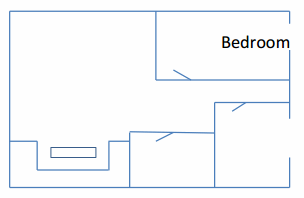
Answer:
Ruler measurements: 1\(\frac{1}{8}\) inches by \(\frac{9}{16}\) inches.
The actual length would be 18 feet, and the actual width would be 9 feet.
Eureka Math Grade 7 Module 1 Lesson 18 Exit Ticket Answer Key
A drawing of a surfboard in a catalog shows its length as 8\(\frac{4}{9}\) inches. Find the actual length of the surfboard if \(\frac{1}{2}\) inch length on the drawing corresponds to \(\frac{3}{8}\) foot of actual length.
Answer:

y = kx
y = \(\frac{3}{4}\) x
=8 \(\frac{4}{9}\) ∙\(\frac{3}{4}\)
= \(\frac{76}{9}\) ∙\(\frac{3}{4}\)
= \(\frac{19}{3}\) ∙\(\frac{1}{1}\)
The actual surfboard measures 6 \(\frac{1}{3}\) feet long.
Note: Students could also use an equation where y represents the scale drawing, and x represents the actual measurement, in which case, k would equal \(\frac{4}{3}\) .