Engage NY Eureka Math 6th Grade Module 3 Lesson 19 Answer Key
Eureka Math Grade 6 Module 3 Lesson 19 Exercise Answer Key
Exploratory Challenge
The Length of a Line Segment is the Distance Between its End Points
Exercise 1.
Locate and label (4, 5) and (4, – 3). Draw the line segment between the end points given on the coordinate plane. How long is the line segment that you drew? Explain.
Answer:
The length of the line segment is also 8 units. I found that the distance between (4, – 3) and (4, 5) is 8 units. Because the end points are on opposite sides of zero, I added the absolute values of the second coordinates together, so the distance from end to end is 8 units.
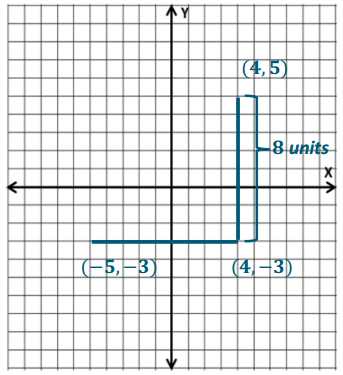
Exercise 2.
Draw a horizontal line segment starting at (4, – 3) that has a length of 9 units. What are the possible coordinates of the other end point of the line segment? (There is more than one answer.)
Answer:
(- 5, – 3) or (13, – 3)
Which point did you choose to be the other end point of the horizontal line segment? Explain how and why you chose that point. Locate and label the point on the coordinate grid.
Answer:
The other end point of the horizontal line segment is (- 5, – 3). I chose this point because the other option, (13, – 3), is located off of the given coordinate grid.
Note: Students may choose the end point (13, – 3), but they must change the number scale of the x-axis to do so.
Exercise 3.
Extending Lengths of Line Segments to Sides of Geometric Figures
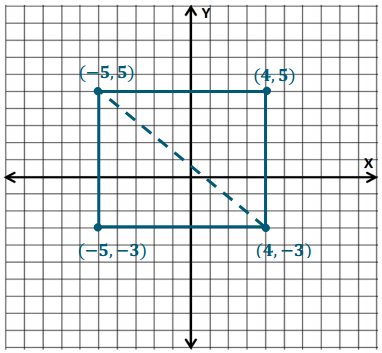
The two line segments that you have just drawn could be seen as two sides of a rectangle. Given this, the end points of the two line segments would be three of the vertices of this rectangle.
a. Find the coordinates of the fourth vertex of the rectangle. Explain how you find the coordinates of the fourth vertex using absolute value.
Answer:
The fourth vertex is (- 5, 5). The opposite sides of a rectangle are the same length, so the length of the vertical side starting at (- 5, – 3) has to be 8 units long. Also, the side from (- 5, – 3) to the remaining vertex is a vertical line, so the end points must have the same first coordinate. |- 3| = 3, and 8 – 3 = 5, so the remaining vertex must be five units above the x-axis.
Note: Students can use a similar argument using the length of the horizontal side starting at (4, 5), knowing it has to be 9 units long.
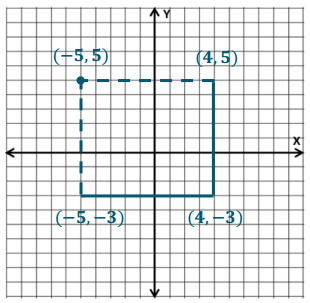
b. How does the fourth vertex that you found relate to each of the consecutive vertices in either direction?
Explain.
The fourth vertex has the same first coordinate as (- 5, – 3) because they are the end points of a vertical line segment. The fourth vertex has the same second coordinate as (4, 5) since they are the end points of a horizontal line segment.
c. Draw the remaining sides of the rectangle.
Answer:
Using Lengths of Sides of Geometric Figures to Solve Problems
Exercise 4.
Using the vertices that you have found and the lengths of the line segments between them, find the perimeter of the rectangle.
Answer:
8 + 9 + 8 + 9 = 34; the perimeter of the rectangle is 34 units.
Exercise 5.
Find the area of the rectangle.
Answer:
9 × 8 = 72; the area of the rectangle is 72 units2.
Exercise 6.
Draw a diagonal line segment through the rectangle with opposite vertices for end points. What geometric figures are formed by this line segment? What are the areas of each of these figures? Explain.
Answer:
The diagonal line segment cuts the rectangle into two right triangles. The areas of the triangles are 36 units2 each because the triangles each make up half of the rectangle, and half of 72 is 36.
Extension (If time allows): Line the edge of a piece of paper up to the diagonal in the rectangle. Mark the length of the diagonal on the edge of the paper. Align your marks horizontally or vertically on the grid, and estimate the length of the diagonal to the nearest integer. Use that estimation to now estimate the perimeter of the triangles.
Answer:
The length of the diagonal is approximately 12 units, and the perimeter of each triangle is approximately 29 units.
Exercise 7
Construct a rectangle on the coordinate plane that satisfies each of the criteria listed below. Identify the coordinate of each of its vertices.
→ Each of the vertices lies in a different quadrant.
→ Its sides are either vertical or horizontal.
→ The perimeter of the rectangle is 28 units.
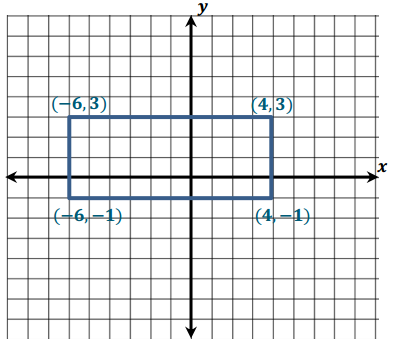
Answers will vary. The example to the right shows a rectangle with side lengths 10 and 4 units. The coordinates of the rectangle’s vertices are (- 6,3), (4, 3), (4, – 1), and (- 6, – 1).
Using absolute value, show how the lengths of the sides of your rectangle provide a perimeter of 28 units.
Answer:
|- 6| = 6, |4| = 4, and 6 + 4 = 10, so the width of my rectangle is 10 units.
|3| = 3, |-1| = 1, and 3 + 1 = 4, so the height of my rectangle is 4 units.
10 + 4 + 10 + 4 = 28, so the perimeter of my rectangle is 28 units.
Eureka Math Grade 6 Module 3 Lesson 19 Problem Set Answer Key
Question 1.
One end point of a line segment is (-3, -6). The length of the line segment is 7 units. Find four points that could serve as the other end point of the given line segment.
Answer:
(- 10, – 6); (4, – 6); (- 3, 1); (- 3, – 13)
Question 2.
Two of the vertices of a rectangle are (1, – 6) and (- 8, – 6). If the rectangle has a perimeter of 26 units, what are the coordinates of its other two vertices?
Answer:
(1, – 2) and (- 8, – 2), or (1, – 10) and (- 8, – 10)
Question 3.
A rectangle has a perimeter of 28 units, an area of 48 square units, and sides that are either horizontal or vertical. If one vertex is the point (- 5, – 7) and the origin is In the interior of the rectangle, find the vertex of the rectangle that is opposite (- 5, – 7).
Answer:
(1, 1)
Eureka Math Grade 6 Module 3 Lesson 19 Exit Ticket Answer Key
Question 1.
The coordinates of one end point of a line segment are (- 2, – 7). The line segment is 12 units long. Give three
possible coordinates of the line segment’s other end point.
Answer:
(10, – 7); (- 14, – 7); (- 2, 5); (- 2, – 19)
Question 2.
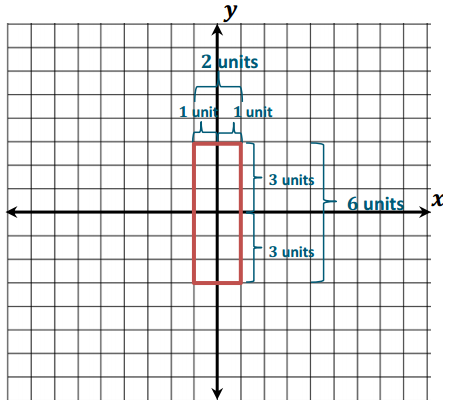
Graph a rectangle with an area of 12 units2 such that its vertices lie in at least two of the four quadrants in the coordinate plane. State the lengths of each of the sides, and use absolute value to show how you determined the lengths of the sides.
Answer:
Answers will vary. The rectangle can have side lengths of 6 and 2 or 3 and 4. A sample is provided on the grid on the right. 6 × 2 = 12
Eureka Math Grade 6 Module 3 Lesson 19 Opening Exercise Answer Key
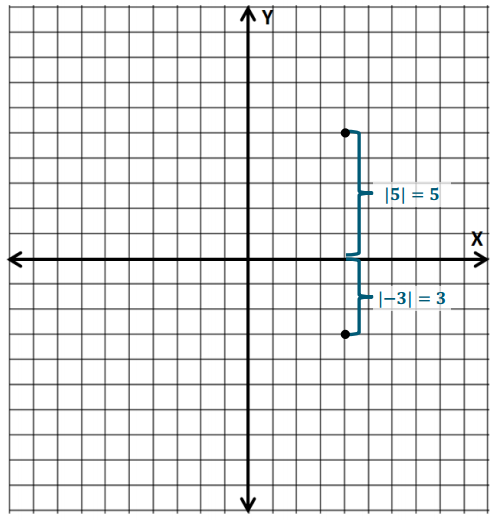
Question 1.
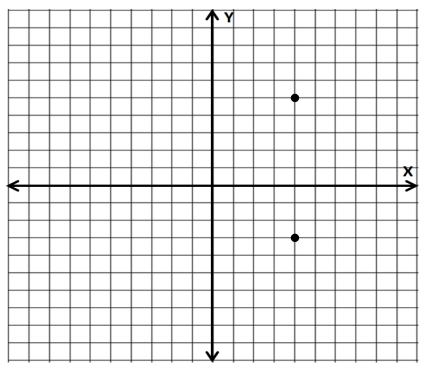
In the coordinate plane, find the distance between the points using absolute value.
Answer:
The distance between the points is 8 units. The points have the same first coordinates and, therefore, lie on the same vertical line. |- 3| = 3, and |5| = 5, and the numbers lie on opposite sides of 0, so their absolute values are added together; 3 + 5 = 8. We can check our answer by just counting the number of units between the two points.