Engage NY Eureka Math Grade 6 Module 5 Lesson 17 Answer Key
Eureka Math Grade 6 Module 5 Lesson 17 Opening Exercise Answer Key
Opening Exercise:
a. Write a numerical equation for the area of the figure below. Explain and identify different parts of the figure.
i. 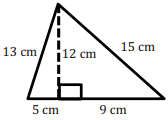
Answer:
A = \(\frac{1}{2}\) (14 cm)(12 cm) = 84cm2
14 cm represents the bose of the figure because 5 cm + 9 cm = 14 cm, and 12 cm represents the altitude of the figure because it forms a right angle with the base.
ii. How would you write an equation that shows the area of a triangle with base b and height h?
Answer:
A = \(\frac{1}{2}\) bh
b. Write a numerical equation for the area of the figure below. Explain and identify different parts of the figure.
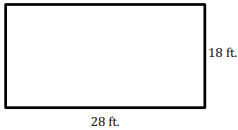
Answer:
A = (28 ft.)(18 ft) = 504 ft2
28 ft. represents the base of the rectangle, 18 ft. and 18 ft. represents the height of the rectangle.
ii. How would you write an equation that shows the area of a rectangle with base b and height h?
Answer:
A = bh.
Eureka Math Grade 6 Module 5 Lesson 17 Example Answer Key
Example 1:
Use the net to calculate the surface area of the figure. (Note: all measurements are in centimeters.)
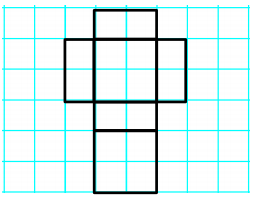
Answer:
→ When you are calculating the area of a figure, what are you finding?
The area of a figure is the amount of space inside a two-dimensional figure.
→ The surface area is similar to the area, but the surface area is used to describe three-dimensional figures. What do you think is meant by the surface area of a solid?
The surface area of a three-dimensional figure is the area of each face added together.
→ What type of figure does the net create? How do you know?
It creates a rectangular prism because there are six rectangular faces.
If the boxes on the grid paper represent a 1 cm × 1 cm box, label the dimensions of the net.
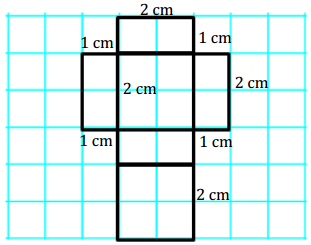
→ The surface area of a figure is the sum of the areas of all faces. Calculate the area of each face, and record this value inside the corresponding rectangle.
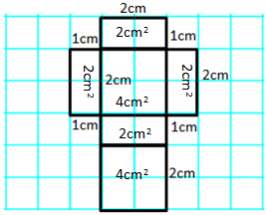
→ In order to calculate the surface area, we have to find the sum of the areas we calculated since they represent the area of each face. There are two faces that have an area of 4 cm2 and four faces that have an area of 2 cm2. How can we use these areas to write a numerical expression to show how to calculate the surface area of the net?
The numerical expression to calculate the surface area of the net would be
(1 cm × 2 cm) + (1 cm × 2 cm) + (1 cm × 2 cm) + (1 cm × 2 cm) + (2 cm × 2 cm)+ (2 cm × 2 cm).
→ Write the expression more compactly, and explain what each part represents on the net.
4(1 cm × 2 cm) + 2(2 cm × 2 cm)
The expression means there are 4 rectangles that have dimensions 1 cm × 2 cm on the net and 2 rectangles that have dimensions 2 cm × 2 cm on the net.
→ What is the surface area of the net?
The surface area of the net is 16 cm2.
Example 2:
Use the net to write an expression for surface area. (Note: all measurements are in square feet.)
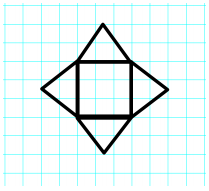
Answer:
→ What type of figure does the net create? How do you know?
It creates a square pyramid because one face is a square and the other four faces are triangles.
→ If the boxes on the grid paper represent a 1 ft. × 1 ft. square, label the dimensions of the net.
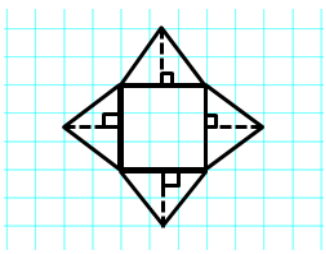
→ How many faces does the rectangular pyramid have?
5
→ Knowing the figure has 5 faces, use the knowledge you gained in Example ito calculate the surface area of the rectangular pyramid.
Area of Base: 3 ft. × 3 ft. = 9 ft2
Area of Triangles: \(\frac{1}{2}\) × 3 ft. × 2 ft. = 3 ft2
Surface Area: 9 ft2 + 3 ft2 + 3 ft2 + 3 ft2 + 3 ft2 = 21 ft2
Eureka Math Grade 6 Module 5 Lesson 17 Exercise Answer Key
Exercises:
Name the solid the net would create, and then write an expression for the surface area. Use the expression to determine the surface area. Assume that each box on the grid paper represents a 1 cm × 1 cm square. Explain how the expression represents the figure.
Exercise 1.
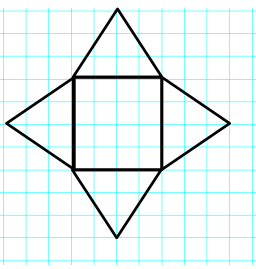
Answer:
Name of Shape: Rectangular Pyramid, but more specifically a Square Pyramid
Surface Area: 4 cm × 4 cm + 4(\(\frac{1}{2}\) × 4 cm × 3 cm)
Work: 16 cm2 + 4(6 cm2) = 40 cm2
The surface area is 40 cm2. The figure is made up of a square base that measures 4 cm × 4 cm and four triangles, each with a base of 4 cm and a height of 3 cm.
Exercise 2.
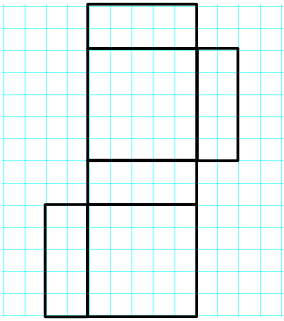
Answer:
Name of Shape: Rectangular Prism
Surface Area: 2(5 cm × 5 cm) + 4(5 cm × 2 cm)
Work: 2(25 cm2 ) + 4(10 cm2) = 90 cm2
The surface area is 90 cm2. The figure has 2 square faces, each of which measures 5 cm × 5 cm, and 4 rectangular faces, each of which measures 5 cm × 2 cm.
Exercise 3.
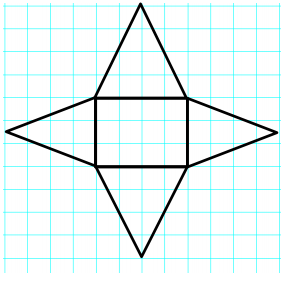
Answer:
Name of Shape: Rectangular Pyramid
SurfaceArea: 3 cm × 4 cm + 2(\(\frac{1}{2}\) × 4 cm × 4 cm)+ 2(\(\frac{1}{2}\) × 4 cm × 3 cm)
Work: 12 cm2 + 2(8 cm2) + 2(6 cm2) = 40 cm2
The surface area is 40 cm2. The figure has 1 rectangular base that measures 3 cm × 4 cm, 2 triangular faces, each with a bose of 4 cm and a height of 4 cm, and 2 other triangular faces, each with a base of 3 cm and a height of 4 cm.
Exercise 4.
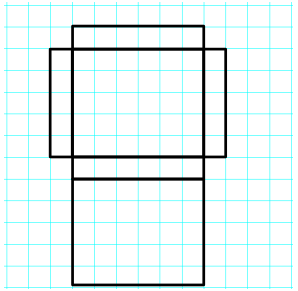
Answer:
Name of Shape: Rectangular Prism
Surface Area: 2(6 cm × 5 cm) + 2(5 cm × 1 cm) + 2(6 cm × 1 cm)
Work: 2(30 cm2) + 2(5 cm2) + 2(6 cm2) = 82 cm2
The surface area is 82 cm2. The figure has two 6 cm × 5 cm rectangular faces, two 5 cm × 1 cm rectangular faces, and two 6 cm × 1 cm rectangular faces.
Eureka Math Grade 6 Module 5 Lesson 17 Problem Set Answer Key
Name the shape, and write an expression for surface area. Calculate the surface area of the figure. Assume each box on the grid paper represents a 1 ft. × 1 ft. square.
Question 1.
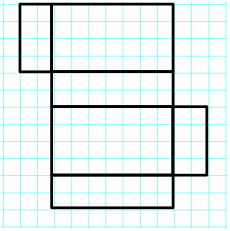
Answer:
Name of Shape: Rectangular Prism
SurfaceArea: (2 ft. × 4 ft.) + (2 ft. × 4 ft.)+ (4 ft. × 7 ft.) + (4 ft. × 7 ft.) + (7 ft. × 2 ft.)+ (7 ft. × 2 ft.)
Work: 2(2 ft. × 4 ft.) + 2(4 ft. × 7 ft.) + 2(7 ft. × 2 ft.)
= 16 ft2 + 56 ft2 + 28 ft2
= 100 ft2
Question 2.
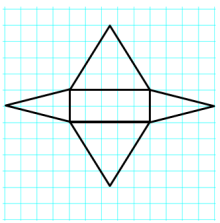
Answer:
Name of Shape: Rectangular Pyramid
SurfaceArea: (2 ft. × 5 ft.) + (\(\frac{1}{2}\) × 2ft. × 4ft.)+ (\(\frac{1}{2}\) × 2 ft. × 4ft.) + (\(\frac{1}{2}\) × 5 ft. × 4ft.) + \(\frac{1}{2}\) × 5ft. × 4 ft.)
Work: 2 ft. × 5 ft. + 2(\(\frac{1}{2}\) × 2 ft. × 4 ft.) + 2(\(\frac{1}{2}\) × 5 ft. × 4ft.)
= 10 ft2 + 8 ft2 + 20 ft2 = 38 ft2
Explain the error in each problem below. Assume each box on the grid paper represents a 1 m × 1 m square.
Question 3.
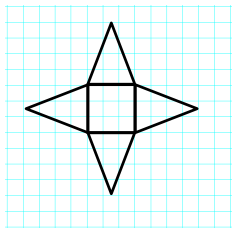
Name of Shape: Rectangular Pyramid, but more specifically a Square Pyramid
Area of Base: 3m × 3m = 9m2
Area of Triangles: 3 m × 4m = 12 m2
SurfaceArea: 9m2 + 12m2 + 12m2 + 12m2 + 12m2 = 57m2
Answer:
The error in the solution is the area of the triangles. In order to calculate the correct area of the triangles, you must use the correct formula A = \(\frac{1}{2}\)bh. Therefore, the area of each triangle would be 6 m2 and not 12 m2.
Question 4.
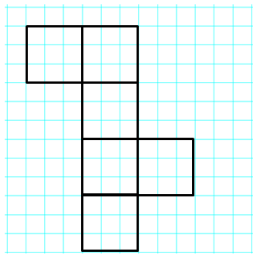
Name of Shape: Rectangular Prism or, more specifically. a Cube
Area of Faces: 3m × 3m = 9m2
Surface Area: 9 m2 + 9 m2 + 9 m2 + 9 m2 + 9 m2 = 45m2
Answer:
The surface area is incorrect because the student did not find the sum of all 6 faces. The solution is shown above only calculates the sum of 5 faces. Therefore, the correct surface area should be 9 m2 + 9 m2 + 9 m2 + 9 m2 + 9 m2 + 9m2 = 54m2 and not 45m2.
Question 5.
Sofia and Ella are both writing expressions to calculate the surface area of a rectangular prism. However, they wrote different expressions.
a. Examine the expressions below, and determine if they represent the same value. Explain why or why not. Sofia’s Expression:
(3 cm × 4 cm) + (3 cm × 4 cm) + (3 cm × 5 cm) + (3 cm × 5 cm) + (4 cm × 5 cm) + (4 cm × 5 cm)
Ella’s Expression:
2(3 cm × 4 cm) + 2(3 cm × 5 cm) + 2(4 cm × 5 cm)
Answer:
Sofia’s and Ella’s expressions are the same, but Ella used the distributive property to make her expression more compact than Sofia’s.
b. What fact about the surface area of a rectangular prism does Ella’s expression show more clearly than Sofia’s?
Answer:
A rectangular prism is composed of three pairs of sides with identical areas.
Eureka Math Grade 6 Module 5 Lesson 17 Exit Ticket Answer Key
Question 1.
Name the shape, and then calculate the surface area of the figure. Assume each box on the grid paper represents a 1 in. × 1 in. square.
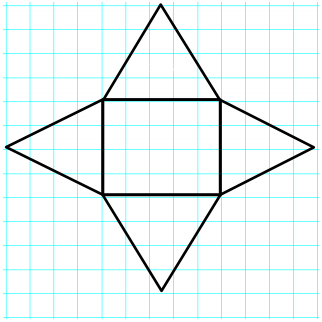
Answer:
Name of Shape: Rectangular Pyramid
Area of Base: 5 in. × 4 in. = 20 in2
Area of Triangles: \(\frac{1}{2}\) × 4 in. × 4 in. = 8 in2, \(\frac{1}{2}\) × 5 in. × 4 in. = 10 in2
SurfaceArea: 20 in2 +8 in2 + 8in2 + 10 in2 + 10 in2 = 56 in2
Eureka Math Grade 6 Module 5 Lesson 17 Addition and Subtraction Equations Answer Key
Addition and Subtraction Equations – Round 1:
Directions: Find the value of m in each equation.

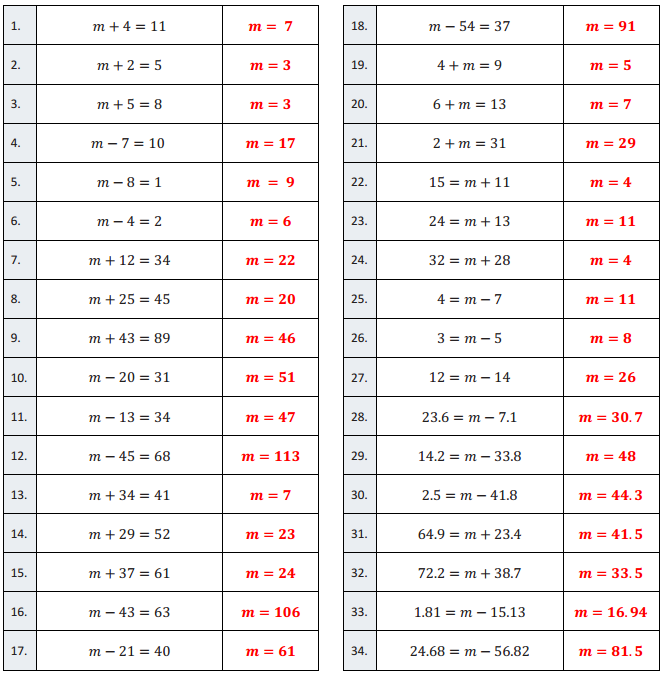
Question 1.
m + 4 = 11
Answer:
m = 7
Question 2.
m + 2 = 5
Answer:
m = 3
Question 3.
m + 5 = 8
Answer:
m = 3
Question 4.
m – 7 = 10
Answer:
m = 17
Question 5.
m – 8 = 1
Answer:
m = 9
Question 6.
m – 4 = 2
Answer:
m = 6
Question 7.
m + 12 = 34
Answer:
m = 22
Question 8.
m + 25 = 45
Answer:
m = 20
Question 9.
m + 43 = 89
Answer:
m = 46
Question 10.
m – 20 = 31
Answer:
m = 51
Question 11.
m – 13 = 34
Answer:
m = 47
Question 12.
m – 45 = 68
Answer:
m = 113
Question 13.
m + 34 = 41
Answer:
m = 7
Question 14.
m + 29 = 52
Answer:
m = 23
Question 15.
m + 37 = 61
Answer:
m = 24
Question 16.
m – 43 = 63
Answer:
m = 106
Question 17.
m – 21 = 40
valuem = 61
Question 18.
m – 54 = 37
Answer:
m = 91
Question 19.
4 + m = 9
Answer:
m = 5
Question 20.
6 + m = 13
Answer:
m = 7
Question 21.
2 + m = 31
Answer:
m = 29
Question 22.
15 = m + 11
Answer:
m = 4
Question 23.
24 = m + 13
Answer:
m = 11
Question 24.
32 = m + 28
Answer:
m = 4
Question 25.
4 = m – 7
Answer:
m = 11
Question 26.
3 = m – 5
Answer:
m = 8
Question 27.
12 = m – 14
Answer:
m = 26
Question 28.
23.6 = m – 7.1
Answer:
m = 30.7
Question 29.
14.2 = m – 33.8
Answer:
m = 48
Question 30.
2.5 = m -41.8
Answer:
m = 44.3
Question 31.
64.9 = m + 23.4
Answer:
m = 41.5
Question 32.
72.2 = m + 38.7
Answer:
m = 33.5
Question 33.
1.81 = m – 15.13
Answer:
m = 16.94
Question 34.
24.68 = m – 56.82
Answer:
m = 81.5
Addition and Subtraction Equations – Round 2:
Directions: Find the value of m in each equation.


Question 1.
m + 2 = 7
Answer:
m = 5
Question 2.
m + 4 = 10
Answer:
m = 6
Question 3.
m + 8 = 15
Answer:
m = 7
Question 4.
m + 7 = 23
Answer:
m = 16
Question 5.
m + 12 = 16
Answer:
m = 4
Question 6.
m – 5 = 2
Answer:
m = 7
Question 7.
m – 3 = 8
Answer:
m = 11
Question 8.
m – 4 = 12
Answer:
m = 16
Question 9.
m – 14 = 45
Answer:
m = 59
Question 10.
m + 23 = 40
Answer:
m = 17
Question 11.
m + 13 = 31
Answer:
m = 18
Question 12.
m – 23 = 48
Answer:
m = 25
Question 13.
m + 38 = 52
Answer:
m = 14
Question 14.
m – 14 = 27
Answer:
m = 41
Question 15.
m – 23 = 35
Answer:
m = 58
Question 16.
m – 17 = 18
Answer:
m = 35
Question 17.
m – 64 = 1
Answer:
m = 65
Question 18.
6 = m + 3
Answer:
m = 3
Question 19.
12 = m + 7
Answer:
m = 5
Question 20.
24 = m + 16
Answer:
m = 8
Question 21.
13 = m + 9
Answer:
m = 4
Question 22.
32 = m – 3
Answer:
m = 35
Question 23.
22 = m – 12
Answer:
m = 34
Question 24.
34 = m – 10
Answer:
m = 44
Question 25.
48 = m + 29
Answer:
m = 19
Question 26.
21 = m + 17
Answer:
m = 4
Question 27.
52 = m + 37
Answer:
m = 15
Question 28.
\(\frac{6}{7}\) + m = \(\frac{4}{7}\)
Answer:
m = \(\frac{2}{7}\)
Question 29.
\(\frac{2}{3}\) = m – \(\frac{5}{3}\)
Answer:
m = \(\frac{7}{3}\)
Question 30.
\(\frac{1}{4}\) – m = \(\frac{8}{3}\)
Answer:
m = \(\frac{35}{12}\)
Question 31.
\(\frac{5}{6}\) = m – \(\frac{7}{12}\)
Answer:
m = \(\frac{17}{12}\)
Question 32.
\(\frac{7}{8}\) = m – \(\frac{5}{12}\)
Answer:
m = \(\frac{31}{24}\)
Question 33.
\(\frac{7}{6}\) + m = \(\frac{16}{3}\)
Answer:
m = \(\frac{25}{6}\)
Question 34.
\(\frac{1}{3}\) + m = \(\frac{13}{15}\)
Answer:
m = \(\frac{8}{15}\)