Engage NY Eureka Math 6th Grade Module 3 Lesson 15 Answer Key
Eureka Math Grade 6 Module 3 Lesson 15 Example Answer Key
Example 1. Extending the Axes Beyond Zero
The point below represents zero on the number line. Draw a number line to the right starting at zero. Then, follow directions as provided by the teacher.
![]()
Answer:
→ Use a straightedge to extend the x-axis to the left of zero to represent the real number line horizontally, and complete the number line using the same scale as on the right side of zero.
→ Describe the y-axis. What types of numbers should it include?
The y-axis is a vertical number line that includes numbers on both sides of zero (above and below), and so it includes both positive and negative numbers.
→ Use a straightedge to draw a vertical number line above zero.
Provide students with time to draw.
→ Extend the y-axis below zero to represent the real number line vertically, and complete the number line using
the same scale as above zero.
Example 2: Components of the Coordinate Plane
All points on the coordinate plane are described with reference to the origin. What is the origin, and what are its coordinates?
Answer:
The origin is the point where the x- and y-axes intersect. The coordinates of the origin are (0, 0).
To describe locations of points in the coordinate plane, we use _________________________ of numbers. Order is important, so on the coordinate plane, we use the form ( ). The first coordinate represents the point’s location from zero on the ________-axis, and the second coordinate represents the point’s location from zero on the ________-axis.
Answer:
To describe locations of points in the coordinate plane, we use ordered pairs of numbers. Order is important, so on the coordinate plane, we use the form ( x, y ). The first coordinate represents the point’s location from zero on the x -axis, and the second coordinate represents the point’s location from zero on the y -axis.
Eureka Math Grade 6 Module 3 Lesson 15 Exercise Answer Key
Exercise 1.
Use the coordinate plane below to answer parts (a) – (c).
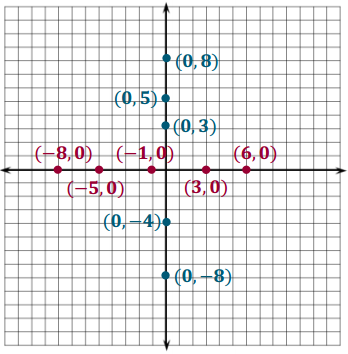
a. Graph at least five points on the x-axis, and label their coordinates.
Answer:
Points will vary.
b. What do the coordinates of your points have in common?
Answer:
Each point has a y-coordinate of 0.
c. What must be true about any point that lies on the x-axis? Explain.
Answer:
If a point lies on the x-axis, its y-coordinate must be 0 because the point is located 0 units above or below the x-axis. The x-axis intersects the y-axis at 0.
Answer:
Exercise 2.
Use the coordinate plane to answer parts (a) – (c).
a. Graph at least five points on the y-axis, and label their coordinates.
Answer:
Points will wary.
b. What do the coordinates of your points have in common?
Answer:
Each point has an x-coordinate of 0.
c. What must be true about any point that lies on the y-axis? Explain.
Answer:
If a point lies on the y-axis, its x-coordinate must be 0 because the point is located 0 units left or right of the y-axis. The y-axis intersects 0 on the x-axis.
Exercise 3.
If the origin is the only point with 0 for both coordinates, what must be true about the origin?
Answer:
The origin is the only point that is on both the x-axis and the y-axis.
Exercise 4.
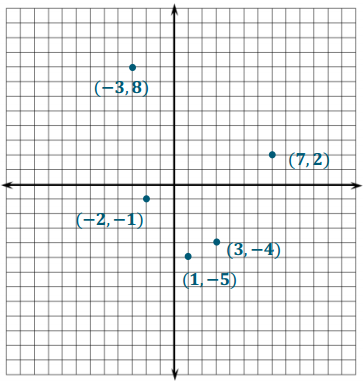
Locate and label each point described by the ordered pairs below. Indicate which of the quadrants the points lie in.
a. (7, 2)
Answer:
Quadrant I
b. (3, – 4)
Answer:
Quadrant IV
c. (1, – 5)
Answer:
Quadrant IV
d. (- 3, 8)
Answer:
Quadrant II
e. (- 2, – 1)
Answer:
Quadrant III
Answer:
Exercise 5.
Write the coordinates of at least one other point in each of the four quadrants.
a. Quadrant I
Answer:
Answers will vary, but both numbers must be positive.
b. Quadrant II
Answer:
Answers will vary, but the x-coordinate must be negative, and the y-coordinate must be positive.
c. Quadrant III
Answer:
Answers will vary, but both numbers must be negative.
d. Quadrant IV
Answer:
Answers will vary, but the x-coordinate must be positive, and the y-coordinate must be negative.
Exercise 6.
Do you see any similarities in the points within each quadrant? Explain your reasoning.
Answer:
The ordered pairs describing the points in Quadrant I contain both positive values. The ordered pairs describing the points in Quadrant III contain both negative values. The first coordinates of the ordered pairs describing the points in Quadrant II are negative values, but their second coordinates are positive values. The first coordinates of the ordered pairs describing the points in Quadrant IV are positive values, but their second coordinates are negative values.
Eureka Math Grade 6 Module 3 Lesson 15 Problem Set Answer Key
Question 1.
Name the quadrant in which each of the points lies. If the point does not lie in a quadrant, specify which axis the point lies on.
a. (- 2, 5)
Quadrant II
b. (8, – 4)
Quadrant IV
c. (- 1, – 8)
Quadrant Ill
d. (9. 2, 7)
Quadrant I
e. (0, – 4)
None; the point is not in a quadrant because it lies on the y-axis.
Question 2.
Jackie claims that points with the same x- and y-coordinates must lie in Quadrant I or Quadrant Ill. Do you agree or disagree? Explain your answer.
Answer:
Disagree; most points with the same x- and y-coordinates lie in Quadrant I or Quadrant III, but the origin (o, 0) is on the x- and y-axes, not in any quadrant.
Question 3.
Locate and label each set of points on the coordinate plane. Describe similarities of the ordered pairs in each set, and describe the points on the plane.
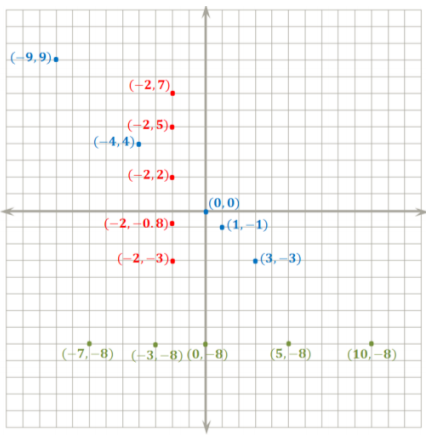
a. {(- 2, 5), (- 2, 2), (- 2, 7), (- 2, – 3), (- 2, – 0. 8))
Answer:
The ordered pairs all have x-coordinates of – 2, and the points lie along a vertical line above and below – 2 on the x-axis.
b. {(- 9, 9), (- 4, 4), (- 2, 2), (1, – 1), (3, – 3), (0, 0)}
Answer:
The ordered pairs each have opposite values for their x- and y-coordinates. The points in the plane line up diagonally through Quadrant II, the origin, and Quadrant IV.
c. {(- 7, – 8), (5, – 8), (0, – 8), (10, – 8), (- 3, – 8)}
Answer:
The ordered pairs all have y-coordinates of – 8, and the points lie along a horizontal line to the left and right of – 8 on the y-axis.
Answer:
Question 4.
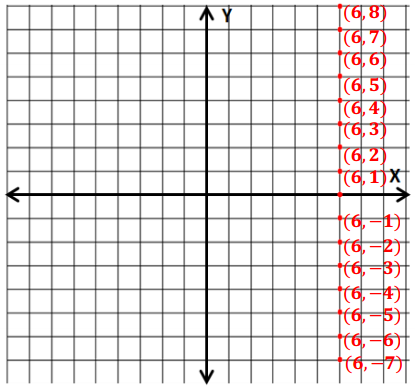
Locate and label at least five points on the coordinate plane that have an x-coordinate of 6.
a. What is true of the y-coordinates below the x-axis?
Answer:
The y-coordinates are all negative values.
b. What is true of the y-coordinates above the x-axis?
Answer:
The y-coordinates are all positive values.
c. What must be true of the y-coordinates on the x-axis?
Answer:
The y-coordinates on the x-axis must be 0.
Answer:
Eureka Math Grade 6 Module 3 Lesson 15 Exit Ticket Answer Key
Question 1.
Label the second quadrant on the coordinate plane, and then answer the following questions:
a. Write the coordinates of one point that lies in the second quadrant of the coordinate plane.
Answer:
Answers will vary.
b. What must be true about the coordinates of any point that lies in the second quadrant?
Answer:
The x-coordinate must be a negative value, and the y-coordinate must be a positive value.
Answer:
Question 2.
Label the third quadrant on the coordinate plane, and then answer the following questions:
a. Write the coordinates of one point that lies in the third quadrant of the coordinate plane.
Answer:
Answers will vary.
b. What must be true about the coordinates of any point that lies in the third quadrant?
Answer:
The x- and y-coordinates of any point in the third quadrant must both be negative values.
Question 3.
An ordered pair has coordinates that have the same sign. In which quadrant(s) could the point lie? Explain.
Answer:
The point would have to be located either in Quadrant I where both coordinates are positive values or in Quadrant III where both coordinates are negative values.
Question 4.
Another ordered pair has coordinates that are opposites. In which quadrant(s) could the point lie? Explain.
Answer:
The point would have to be located in either Quadrant II or Quadrant IV because those are the two quadrants where the coordinates have opposite signs. The point could also be located at the origin (0, 0) since zero is its own opposite.