Engage NY Eureka Math 6th Grade Module 3 Lesson 14 Answer Key
Eureka Math Grade 6 Module 3 Lesson 14 Example Answer Key
Example 1: The Order in Ordered Pairs
The first number of an ordered pair is called the ___________ .
Answer:
first coordinate.
The second number of an ordered pair is called the ___________ .
Answer:
second coordinate.
Example 2.
Using Ordered Pairs to Name Locations
Describe how the ordered pair is being used in your scenario. Indicate what defines the first coordinate and what defines the second coordinate in your scenario.
Answer:
Ordered pairs are like a set of directions; they indicate where to go in one direction and then indicate where to go in the second direction.
→ Scenario 1: The seats in a college football stadium are arranged into 210 sections, with 144 seats in each
section. Your ticket to the game indicates the location of your seat using the ordered pair of numbers
(123,37). Describe the meaning of each number in the ordered pair and how you would use them to find your seat.
→ Scenario 2: Airline pilots use measurements of longitude and latitude to determine their location and to find airports around the world. Longitude is measured as 0 – 180° east or 0 – 180° west of a line stretching from the North Pole to the South Pole through Greenwich, England, called the prime meridian. Latitude is measured as 0 – 90° north or 0 – 90° south of the earth’s equator. A pilot has the ordered pair (90° west, 30° north). What does each number in the ordered pair describe? How would the pilot locate the airport on a map? Would there be any confusion if a pilot were given the ordered pair (90°, 30°)? Explain.
→ Scenario 3: Each room in a school building is named by an ordered pair of numbers that indicates the number of the floor on which the room lies, followed by the sequential number of the room on the floor from the main staircase. A new student at the school is trying to get to science class in room 4 – 13. Describe to the student what each number means and how she should use the number to find her classroom. Suppose there are classrooms below the main floor. How might these rooms be described?
Eureka Math Grade 6 Module 3 Lesson 14 Exercise Answer Key
The first coordinates of the ordered pairs represent the numbers on the line labeled X, and the second coordinates represent the numbers on the line labeled y.
Exercise 1.
Name the letter from the grid below that corresponds with each ordered pair of numbers below.
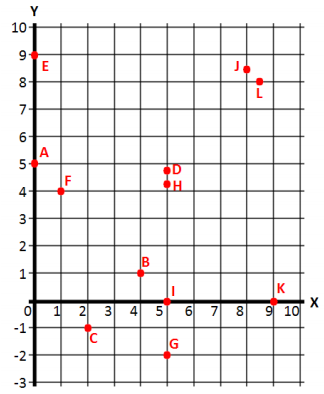
a. (1, 4)
Answer:
Point F
b. (0, 5)
Answer:
Point A
c. (4, 1)
Answer:
Point B
d. (8.5, 8)
Answer:
Point L
e. (5, – 2)
Answer:
Point G
f. (5, 4.2)
Answer:
Point H
g. (2,- 1)
Answer:
Point C
h. (0, 9)
Answer:
Point E
Exercise 2.
List the ordered pair of numbers that corresponds with each letter from the grid below.
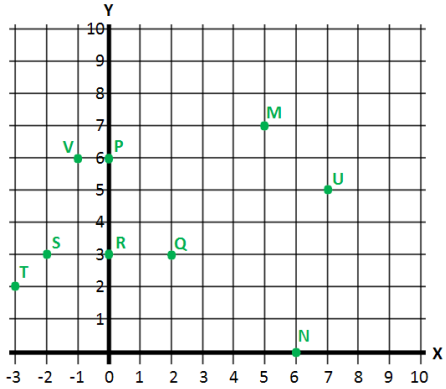
a. Point M
Answer:
(5, 7)
b. Point S
Answer:
(- 2, 3)
c. Point N
Answer:
(6, 0)
d. Point T
Answer:
(- 3, 2)
e. Point P
Answer:
(0, 6)
f. Point U
Answer:
(7, 5)
g. Point Q
Answer:
(2, 3)
h. Point V
Answer:
(- 1, 6)
I. Point R
Answer:
(0, 3)
Eureka Math Grade 6 Module 3 Lesson 14 Problem Set Answer Key
Question 1.
Use the set of ordered pairs below to answer each question.
{(4, 20), (8, 4), (2, 3), (15, 3), (6, 15), (6, 30), (1, 5), (6, 18), (0, 3)}
a. Write the ordered pair(s) whose first and second coordinate have a greatest common factor of 3.
Answer:
(15, 3) and (6, 15)
b. Write the ordered pair(s) whose first coordinate is a factor of its second coordinate.
Answer:
(4, 20), (6, 30), (1, 5), and (6, 18)
c. Write the ordered pair(s) whose second coordinate is a prime number.
Answer:
(2, 3), (15, 3), (1, 5), and (0, 3)
Question 2.
Write ordered pairs that represent the location of points A, B, C, and D, where the first coordinate represents the horizontal direction, and the second coordinate represents the vertical direction.
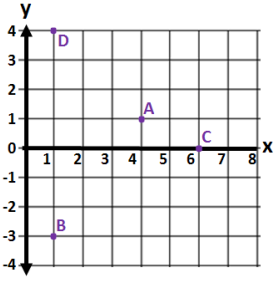
Answer:
A (4, 1); B (1, – 3); C (6, 0); D (1, 4)
Extension:
Question 3.
Write ordered pairs of integers that satisfy the criteria in each part below. Remember that the origin is the point whose coordinates are (0, 0). When possible, give ordered pairs such that (i) both coordinates are positive, (ii) both coordinates are negative, and (iii) the coordinates have opposite signs in either order.
a. These points’ vertical distance from the origin Is twice their horizontal distance.
Answer:
Answers will vary; examples are (5, 10), (- 2, 4), (- 5, – 10), (2, – 4).
b. These points’ horizontal distance from the origin Is two units more than the vertical distance.
Answer:
Answers will vary; examples are (3, 1), (- 3, 1), (- 3,- 1), (3, – 1).
c. These points’ horizontal and vertical distances from the origin are equal, but only one coordinate is positive.
Answer:
Answers will vary; examples are (3, – 3), (- 8,8).
Eureka Math Grade 6 Module 3 Lesson 14 Exit Ticket Answer Key
Question 1.
On the map below, the fire department and the hospital have one matching coordinate. Determine the proper order of the ordered pairs In the map, and write the correct ordered pairs for the locations of the fire department and hospital. Indicate which of their coordinates are the same.
Answer:
The order of the numbers is (x, y); fire department: (6, 7) and hospital: (10, 7); they have the same second coordinate.
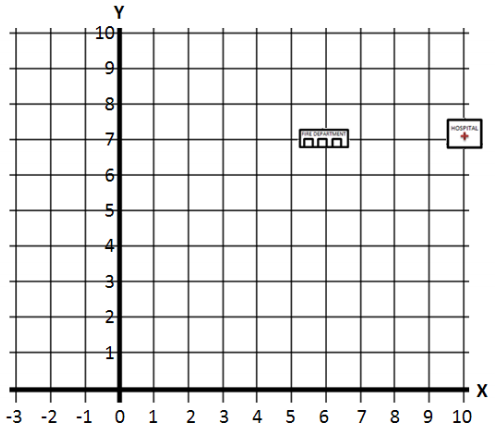
Answer:
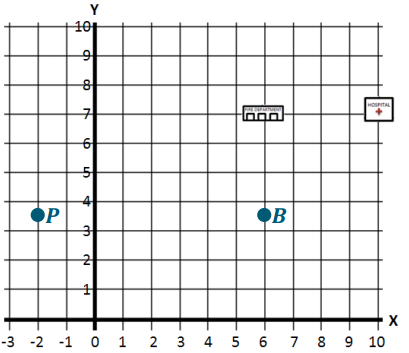
Question 2.
On the map above, locate and label the location of each description below:
a. The local bank has the same first coordinate as the fire department, but its second coordinate is half of the fire department’s second coordinate. What ordered pair describes the location of the bank? Locate and label the bank on the map using point B.
Answer:
(6, 3. 5); see the map image for the correct location of point B.
b. The Village Police Department has the same second coordinate as the bank, but its first coordinate is – 2. What ordered pair describes the location of the Village Police Department? Locate and label the Village Police Department on the map using point P.
Answer:
(- 2, 3.5); see the map image for the correct location of point P.