Engage NY Eureka Math 6th Grade Module 2 Lesson 5 Answer Key
Eureka Math Grade 6 Module 2 Lesson 1 Example Answer Key
Example 1:
\(\frac{1}{2} \div \frac{1}{8}\)
Answer:
Step 1: Decide on an interpretation.
For today, we will only use the measurement interpretation and consider the divisor, 1 eighth, to be the size of the group.
Step 2: Draw a model


Step 3: Find the answer.
\(\frac{1}{2} \div \frac{1}{8}=\frac{4}{8} \div \frac{1}{8}\) = 4 eighths ÷ 1 eighth = 4
So, the answer is 4. There are four \(\frac{1}{8}\) in \(\frac{1}{2}\).
Step 4: Choose a unit.
Answers will vary, but pounds will be used throughout the discussion below.
Step 5: Set up a situation based upon the model.
Answers will vary, but there is a story problem provided in the discussion.
Example 2.
\(\frac{3}{4} \div \frac{1}{2}\)
Answer:
Step 1: Decide on an interpretation.
For today, we’ll only use the measurement interpretation and consider the divisor, 1 half, to be the size of the group.
Step 2: Draw a diagram.
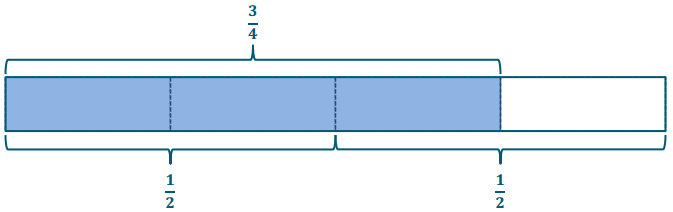
Step 3: Find the answer.
\(\frac{3}{4} \div \frac{1}{2}=\frac{3}{4} \div \frac{2}{4}\) = 3 fourths ÷ 2 fourths = \(\frac{3}{2}\) = 1\(\frac{1}{2}\)
So, the answer is \(\frac{1}{2}\). There are 1\(\frac{1}{2}\) halves in \(\frac{3}{4}\).
Step 4: Choose a unit.
Answers will vary, but ounces will be used throughout the discussion below.
Step 5: Set up a situation based on the model.
Answers will vary, but there is a story problem provided in the discussion.
Eureka Math Grade 6 Module 2 Lesson 1 Exercise Answer Key
Exercise 1.
Using the same dividend and divisor, work with a partner to create your own story problem. You may use the same unit, but your situation must be unique. You could try another unit such as ounces, yards, or miles If you prefer.
Answer:
Possible story problems:
1. Tina uses \(\frac{1}{8}\) oz. of cinnamon each time she makes a batch of coffee cake topping. How many batches can she make if she has \(\frac{1}{2}\)oz. left in her spice jar?
2. Eugenia has \(\frac{1}{2}\) yard of ribbon. For each party decoration, she needs \(\frac{1}{8}\) yard. How many party decorations can she make?
Exercise 2.
Using the same dividend and divisor, work with a partner to create your own story problem. You may use the same unit, but your situation must be unique. You could try another unit such as cups, yards, or miles if you prefer.
Answer:
Possible story problems:
1. Tiffany uses \(\frac{1}{2}\) cup of glycerin each time she makes a batch of soap bubble mixture. How many batches can she make if she has \(\frac{3}{4}\) cup left In her glycerin bottle?
2. Each jug holds \(\frac{3}{4}\) gallon. Each bottle holds \(\frac{1}{2}\) gallon. One jug has the same capacity as how many bottles?
Eureka Math Grade 6 Module 2 Lesson 1 Problem Set Answer Key
Solve.
Question 1.
How many sixteenths are in \(\frac{15}{16}\)?
Answer:
15 sixteenths ÷ 1 sixteenth = 15
There are 15 sixteenths in \(\frac{15}{16}\).
Question 2.
How many \(\frac{1}{4}\) teaspoon doses are in \(\frac{7}{8}\) teaspoon of medicine?
Answer:
7 eighths ÷ 2 eighths = \(\frac{7}{2}\) = 3\(\frac{1}{2}\)
There are 3\(\frac{1}{2}\) doses.
Question 3.
How many cups servings are in a 4 cup container of food?
Answer:
12 thirds ÷ 2 thirds = 6
There are 6 servings in the container.
Question 4.
Write a measurement division story problem for 6 ÷ \(\frac{3}{4}\)
Answer:
Answers will vary.
Question 5
Write a measurement division story problem for \(\frac{5}{12} \div \frac{1}{6}\)
Answer:
Answers will vary.
Question 6.
Fill in the blank to complete the equation. Then, find the quotient, and draw a model to support your solution.
a.
![]()
Answer:
\(\frac{1}{2} \div 5=\frac{1}{5} \text { of } \frac{1}{2}=\frac{1}{10}\)
b.
![]()
Answer:
\(\frac{3}{4} \div 6=\frac{1}{6} \text { of } \frac{3}{4}=\frac{3}{24}\)
Question 7.
\(\frac{4}{5}\) of the money collected from a fund rasier was divided equally among 8 grades. What fraction of the money did each grade receive?
Answer:
\(\frac{4}{5} \div 8=\frac{4}{5} \times \frac{1}{8}=\frac{4}{40}=\frac{1}{10}\)
Each grade got 1 tenth of the money.
Question 8.
Meyer used 6 loads of gravel to cover \(\frac{2}{5}\) of his driveway. How many loads of gravel will he need to cover his entire driveway?
Answer:
6 is \(\frac{2}{5}\) group of what size?
2 units = 6
1 unit = 6 ÷ 2 = 3
5 units = 5 × 3 = 15
Meyer will need 15 loads.
Question 9.
An athlete plans to run 3 miles. Each lap around the school yard is \(\frac{3}{7}\) mile. How many laps will the athlete run?
Answer:
How many \(\frac{3}{7}\) in 3?
21 sevenths ÷ 3 sevenths = 7
The athlete will run 7 laps.
Question 10.
Parks spent \(\frac{1}{3}\) of his money on a sweater. He spent \(\frac{3}{5}\) of the remainder on a pair of jeans. If he has $36 left, how much did the sweater cost?
Answer:
\(\frac{2}{5} \text { of } \frac{2}{3}=\frac{6}{15}\)
\(\frac{1}{3}+\frac{6}{15}=\frac{11}{15}\)
\(\frac{4}{15}\) of Parks’s money is left over.
$36 is \(\frac{4}{15}\) of what number?
4 units = 36
1 unit = 36 ÷ 4 = 9
5 units = 5 × 9 = 45
The sweater cost $45.
Eureka Math Grade 6 Module 2 Lesson 1 Exit Ticket Answer Key
Question 1.
Write a story problem using the measurement interpretation of division for the following: \(\frac{3}{4} \div \frac{1}{8}\) = 6.
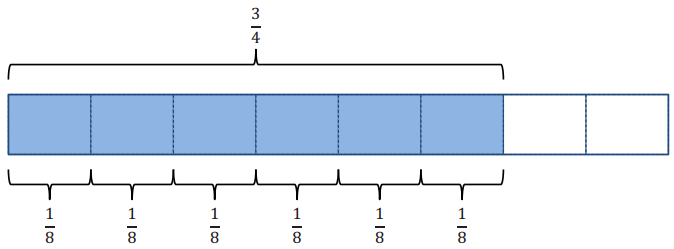
Answer:
Arthur divided \(\frac{3}{4}\) of his kingdom into parcels of land, each being \(\frac{1}{8}\) of the entire kingdom. How many parcels did he make?
(Accept any other reasonable story problem showing \(\frac{3}{4} \div \frac{1}{8}\) = 6.)
Eureka Math Grade 6 Module 2 Lesson 1 Opening Exercise Answer Key
Tape Diagram:
\(\frac{8}{9} \div \frac{2}{9}\)
Answer:
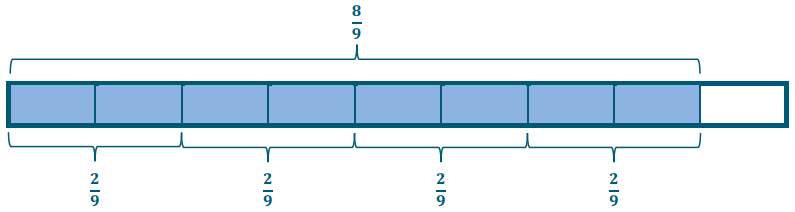
Here we have 4 groups of \(\frac{2}{9}\). Therefore, the answer is 4.
Number Line:
Molly’s friend, Xavier, also has \(\frac{11}{8}\) cups of strawberries. He needs \(\frac{3}{4}\) cup of strawberries to make a batch of tarts. How many batches can he make? Draw a model to support your solution.
Answer:
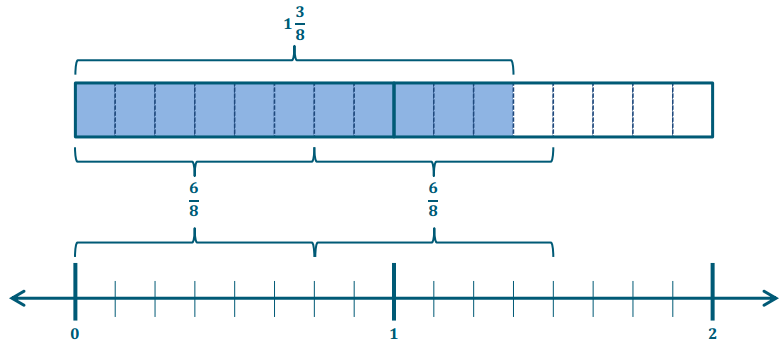
Xavier has enough to make 1 and \(\frac{5}{6}\) batches.