Engage NY Eureka Math 5th Grade Module 4 Lesson 13 Answer Key
Eureka Math Grade 5 Module 4 Lesson 13 Problem Set Answer Key
Solve. Draw a rectangular fraction model to show your thinking. Then, write a multiplication sentence. The first one has been done for you.
a. Half of \(\frac{1}{4}\) pan of brownies = \(\frac{1}{4}\) pan of brownies.
\(\frac{1}{2}\) × \(\frac{1}{4}\) = \(\frac{1}{8}\)
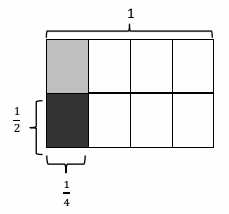
b. Half of \(\frac{1}{3}\) pan of brownies = _____ pan of brownies.
Answer:
\(\frac{1}{6}\) pan of brownies.
Explanation:
Given that there is half of \(\frac{1}{3}\) pan of brownies which is \(\frac{1}{2}\) × \(\frac{1}{3}\) = \(\frac{1}{6}\) pan of brownies.
c. A fourth of \(\frac{1}{3}\) pan of brownies = _____ pan of brownies.
Answer:
\(\frac{1}{12}\) pan of brownies.
Explanation:
Given that there is half of \(\frac{1}{3}\) pan of brownies which is \(\frac{1}{4}\) × \(\frac{1}{3}\) = \(\frac{1}{12}\) pan of brownies.
d. \(\frac{1}{4}\) of \(\frac{1}{4}\)
Answer:
\(\frac{1}{16}\).
Explanation:
Given that \(\frac{1}{4}\) of \(\frac{1}{4}\) which is \(\frac{1}{4}\) × \(\frac{1}{4}\) = \(\frac{1}{16}\).
e. \(\frac{1}{2}\) of \(\frac{1}{6}\)
Answer:
\(\frac{1}{12}\).
Explanation:
Given that \(\frac{1}{2}\) of \(\frac{1}{6}\) which is \(\frac{1}{2}\) × \(\frac{1}{6}\) = \(\frac{1}{12}\).
Question 2.
Draw rectangular fraction models of 3 × \(\frac{1}{4}\) and \(\frac{1}{3}\) × \(\frac{1}{4}\). Compare multiplying a number by 3 and by 1 third.
Answer:
\(\frac{3}{4}\) > \(\frac{1}{12}\).
Explanation:
Given the equations are 3 × \(\frac{1}{4}\) which is \(\frac{3}{4}\) and \(\frac{1}{3}\) × \(\frac{1}{4}\) which is \(\frac{1}{12}\). And \(\frac{3}{4}\) > \(\frac{1}{12}\).
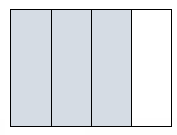
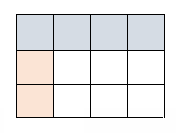
Question 3.
\(\frac{1}{2}\) of Ila’s workspace is covered in paper. \(\frac{1}{3}\) of the paper is covered in yellow sticky notes. What fraction of Ila’s workspace is covered in yellow sticky notes? Draw a picture to support your answer.
Answer:
\(\frac{1}{6}\)
Explanation:
Given that \(\frac{1}{2}\) of Ila’s workspace is covered in paper and \(\frac{1}{3}\) of the paper is covered in yellow sticky notes, so the fraction of Ila’s workspace is covered in yellow sticky notes is \(\frac{1}{2}\) × \(\frac{1}{3}\) which is \(\frac{1}{6}\).
Question 4.
A marching band is rehearsing in rectangular formation. \(\frac{1}{5}\) of the marching band members play percussion instruments. \(\frac{1}{2}\) of the percussionists play the snare drum. What fraction of all the band members play the snare drum?
Answer:
The fraction of all the band members who play the snare drum is \(\frac{1}{10}\).
Explanation:
Given that a \(\frac{1}{5}\) of the marching band members play percussion instruments and \(\frac{1}{2}\) of the percussionists play the snare drum, so the fraction of all the band members play the snare drum is \(\frac{1}{2}\) of \(\frac{1}{5}\) which is \(\frac{1}{2}\) × \(\frac{1}{5}\) = \(\frac{1}{10}\).
Question 5.
Marie is designing a bedspread for her grandson’s new bedroom. \(\frac{2}{3}\) of the bedspread is covered in race cars, and the rest is striped. \(\frac{1}{4}\) of the stripes are red. What fraction of the bedspread is covered in red stripes?
Answer:
The fraction of the bedspread is covered in red stripes is \(\frac{1}{12}\).
Explanation:
Given that \(\frac{2}{3}\) of the bedspread is covered in race cars, and the rest is stripped and \(\frac{1}{4}\) of the stripes are red. The striped bedspread would be 1 – \(\frac{2}{3}\) which is \(\frac{1}{3}\).
So the fraction of the bedspread is covered in red stripes is \(\frac{1}{3}\) × \(\frac{1}{4}\) which is \(\frac{1}{12}\).
Eureka Math Grade 5 Module 4 Lesson 13 Exit Ticket Answer Key
Question 1.
Solve. Draw a rectangular fraction model, and write a number sentence to show your thinking.
\(\frac{1}{3}\) × \(\frac{1}{3}\) =
Answer:
\(\frac{1}{9}\).
Explanation:
Given that \(\frac{1}{3}\) × \(\frac{1}{3}\) which is \(\frac{1}{9}\).
Question 2.
Ms. Sheppard cuts \(\frac{1}{2}\) of a piece of construction paper. She uses \(\frac{1}{6}\) of the piece to make a flower. What fraction of the sheet of paper does she use to make the flower?
Answer:
The fraction of the sheet of paper does she use to make the flower is \(\frac{1}{12}\).
Explanation:
Given that Ms. Sheppard cuts \(\frac{1}{2}\) of a piece of construction paper and she uses \(\frac{1}{6}\) of the piece to make a flower, so the fraction of the sheet of paper does she use to make the flower is \(\frac{1}{2}\) × \(\frac{1}{6}\) which is \(\frac{1}{12}\).
Eureka Math Grade 5 Module 4 Lesson 13 Homework Answer Key
Solve. Draw a rectangular fraction model to show your thinking.
a. Half of \(\frac{1}{2}\) cake = _____ cake.
Answer:
\(\frac{1}{4}\).
Explanation:
Given that half of \(\frac{1}{2}\) cake which is \(\frac{1}{2}\) × \(\frac{1}{2}\) = \(\frac{1}{4}\).
b. One-third of \(\frac{1}{2}\) cake = _____ cake.
Answer:
\(\frac{1}{6}\).
Explanation:
Given that One-third of \(\frac{1}{2}\) cake which is \(\frac{1}{3}\) × \(\frac{1}{2}\) = \(\frac{1}{6}\).
c. \(\frac{1}{4}\) of \(\frac{1}{2}\)
Answer:
\(\frac{1}{8}\).
Explanation:
Given that latex]\frac{1}{4}[/latex] of \(\frac{1}{2}\) which is latex]\frac{1}{4}[/latex] × \(\frac{1}{2}\) = \(\frac{1}{8}\).
d. \(\frac{1}{2}\) × \(\frac{1}{5}\)
Answer:
\(\frac{1}{10}\).
Explanation:
Given that latex]\frac{1}{2}[/latex] of \(\frac{1}{5}\) which is latex]\frac{1}{2}[/latex] × \(\frac{1}{5}\) = \(\frac{1}{10}\).
e. \(\frac{1}{3}\) × \(\frac{1}{3}\)
Answer:
\(\frac{1}{9}\).
Explanation:
Given that latex]\frac{1}{3}[/latex] of \(\frac{1}{3}\) which is latex]\frac{1}{3}[/latex] × \(\frac{1}{3}\) = \(\frac{1}{9}\).
f. \(\frac{1}{4}\) × \(\frac{1}{3}\)
Answer:
\(\frac{1}{12}\).
Explanation:
Given that latex]\frac{1}{4}[/latex] of \(\frac{1}{3}\) which is latex]\frac{1}{4}[/latex] × \(\frac{1}{3}\) = \(\frac{1}{12}\).
Question 2.
Noah mows \(\frac{1}{2}\) of his property and leaves the rest wild. He decides to use \(\frac{1}{5}\) of the wild area for a vegetable garden. What fraction of the property is used for the garden? Draw a picture to support your answer.
Answer:
The fraction of the property is used for the garden is \(\frac{1}{10}\).
Explanation:
Given that Noah mows \(\frac{1}{2}\) of his property and leaves the rest wild and he decides to use \(\frac{1}{5}\) of the wild area for a vegetable garden, so the fraction of the property is used for the garden is \(\frac{1}{2}\) × \(\frac{1}{5}\) which is \(\frac{1}{2}\) × \(\frac{1}{5}\) = \(\frac{1}{10}\).
Question 3.
Fawn plants \(\frac{2}{3}\) of the garden with vegetables. Her son plants the remainder of the garden. He decides to use \(\frac{1}{2}\) of his space to plant flowers, and in the rest, he plants herbs. What fraction of the entire garden is planted in flowers? Draw a picture to support your answer.
Answer:
The fraction of the entire garden is planted in flowers is \(\frac{1}{6}\).
Explanation:
Given that fawn plants \(\frac{2}{3}\) of the garden with vegetables and her son plants the remainder of the garden and he decides to use \(\frac{1}{2}\) of his space to plant flowers, and in the rest, he plants herbs. So her son gets \(\frac{2}{3}\) × \(\frac{1}{2}\) which is \(\frac{1}{3}\). So the fraction of the entire garden is planted in flowers is \(\frac{1}{2}\) × \(\frac{1}{3}\) which is \(\frac{1}{6}\).
Question 4.
Diego eats \(\frac{1}{5}\) of a loaf of bread each day. On Tuesday, Diego eats \(\frac{1}{4}\) of the day’s portion before lunch. What fraction of the whole loaf does Diego eat before lunch on Tuesday? Draw a rectangular fraction model to support your thinking.
Answer:
The fraction of the whole loaf does Diego eat before lunch on Tuesday is \(\frac{1}{20}\).
Explanation:
Given that Diego eats \(\frac{1}{5}\) of a loaf of bread each day and on tuesday, Diego eats \(\frac{1}{4}\) of the day’s portion before lunch. So the fraction of the whole loaf does Diego eat before lunch on Tuesday is \(\frac{1}{5}\) × \(\frac{1}{4}\) which is \(\frac{1}{20}\).