Engage NY Eureka Math 5th Grade Module 4 Lesson 22 Answer Key
Eureka Math Grade 5 Module 4 Lesson 22 Problem Set Answer Key
Question 1.
Solve for the unknown. Rewrite each phrase as a multiplication sentence. Circle the scaling factor and put a box around the number of meters.
a. \(\frac{1}{2}\) as long as 8 meters = ______ meter(s)
Answer:
4 meters.
Explanation:
Given that \(\frac{1}{2}\) as long as 8 meters which is \(\frac{1}{2}\) × 8 = 4 meters.
b. 8 times as long as \(\frac{1}{2}\) meter = _______ meter(s)
Answer:
4 meters.
Explanation:
Given that \(\frac{1}{2}\) meter is 8 times as long, so 8 × \(\frac{1}{2}\) which is 4 meters.
Question 2.
Draw a tape diagram to model each situation in Problem 1, and describe what happened to the number of meters when it was multiplied by the scaling factor.
a.
Answer:
The scaling factor is less than 1, so the number of meters decreases.
Explanation:
The scaling factor is less than 1, so the number of meters decreases.
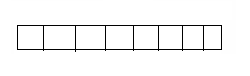
b.
Answer:
The scaling factor is greater than 1, so the number of meters increased.
Explanation:
The scaling factor is greater than 1, so the number of meters increased.

Question 3.
Fill in the blank with a numerator or denominator to make the number sentence true.
a. 7 × \(\frac{}{4}\) < 7
Answer:
7 × \(\frac{}{4}\) < 7.
Explanation:
Given that 7 × \(\frac{}{4}\) < 7, so here in the numerator we will place a number that is less than 4. So we will place 3 in the numerator which will be 7 × \(\frac{3}{4}\) < 7.
b. \(\frac{7}{}\) × 15 > 15
Answer:
\(\frac{7}{2}\) × 15 > 15
Explanation:
Given that \(\frac{7}{2}\) × 15 > 15, so here in the denominator we will place a number that is less than 7. So we will place 2 in the denominator which will be \(\frac{7}{2}\) × 15 > 15.
c. 3 × \(\frac{}{5}\) = 3
Answer:
3 × \(\frac{5}{5}\) = 3
Explanation:
Given that 3 × \(\frac{}{5}\) = 3, so to justify the answer we will place 5 in the numerator which is 3 × \(\frac{5}{5}\) = 3.
Question 4.
Look at the inequalities in each box. Choose a single fraction to write in all three blanks that would make all three number sentences true. Explain how you know.
a. 
Answer:
\(\frac{5}{2}\).
Explanation:

Multiplying by a fraction greater than 1 will make the product larger than the other factor.
b. 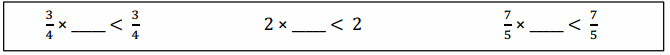
Answer:
\(\frac{1}{2}\).
Explanation:
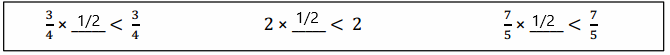
Multiplying by a fraction less than 1 will make the product less than the other factor.
Question 5.
Johnny says multiplication always makes numbers bigger. Explain to Johnny why this isn’t true. Give more than one example to help him understand.
Answer:
4 times 0.5 equals 2.
Explanation:
Given that Johnny says multiplication always makes numbers bigger which is not true because if we multiply any number by a decimal number, we will make it smaller. Because if we multiply a number by something less than one, we will get something less than itself. This also works if you multiply a number by a fraction. For example, 4 times 0.5 equals 2 because you are getting half of the original number which is 4.
Question 6.
A company uses a sketch to plan an advertisement on the side of a building. The lettering on the sketch is \(\frac{3}{4}\) inch tall. In the actual advertisement, the letters must be 34 times as tall. How tall will the letters be on the building?
Answer:
The letters on the building would be 25 \(\frac{1}{2}\) inch.
Explanation:
Given that a company uses a sketch to plan an advertisement on the side of a building and lettering on the sketch is \(\frac{3}{4}\) inch tall and the letters must be 34 times as tall. So to find the height of the building, we will multiply 34 × \(\frac{3}{4}\) inch and the height of the letters on the building which is 34 × \(\frac{3}{4}\) inch
= \(\frac{104}{4}\) inch
= \(\frac{51}{2}\) inch
= 25 \(\frac{1}{2}\) inch.
Therefore the letters on the building would be 25 \(\frac{1}{2}\) inch.
Question 7.
Jason is drawing the floor plan of his bedroom. He is drawing everything with dimensions that are \(\frac{1}{12}\) of the actual size. His bed measures 6 ft by 3 ft, and the room measures 14 ft by 16 ft. What are the dimensions of his bed and room in his drawing?
Answer:
The dimensions of his room in his drawing are 1 \(\frac{1}{3}\) by1 \(\frac{1}{6}\) ft,
The dimensions of his bed in his drawing are \(\frac{1}{2}\) ft by \(\frac{1}{4}\) ft.
Explanation:
Given that Jason is drawing the floor plan of his bedroom and he is drawing everything with dimensions that are \(\frac{1}{12}\) of the actual size and his bed measures 6 ft by 3 ft, and the room measures 14 ft by 16 ft. So the dimensions of his room in his drawing are \(\frac{1}{12}\) of 16 ft and \(\frac{1}{12}\) of 14 ft which is
= \(\frac{1}{12}\) × 16
= \(\frac{4}{3}\)
= 1 \(\frac{1}{3}\)
\(\frac{1}{12}\) of 14 ft
= \(\frac{1}{12}\) × 14 ft
= \(\frac{7}{6}\)
= 1 \(\frac{1}{6}\) ft
So the dimensions of his room in his drawing are 1 \(\frac{1}{3}\) by1 \(\frac{1}{6}\) ft.
For his bed in his drawing are \(\frac{1}{12}\) of 6 ft by \(\frac{1}{12}\) of 3 which is
= \(\frac{1}{12}\) × 6
= \(\frac{1}{2}\) ft
\(\frac{1}{12}\) of 3
= \(\frac{1}{12}\) × 3
= \(\frac{1}{4}\) ft.
So the dimensions of his bed in his drawing are \(\frac{1}{2}\) ft by \(\frac{1}{4}\) ft.
Eureka Math Grade 5 Module 4 Lesson 22 Exit Ticket Answer Key
Fill in the blank to make the number sentences true. Explain how you know.
a. \(\frac{}{3}\) × 11 ˃ 11
Answer:
\(\frac{4}{3}\) × 11 ˃ 11.
Explanation:
Given that \(\frac{}{3}\) × 11 ˃ 11, so here in the numerator we will place a number that is greater than 3. So we will place 4 in the numerator which will be \(\frac{4}{3}\) × 11 ˃ 11.
b. 5 × \(\frac{}{8}\) ˂ 5
Answer:
5 × \(\frac{5}{8}\) ˂ 5.
Explanation:
Given that 5 × \(\frac{}{8}\) ˂ 5, so here in the numerator we will place a number that is less than 8. So we will place 5 in the numerator which will be 5 × \(\frac{5}{8}\) ˂ 5.
c. 6 × \(\frac{2}{}\) = 6
Answer:
6 × \(\frac{2}{2}\) = 6
Explanation:
Given that 6 × \(\frac{2}{2}\) = 6, so to justify the answer we will place 2 in the numerator which is 6 × \(\frac{2}{2}\) = 6
Eureka Math Grade 5 Module 4 Lesson 22 Homework Answer Key
Question 1.
Solve for the unknown. Rewrite each phrase as a multiplication sentence. Circle the scaling factor and put a box around the number of meters.
a. \(\frac{1}{3}\) as long as 6 meters = ______ meter(s)
Answer:
2 meters.
Explanation:
Given that \(\frac{1}{3}\) as long as 6 meters which is \(\frac{1}{3}\) × 6 = 2 meters.
b. 6 times as long as \(\frac{1}{3}\) meter = ______ meter(s)
Answer:
2 meters.
Explanation:
Given that \(\frac{1}{3}\) meter is 6 times as long, so 6 × \(\frac{1}{3}\) which is2 meters.
Question 2.
Draw a tape diagram to model each situation in Problem 1, and describe what happened to the number of meters when it was multiplied by the scaling factor.
a.
Answer:
The scaling factor is less than 1, so the number of meters decreases.
Explanation:
The scaling factor is less than 1, so the number of meters decreases.
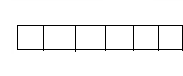
b.
Answer:
The scaling factor is greater than 1, so the number of meters increased.
Explanation:
The scaling factor is greater than 1, so the number of meters increased.
Question 3.
Fill in the blank with a numerator or denominator to make the number sentence true.
a. 5 × \(\frac{}{3}\) ˃ 5
Answer:
5 × \(\frac{2}{3}\) ˃ 5.
Explanation:
Given that 5 × \(\frac{4}{3}\) ˃ 5, so here in the numerator, we will place a number that is greater than 3. So we will place 4 in the numerator which will be 5 × \(\frac{4}{3}\) ˃ 5.
b. \(\frac{6}{}\) × 12 ˂ 12
Answer:
\(\frac{6}{}\) × 12 ˂ 12.
Explanation:
Given that \(\frac{6}{7}\) × 12 ˂ 12, so here in the numerator, we will place a number that is greater than 6. So we will place 7 in the numerator which will be \(\frac{6}{7}\) × 12 ˂ 12.
c. 4 × \(\frac{}{5}\) = 4
Answer:
4 × \(\frac{5}{5}\) = 4
Explanation:
Given that 4 × \(\frac{5}{5}\) = 4, so to justify the answer we will place 5 in the numerator which is 4 × \(\frac{5}{5}\) = 4.
Question 4.
Look at the inequalities in each box. Choose a single fraction to write in all three blanks that would make all three number sentences true. Explain how you know.
a. 
Answer:
\(\frac{5}{4}\).
Explanation:
Multiplying by a fraction greater than 1 will make the product larger than the other factor.
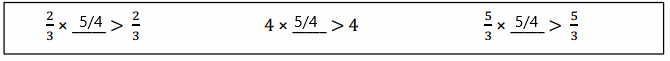
b. 
Answer:
\(\frac{1}{2}\).
Explanation:
Multiplying by a fraction less than 1 will make the product less than the other factor.
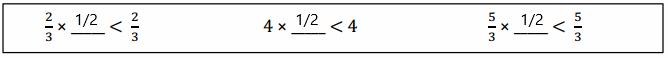
Question 5.
Write a number in the blank that will make the number sentence true.
a. 3 × _____ ˂ 1
Answer:
3 × \(\frac{1}{4}\) < 1.
Explanation:
To make the number sentence true we will place the number which is less than \(\frac{1}{3}\), so we will place \(\frac{1}{4}\) which will be less than 1. So the expression will be 3 × \(\frac{1}{4}\) < 1.
b. Explain how multiplying by a whole number can result in a product less than 1.
Answer:
When a positive whole number is multiplied by a fraction between 0 and 1, the product is less than the whole number. When a number greater than 1 is multiplied by a number greater than 1, the product is greater than both numbers.
Question 6.
In a sketch, a fountain is drawn \(\frac{1}{4}\) yard tall. The actual fountain will be 68 times as tall. How tall will the
fountain be?
Answer:
The actual height of the fountain is 17 yards.
Explanation:
Given that a fountain is drawn \(\frac{1}{4}\) yard tall and the actual fountain will be 68 times as tall. So the actual height of the fountain is \(\frac{1}{4}\) × 68 which is 17 yards.
Question 7.
In blueprints, an architect’s firm drew everything \(\frac{1}{24}\) of the actual size. The windows will actually measure 4 ft by 6 ft and doors measure 12 ft by 8 ft. What are the dimensions of the windows and the doors in the drawing?
Answer:
The dimensions of the windows are 2 in by 3 in.
The dimensions of the windows are 6 in by 4 in.
Explanation:
Given that an architect’s firm drew everything \(\frac{1}{24}\) of the actual size and the windows will actually measure 4 ft by 6 ft, so the dimensions of the length of the windows are \(\frac{1}{24}\) × 4 which is \(\frac{1}{6}\) ft, so in inch, it will be \(\frac{1}{6}\) × 12 which is 2 in. And the width of the windows is \(\frac{1}{24}\) × 6 which is \(\frac{1}{4}\), so in inch, it will be \(\frac{1}{4}\) × 12 which is 3 in. So the dimensions of the windows are 2 in by 3 in. Given that the measures of the door are 12 ft by 8 ft, so the dimensions of the length of the doors are \(\frac{1}{24}\) × 12 which is \(\frac{1}{2}\) ft, so in inch, it will be \(\frac{1}{2}\) × 12 which is 6 in. And the width of the windows is \(\frac{1}{24}\) × 8 which is \(\frac{1}{3}\), so in inch, it will be \(\frac{1}{3}\) × 12 which is 4 in.